題目連結：http://acm.hdu.edu.cn/showproblem.php?pid=3157

You’ve just built a circuit board for your new robot, and now you need to power it. Your robot circuit consists of a number of electrical components that each require a certain amount of current to operate. Every component has a + and a - lead, which are connected on the circuit board at junctions. Current flows through the component from + to - (but note that a component does not "use up" the current: everything that comes in through the + end goes out the - end). The junctions on the board are labeled 1, ..., N , except for two special junctions labeled + and - where the power supply terminals are connected. The + terminal only connects + leads, and the - terminal only connects - leads. All current that enters a junction from the - leads of connected components exits through connected + leads, but you are able to control how much current flows to each connected + lead at every junction (though methods for doing so are beyond the scope of this problem1). Moreover, you know you have assembled the circuit in such a way that there are no feedback loops (components chained in a manner that allows current to flow in a loop).   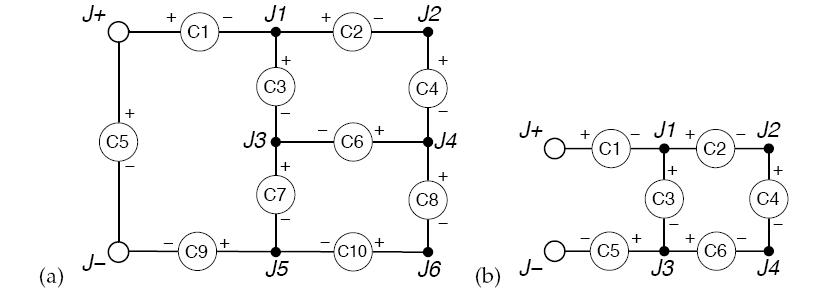Figure 1: Examples of two valid circuit diagrams. In (a), all components can be powered along directed paths from the positive terminal to the negative terminal. In (b), components 4 and 6 cannot be powered, since there is no directed path from junction 4 to the negative terminal. In the interest of saving power, and also to ensure that your circuit does not overheat, you would like to use as little current as possible to get your robot to work. What is the smallest amount of current that you need to put through the + terminal (which you can imagine all necessarily leaving through the - terminal) so that every component on your robot receives its required supply of current to function? Hint 1 For those who are electronics-inclined, imagine that you have the ability to adjust the potential on any componentwithout altering its current requirement, or equivalently that there is an accurate variable potentiometer connected in series with each component that you can adjust. Your power supply will have ample potential for the circuit.     Input The input file will contain multiple test cases. Each test case begins with a single line containing two integers: N (0 <= N <= 50), the number of junctions not including the positive and negative terminals, and M (1 <= M <= 200), the number of components in the circuit diagram. The next M lines each contain a description of some component in the diagram. The ith component description contains three fields: pi, the positive junction to which the component is connected, ni, the negative junction to which the component is connected, and an integer Ii (1 <= Ii <= 100), the minimum amount of current required for component i to function. The junctions pi and ni are specified as either the character '+' indicating the positive terminal, the character '-' indicating the negative terminal, or an integer (between 1 and N) indicating one of the numbered junctions. No two components have the same positive junction and the same negative junction. The end-of-file is denoted by an invalid test case with N = M = 0 and should not be processed.     Output For each input test case, your program should print out either a single integer indicating the minimum amount of current that must be supplied at the positive terminal in order to ensure that every component is powered, or the message "impossible" if there is no way to direct a sufficient amount of current to each component simultaneously.     Sample Input   6 10 + 1 1 1 2 1 1 3 2 2 4 5 + - 1 4 3 2 3 5 5 4 6 2 5 - 1 6 5 3 4 6 + 1 8 1 2 4 1 3 5 2 4 6 3 - 1 3 4 3 0 0     Sample Output   9 impossible

 

題意：有兩個正負極n個節點和m個元件，每個元件告訴端點是接在哪個節點上的，並且每個元件有工作的最小電流限制，問使所有元件工作的滿足條件的最小電流是多少。

流量有上下限的有源匯的最小流建圖：

1.u到v建容量為C[u,v]-B[u.v]的邊 //C是上界，B是下界
2.對於點u,記tmp為in[u]-ou[u],若tmp>0，則S向u建容量為tmp的邊，若tmp<0，則u向T建邊，容量是-tmp。//in[u]記錄u的入邊的流量下界和，ou[u]記錄u的出邊的流量的下界和

先跑一遍最大流，然後源點和匯點連一條容量為inf的邊，再跑一遍最大流，就是解

#pragma GCC optimize(2)
#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<set>
#include<vector>
#include<string>
#include<queue>
using namespace std;
const int maxn = 5005;
const int inf = 0x3f3f3f3f;
typedef long long ll;
int node, src, dest, edge;
int ver[maxn], flow[maxn], _next[maxn];
int head[maxn], work[maxn], dis[maxn], q[maxn], in[maxn];
void init(int _node, int _src, int _dest)
{
	node = _node, src = _src, dest = _dest;
	for (int i = 0; i < node; ++i)
	{
		head[i] = -1, in[i] = 0;
	}
	edge = 0;
}
void addedge(int u, int v, int c)
{
	ver[edge] = v, flow[edge] = c, _next[edge] = head[u], head[u] = edge++;
	ver[edge] = u, flow[edge] = 0, _next[edge] = head[v], head[v] = edge++;
}
bool Dinic_bfs()
{
	int i, u, v, l, r = 0;
	memset(dis, -1, sizeof(dis));
	queue<int>pq;
	dis[src] = 0;
	pq.push(src);
	while (!pq.empty())
	{
		int u = pq.front();
		pq.pop();
		for (i = head[u]; i >= 0; i = _next[i])
		{
			int v = ver[i];
			if (flow[i] && dis[v] < 0)
			{
				dis[v] = dis[u] + 1;
				pq.push(v);
				if (v == dest)
				{
					return 1;
				}
			}
		}
	}
	return 0;
}
int Dinic_dfs(int u, int f)
{
	if (u == dest)
	{
		return f;
	}
	int v, tmp;
	for (int &i = work[u]; i >= 0; i = _next[i])
	{
		v = ver[i];
		if (flow[i] && dis[v] == dis[u] + 1)
		{
			tmp = Dinic_dfs(v, min(f, flow[i]));
			if (tmp > 0)
			{
				flow[i] -= tmp;
				flow[i ^ 1] += tmp;
				return tmp;
			}
		}
	}
	return 0;
}
void Dinic_flow()
{
	while (Dinic_bfs())
	{
		for (int i = 0; i < node; ++i)
		{
			work[i] = head[i];
		}
		while (Dinic_dfs(src, inf));
	}
}
int Limit_flow()
{
	int i, src0, dest0;
	src0 = src, dest0 = dest;
	src = node++, dest = node++;
	head[src] = head[dest] = -1;
	for (i = 0; i < node - 2; ++i)
	{
		if (in[i] > 0)addedge(src, i, in[i]);
		if (in[i] < 0)addedge(i, dest, -in[i]);
	}
	Dinic_flow();
	addedge(dest0, src0, inf);
	Dinic_flow();
	for (i = head[src]; i >= 0; i = _next[i])
		if (flow[i])return -1;
	for (i = head[dest0]; i >= 0; i = _next[i])
		if (ver[i] == src0)return flow[i ^ 1];
	return 0;
}
void get(int &a)
{
	char c;
	while (((c = getchar()) < '0' || c > '9') && c != '-'&&c != '+');
	if (c == '-') { a = dest; return; }
	if (c == '+') { a = src; return; }
	for (a = 0; c >= '0'&&c <= '9'; c = getchar())a = a * 10 + c - '0';
}
int main()
{
	//freopen("C:/input.txt", "r", stdin);
	int u, v, c, n, m, ans;
	while (get(n), get(m), n + m)
	{
		init(n + 2, 0, n + 1);
		while (m--)
		{
			get(u), get(v), get(c);
			in[u] -= c;
			in[v] += c;
			addedge(u, v, inf);
		}
		if ((ans = Limit_flow()) >= 0)
		{
			printf("%d\n", ans);
		}
		else 
			printf("impossible\n");
	}
}