PCL ——最小包圍盒(畫出了最小包圍盒並求出頂點座標)
PCL ——最小包圍盒
2018年09月21日 15:31:01 不懂音樂的欣賞者 閱讀數:35 標籤: PCL包圍盒外接矩形最小矩形收起
個人分類: PCL
1.包圍盒簡介
包圍盒也叫外接最小矩形,是一種求解離散點集最優包圍空間的演算法,基本思想是用體積稍大且特性簡單的幾何體(稱為包圍盒)來近似地代替複雜的幾何物件。
常見的包圍盒演算法有AABB包圍盒、包圍球、方向包圍盒OBB以及固定方向凸包FDH。碰撞檢測問題在虛擬現實、計算機輔助設計與製造、遊戲及機器人等領域有著廣泛的應用,甚至成為關鍵技術。而包圍盒演算法是進行碰撞干涉初步檢測的重要方法之一。
在此藉助於PCL點雲庫尋找點雲的最小包圍盒,程式碼參考網上程式碼,因為工程需要包圍盒的頂點座標或偏轉角度,網上程式碼都只畫出了最小包圍盒沒有求出頂點座標,所以自己折騰了很久終於把頂點座標求出,下面將程式碼放出來供大家參考.
2.原理簡述
最小包圍盒的計算過程大致如下:
1.利用PCA主元分析法獲得點雲的三個主方向,獲取質心,計算協方差,獲得協方差矩陣,求取協方差矩陣的特徵值和特長向量,特徵向量即為主方向。
2.利用1中獲得的主方向和質心,將輸入點雲轉換至原點,且主方向與座標系方向重回,建立變換到原點的點雲的包圍盒。
3.給輸入點雲設定主方向和包圍盒,通過輸入點雲到原點點雲變換的逆變換實現。
最小包圍盒頂點計算的過程大致如下:
1.輸入點雲轉換至遠點後,求得變換後點雲的最大最小x,y,z軸的座標,此時(max.x,max.y,max.z),(max.x,min.y,max.z),(max.x,max.y,min.z),(min.x,max.y,max.z),(min.x,max.y,min.z),(min.x,min.y,max.z),(min.x,min.y,max.z),(min.x,min.y,min.z)
即為變換後點雲的包圍盒,也是原始輸入點雲包圍盒頂點座標經過變化後的座標.
2.將上述求得的6個包圍盒座標逆變換回輸入點雲的座標系,即得到原始輸入點雲的包圍盒頂點座標.
3.詳細程式碼
#include <iostream>
#include <pcl/ModelCoefficients.h>
#include <pcl/io/pcd_io.h>
#include <pcl/filters/project_inliers.h>
#include <pcl/filters/extract_indices.h>
#include <pcl/sample_consensus/method_types.h>
#include <pcl/sample_consensus/model_types.h>
#include <pcl/segmentation/sac_segmentation.h>
#include <pcl/visualization/cloud_viewer.h>
#include <pcl/point_types.h>
#include <pcl/filters/voxel_grid.h>
#include <pcl/filters/passthrough.h>
#include <pcl/features/normal_3d.h>
#include <pcl/filters/radius_outlier_removal.h>
#include <pcl/kdtree/kdtree_flann.h>
#include <pcl/segmentation/extract_clusters.h>
#include <Eigen/Core>
#include <pcl/common/transforms.h>
#include <pcl/common/common.h>
#include <pcl/common/time.h>
#include <pcl/common/angles.h>
#include <pcl/registration/transformation_estimation_svd.h>
using namespace std;
typedef pcl::PointXYZ PointType;
typedef struct myPointType
{
double x; //mm world coordinate x
double y; //mm world coordinate y
double z; //mm world coordinate z
int num; //point num
};
// Get N bits of the string from back to front.
char* Substrend(char*str,int n)
{
char *substr=(char*)malloc(n+1);
int length=strlen(str);
if (n>=length)
{
strcpy(substr,str);
return substr;
}
int k=0;
for (int i=length-n;i<length;i++)
{
substr[k]=str[i];
k++;
}
substr[k]='\0';
return substr;
}
int main(int argc, char **argv)
{
// create point cloud
pcl::PointCloud<PointType>::Ptr cloud(new pcl::PointCloud<PointType>());
// load data
char* fileType;
if (argc>1)
{
fileType = Substrend(argv[1],3);
}
if (!strcmp(fileType,"pcd"))
{
// load pcd file
pcl::io::loadPCDFile(argv[1], *cloud);
}
else if(!strcmp(fileType,"txt"))
{
// load txt data file
int number_Txt;
myPointType txtPoint;
vector<myPointType> points;
FILE *fp_txt;
fp_txt = fopen(argv[1], "r");
if (fp_txt)
{
while (fscanf(fp_txt, "%lf %lf %lf", &txtPoint.x, &txtPoint.y, &txtPoint.z) != EOF)
{
points.push_back(txtPoint);
}
}
else
std::cout << "txt資料載入失敗!" << endl;
number_Txt = points.size();
cloud->width = number_Txt;
cloud->height = 1;
cloud->is_dense = false;
cloud->points.resize(cloud->width * cloud->height);
for (size_t i = 0; i < cloud->points.size(); ++i)
{
cloud->points[i].x = points[i].x;
cloud->points[i].y = points[i].y;
cloud->points[i].z = 0;
}
}
else
{
std::cout << "please input data file name"<<endl;
return 0;
}
// start calculating time
pcl::StopWatch time;
Eigen::Vector4f pcaCentroid;
pcl::compute3DCentroid(*cloud, pcaCentroid);
Eigen::Matrix3f covariance;
pcl::computeCovarianceMatrixNormalized(*cloud, pcaCentroid, covariance);
Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> eigen_solver(covariance, Eigen::ComputeEigenvectors);
Eigen::Matrix3f eigenVectorsPCA = eigen_solver.eigenvectors();
Eigen::Vector3f eigenValuesPCA = eigen_solver.eigenvalues();
eigenVectorsPCA.col(2) = eigenVectorsPCA.col(0).cross(eigenVectorsPCA.col(1)); //校正主方向間垂直
eigenVectorsPCA.col(0) = eigenVectorsPCA.col(1).cross(eigenVectorsPCA.col(2));
eigenVectorsPCA.col(1) = eigenVectorsPCA.col(2).cross(eigenVectorsPCA.col(0));
std::cout << "特徵值va(3x1):\n" << eigenValuesPCA << std::endl;
std::cout << "特徵向量ve(3x3):\n" << eigenVectorsPCA << std::endl;
std::cout << "質心點(4x1):\n" << pcaCentroid << std::endl;
/*
// 另一種計算點雲協方差矩陣特徵值和特徵向量的方式:通過pcl中的pca介面,如下,這種情況得到的特徵向量相似特徵向量
pcl::PointCloud<pcl::PointXYZ>::Ptr cloudPCAprojection (new pcl::PointCloud<pcl::PointXYZ>);
pcl::PCA<pcl::PointXYZ> pca;
pca.setInputCloud(cloudSegmented);
pca.project(*cloudSegmented, *cloudPCAprojection);
std::cerr << std::endl << "EigenVectors: " << pca.getEigenVectors() << std::endl;//計算特徵向量
std::cerr << std::endl << "EigenValues: " << pca.getEigenValues() << std::endl;//計算特徵值
*/
Eigen::Matrix4f tm = Eigen::Matrix4f::Identity();
Eigen::Matrix4f tm_inv = Eigen::Matrix4f::Identity();
tm.block<3, 3>(0, 0) = eigenVectorsPCA.transpose(); //R.
tm.block<3, 1>(0, 3) = -1.0f * (eigenVectorsPCA.transpose()) *(pcaCentroid.head<3>());// -R*t
tm_inv = tm.inverse();
std::cout << "變換矩陣tm(4x4):\n" << tm << std::endl;
std::cout << "逆變矩陣tm'(4x4):\n" << tm_inv << std::endl;
pcl::PointCloud<PointType>::Ptr transformedCloud(new pcl::PointCloud<PointType>);
pcl::transformPointCloud(*cloud, *transformedCloud, tm);
PointType min_p1, max_p1;
Eigen::Vector3f c1, c;
pcl::getMinMax3D(*transformedCloud, min_p1, max_p1);
c1 = 0.5f*(min_p1.getVector3fMap() + max_p1.getVector3fMap());
std::cout << "型心c1(3x1):\n" << c1 << std::endl;
Eigen::Affine3f tm_inv_aff(tm_inv);
pcl::transformPoint(c1, c, tm_inv_aff);
Eigen::Vector3f whd, whd1;
whd1 = max_p1.getVector3fMap() - min_p1.getVector3fMap();
whd = whd1;
float sc1 = (whd1(0) + whd1(1) + whd1(2)) / 3; //點雲平均尺度,用於設定主方向箭頭大小
std::cout << "width1=" << whd1(0) << endl;
std::cout << "heght1=" << whd1(1) << endl;
std::cout << "depth1=" << whd1(2) << endl;
std::cout << "scale1=" << sc1 << endl;
const Eigen::Quaternionf bboxQ1(Eigen::Quaternionf::Identity());
const Eigen::Vector3f bboxT1(c1);
const Eigen::Quaternionf bboxQ(tm_inv.block<3, 3>(0, 0));
const Eigen::Vector3f bboxT(c);
//變換到原點的點雲主方向
PointType op;
op.x = 0.0;
op.y = 0.0;
op.z = 0.0;
Eigen::Vector3f px, py, pz;
Eigen::Affine3f tm_aff(tm);
pcl::transformVector(eigenVectorsPCA.col(0), px, tm_aff);
pcl::transformVector(eigenVectorsPCA.col(1), py, tm_aff);
pcl::transformVector(eigenVectorsPCA.col(2), pz, tm_aff);
PointType pcaX;
pcaX.x = sc1 * px(0);
pcaX.y = sc1 * px(1);
pcaX.z = sc1 * px(2);
PointType pcaY;
pcaY.x = sc1 * py(0);
pcaY.y = sc1 * py(1);
pcaY.z = sc1 * py(2);
PointType pcaZ;
pcaZ.x = sc1 * pz(0);
pcaZ.y = sc1 * pz(1);
pcaZ.z = sc1 * pz(2);
//初始點雲的主方向
PointType cp;
cp.x = pcaCentroid(0);
cp.y = pcaCentroid(1);
cp.z = pcaCentroid(2);
PointType pcX;
pcX.x = sc1 * eigenVectorsPCA(0, 0) + cp.x;
pcX.y = sc1 * eigenVectorsPCA(1, 0) + cp.y;
pcX.z = sc1 * eigenVectorsPCA(2, 0) + cp.z;
PointType pcY;
pcY.x = sc1 * eigenVectorsPCA(0, 1) + cp.x;
pcY.y = sc1 * eigenVectorsPCA(1, 1) + cp.y;
pcY.z = sc1 * eigenVectorsPCA(2, 1) + cp.z;
PointType pcZ;
pcZ.x = sc1 * eigenVectorsPCA(0, 2) + cp.x;
pcZ.y = sc1 * eigenVectorsPCA(1, 2) + cp.y;
pcZ.z = sc1 * eigenVectorsPCA(2, 2) + cp.z;
//Rectangular vertex
pcl::PointCloud<PointType>::Ptr transVertexCloud(new pcl::PointCloud<PointType>);//存放變換後點雲包圍盒的6個頂點
pcl::PointCloud<PointType>::Ptr VertexCloud(new pcl::PointCloud<PointType>);//存放原來點雲中包圍盒的6個頂點
transVertexCloud->width = 6;
transVertexCloud->height = 1;
transVertexCloud->is_dense = false;
transVertexCloud->points.resize(transVertexCloud->width * transVertexCloud->height);
transVertexCloud->points[0].x = max_p1.x;
transVertexCloud->points[0].y = max_p1.y;
transVertexCloud->points[0].z = max_p1.z;
transVertexCloud->points[1].x = max_p1.x;
transVertexCloud->points[1].y = max_p1.y;
transVertexCloud->points[1].z = min_p1.z;
transVertexCloud->points[2].x = max_p1.x;
transVertexCloud->points[2].y = min_p1.y;
transVertexCloud->points[2].z = min_p1.z;
transVertexCloud->points[3].x = min_p1.x;
transVertexCloud->points[3].y = max_p1.y;
transVertexCloud->points[3].z = max_p1.z;
transVertexCloud->points[4].x = min_p1.x;
transVertexCloud->points[4].y = min_p1.y;
transVertexCloud->points[4].z = max_p1.z;
transVertexCloud->points[5].x = min_p1.x;
transVertexCloud->points[5].y = min_p1.y;
transVertexCloud->points[5].z = min_p1.z;
pcl::transformPointCloud(*transVertexCloud, *VertexCloud, tm_inv);
// 逆變換回來的角度
cout << whd1(0) << " "<< whd1(1) << " " << whd1(2) << endl;
auto euler = bboxQ1.toRotationMatrix().eulerAngles(0, 1, 2);
std::cout << "Euler from quaternion in roll, pitch, yaw"<< std::endl << euler/3.14*180 << std::endl<<std::endl;
//Output time consumption
std::cout << "執行時間" << time.getTime() << "ms" << std::endl;
//visualization
pcl::visualization::PCLVisualizer viewer;
pcl::visualization::PointCloudColorHandlerCustom<PointType> tc_handler(transformedCloud, 0, 255, 0); //設定點雲顏色
//Visual transformed point cloud
viewer.addPointCloud(transformedCloud, tc_handler, "transformCloud");
viewer.addCube(bboxT1, bboxQ1, whd1(0), whd1(1), whd1(2), "bbox1");
viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, "bbox1");
viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 0.0, 1.0, 0.0, "bbox1");
viewer.addArrow(pcaX, op, 1.0, 0.0, 0.0, false, "arrow_X");
viewer.addArrow(pcaY, op, 0.0, 1.0, 0.0, false, "arrow_Y");
viewer.addArrow(pcaZ, op, 0.0, 0.0, 1.0, false, "arrow_Z");
pcl::visualization::PointCloudColorHandlerCustom<PointType> color_handler(cloud, 255, 0, 0);
viewer.addPointCloud(cloud, color_handler, "cloud");
viewer.addCube(bboxT, bboxQ, whd(0), whd(1), whd(2), "bbox");
viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_REPRESENTATION, pcl::visualization::PCL_VISUALIZER_REPRESENTATION_WIREFRAME, "bbox");
viewer.setShapeRenderingProperties(pcl::visualization::PCL_VISUALIZER_COLOR, 1.0, 0.0, 0.0, "bbox");
viewer.addArrow(pcX, cp, 1.0, 0.0, 0.0, false, "arrow_x");
viewer.addArrow(pcY, cp, 0.0, 1.0, 0.0, false, "arrow_y");
viewer.addArrow(pcZ, cp, 0.0, 0.0, 1.0, false, "arrow_z");
viewer.addCoordinateSystem(0.5f*sc1);
viewer.setBackgroundColor(0.0, 0.0, 0.0);
viewer.addPointCloud(VertexCloud, "temp_cloud");
viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 10, "temp_cloud");
while (!viewer.wasStopped())
{
viewer.spinOnce();
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221
- 222
- 223
- 224
- 225
- 226
- 227
- 228
- 229
- 230
- 231
- 232
- 233
- 234
- 235
- 236
- 237
- 238
- 239
- 240
- 241
- 242
- 243
- 244
- 245
- 246
- 247
- 248
- 249
- 250
- 251
- 252
- 253
- 254
- 255
- 256
- 257
- 258
- 259
- 260
- 261
- 262
- 263
- 264
- 265
- 266
- 267
- 268
- 269
- 270
- 271
- 272
- 273
- 274
- 275
- 276
- 277
- 278
- 279
- 280
- 281
- 282
- 283
4.程式碼編譯
在次使用的是CMake編譯,因此需要新增CMakeLists.txt檔案後才可以進行編譯
mkdir build
cd build
cmake ..
make
- 1
- 2
- 3
- 4
5.執行
執行時記得在後面加上點雲檔案的名字,程式碼裡面支援’.pcd’格式和’.txt’格式,其它格式需要自己編寫讀取程式碼.’.txt’格式的檔案中點雲格式如下,一行代表一個點的座標,橫軸、縱軸、豎軸座標之間加空格隔開:
point1.x point1.y point1.z
point2.x point2.y point2.z
...
pointN.x pointN.y pointN.z
- 1
- 2
- 3
- 4
執行命令如下
./rectangular_bounding_box ../milk.pcd
- 1
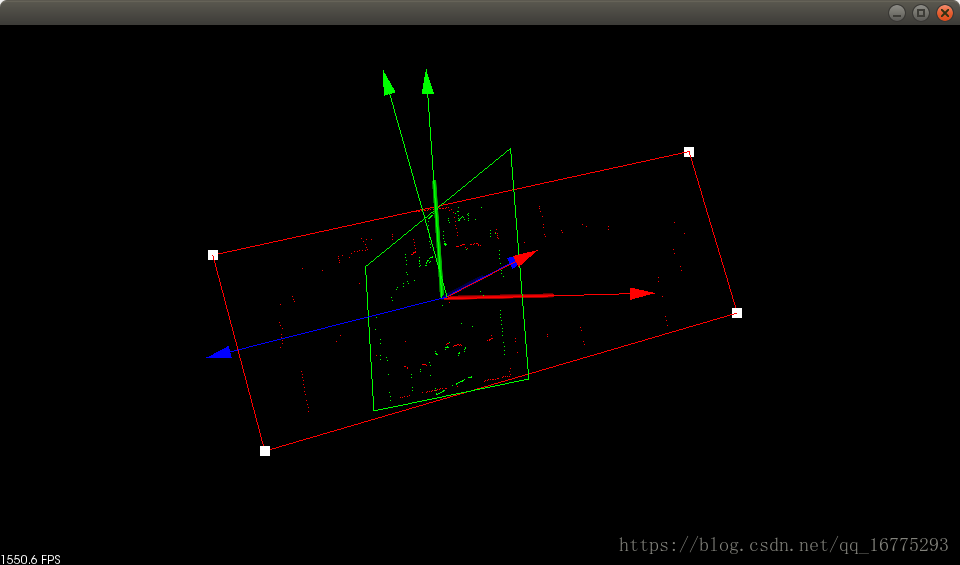
6.效果圖
2維點雲包圍盒效果圖
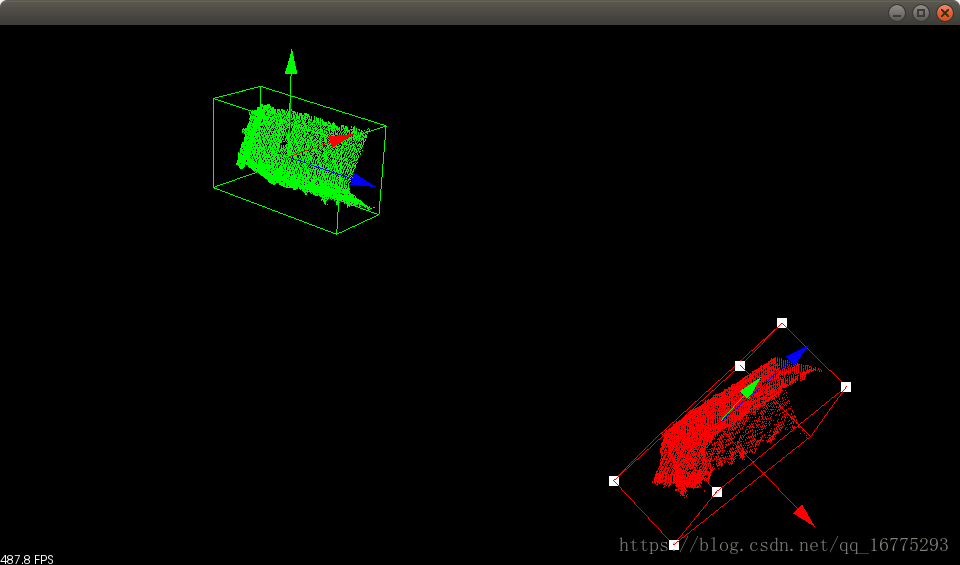
3維點雲包圍盒效果圖
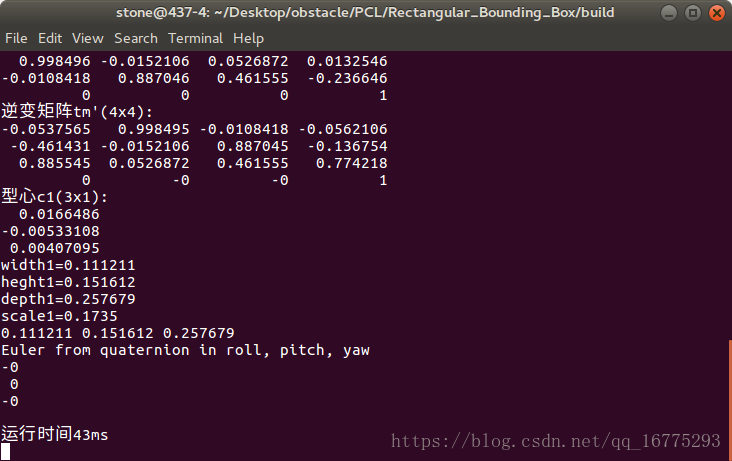
3維點雲包圍盒執行時間圖
7.完整程式碼下載
如果不想自己寫“CMakeLists.txt”的朋友可以下完整的程式碼,點選這裡下載,包括“.cpp”檔案,“CMakeLists.txt”檔案。
參考:https://blog.csdn.net/qq_16775293/article/details/82801240