[Reinforcement Learning] Model-Free Prediction
上篇文章介紹了 Model-based 的通用方法——動態規劃,本文內容介紹 Model-Free 情況下 Prediction 問題,即 "Estimate the value function of an unknown MDP"。
- Model-based:MDP已知,即轉移矩陣和獎賞函式均已知
- Model-Free:MDP未知
蒙特卡洛學習
蒙特卡洛方法(Monte-Carlo Methods,簡稱MC)也叫做蒙特卡洛模擬,是指使用隨機數(或更常見的偽隨機數)來解決很多計算問題的方法。其實本質就是,通過儘可能隨機的行為產生後驗,然後通過後驗來表徵目標系統。
如下圖為使用蒙特卡羅方法估算 \(\pi\)
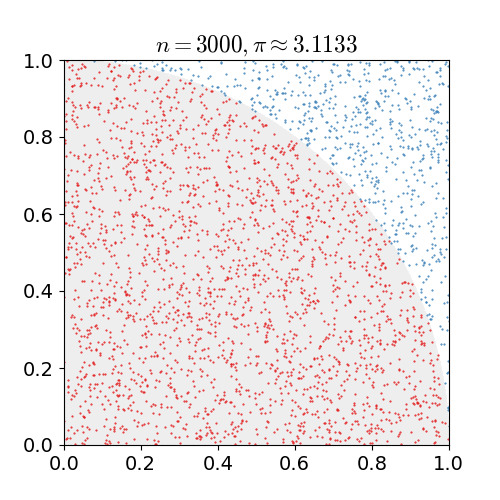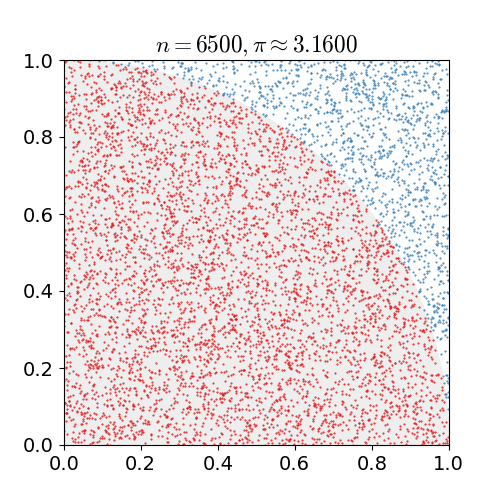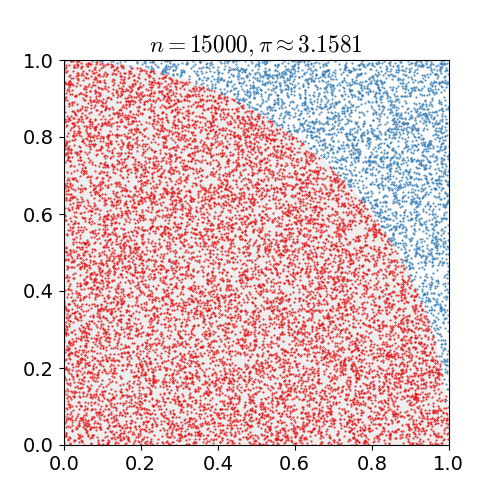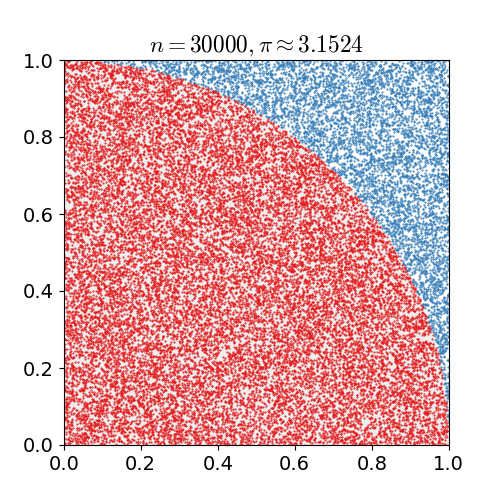
在Model-Free的情況下,MC在強化學習中的應用就是獲取價值函式,其特點如下:
- MC 可以從完整的 episodes 中學習(no bootstrapping)
- MC 以均值來計算價值,即 value = mean(return)
- MC 只能適用於 episodic MDPs(有限MDPs)
First-Visit 蒙特卡洛策略評估
First-Visit Monte-Carlo Policy Evaluation:
評估狀態 \(s\) 在給定策略 \(\pi\)
下的價值函式 \(v_{\pi}(s)\) 時,在一次 episode 中,狀態 \(s\) 在時刻 \(t\) 第一次被訪問時,計數器 \(N(s) ← N(s) + 1\),累計價值 \(S(s) ← S(s) + G_t\)
當整個過程結束後,狀態 \(s\) 的價值 \(V(s) = \frac{S(s)}{N(s)}\)
根據大數定理(Law of Large Numbers):\(V(s) → v_{\pi}(s) \text{ as } N(s) → \infty\)
Every-Visit 蒙特卡洛策略評估
Every-Visit Monte-Carlo Policy Evaluation:
評估狀態 \(s\) 在給定策略 \(\pi\) 下的價值函式 \(v_{\pi}(s)\) 時,在一次 episode 中,狀態 \(s\) 在時刻 \(t\) 每次被訪問時,計數器 \(N(s) ← N(s) + 1\),累計價值 \(S(s) ← S(s) + G_t\)
當整個過程結束後,狀態 \(s\) 的價值 \(V(s) = \frac{S(s)}{N(s)}\)
根據大數定理(Law of Large Numbers):\(V(s) → v_{\pi}(s) \text{ as } N(s) → \infty\)
Incremental Monte-Carlo
我們先看下增量式求平均:
The mean \(\mu_1, \mu_2, ...\) of a sequence \(x_1, x_2, ...\) can be computed incrementally:
\[ \begin{align} \mu_k &= \frac{1}{k}\sum_{j=1}^{k}x_j\\ &= \frac{1}{k}\Bigl(x_k+\sum_{j=1}^{k-1}x_j \Bigr)\\ &= \frac{1}{k}(x_k + (k-1)\mu_{k-1})\\ &= \mu_{k-1} + \frac{1}{k}(x_k - \mu_{k-1}) \end{align} \]
根據上式我們可以得出增量式進行MC更新的公式:
每次 episode 結束後,增量式更新 \(V(s)\),對於每個狀態 \(S_t\),其對應的 return 為 \(G_t\)
\[ N(S_t) ← N(S_t) + 1 \\ V(S_t) ← V(S_t) + \frac{1}{N(S_t)}(G_t - V(S_t)) \]
在非靜態問題中,更新公式形式可以改為如下:
\[V(S_t) ← V(S_t) + \alpha (G_t - V(S_t))\]
時序差分學習
時序差分方法(Temporal-Difference Methods,簡稱TD)特點:
- TD 可以通過 bootstrapping 從非完整的 episodes 中學習
- TD updates a guess towards a guess
TD(λ)
下圖為 TD target 在不同 n 下的示意圖:
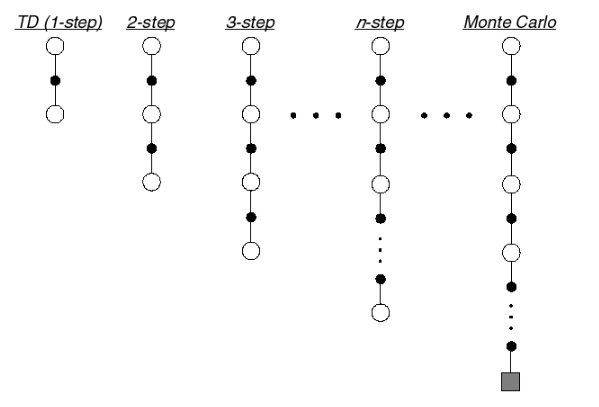
從上圖可以看出,當 n 達到終止時,即為一個episode,此時對應的方法為MC,因此從這個角度看,MC屬於TD的特殊情況。
n-step Return
n-step returns 可以表示如下:
\(n=1\) 時:\(G_{t}^{(1)} = R_{t+1} + \gamma V(S_{t+1})\)
\(n=2\) 時:\(G_{t}^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 V(S_{t+2})\)
...
\(n=\infty\) 時:\(G_{t}^{\infty} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1} R_T)\)
因此,n-step return \(G_{t}^{(n)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n}V(S_{t+n}))\)
n-step TD 更新公式:
\[V(S_t) ← V(S_t) + \alpha (G_t^{(n)} - V(S_t))\]
Forward View of TD(λ)
我們能否把所有的 n-step return 組合起來?答案肯定是可以,組合後的return被稱為是\(\lambda\)-return,其中\(\lambda\)是為了組合不同的n-step returns引入的權重因子。
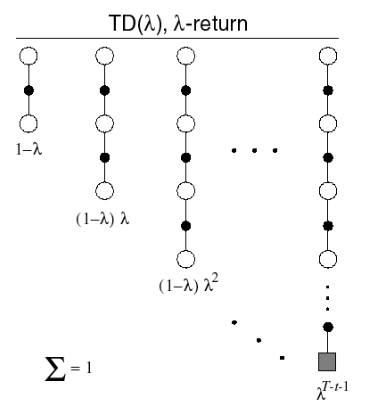
\(\lambda\)-return:
\[G_t^{\lambda} = (1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}G_t^{(n)}\]
Forward-view TD(\(\lambda\)):
\[V(S_t) ← V(S_t) + \alpha\Bigl(G_t^{\lambda} - V(S_t)\Bigr)\]
TD(\(\lambda\))對應的權重公式為 \(( 1-\lambda)\lambda^{n-1}\),分佈圖如下所示:
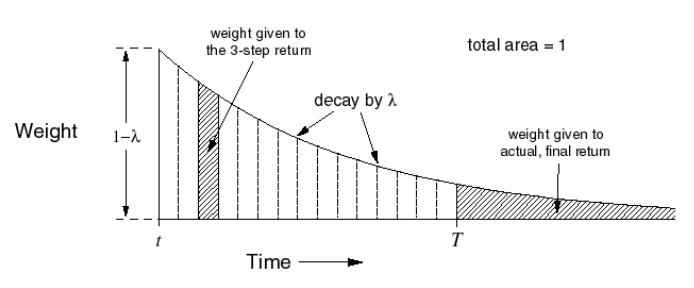
Forward-view TD(\(\lambda\))的特點:
- Update value function towards the λ-return
- Forward-view looks into the future to compute \(G_t^{\lambda}\)
- Like MC, can only be computed from complete episodes
Backward View TD(λ)
- Forward view provides theory
- Backward view provides mechanism
- Update online, every step, from incomplete sequences
帶有資格跡的TD(\(\lambda\)):
\[ \delta_t = R_{t+1} + \gamma V(S_{t+1} - V(S_t))\\ V(s) ← V(s) + \alpha \delta_t E_t(s) \]
其中\(\delta_t\)為TD-error,\(E_t(s)\)為資格跡。
資格跡(Eligibility Traces)
資格跡本質就是對於頻率高的,最近的狀態賦予更高的信任(credit)/ 權重。
下圖是對資格跡的一個描述:
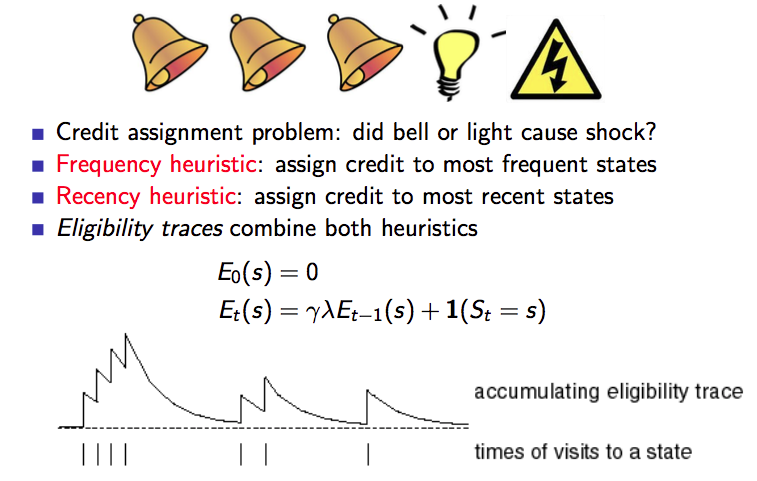
關於TD(\(\lambda\))有一個結論:
The sum of offline updates is identical for forward-view and backward-view TD(λ).
這一塊的內容不再深入介紹了,感興趣的可以看Sutton的書和David的教程。
蒙特卡洛學習 vs. 時序差分學習
MC與TD異同點
相同點:都是從經驗中線上的學習給定策略 \(\pi\) 的價值函式 \(v_{\pi}\)
不同點:
- Incremental every-visit Monte-Carlo:朝著真實的 return \(\color{Red}{G_t}\) 更新 \(V(S_t)\)
\[V(S_t) ← V(S_t) + \alpha (\color{Red}{G_t} - V(S_t))\] - Simplest temporal-difference learning algorithm: TD(0)
- 朝著已預估的 return \(\color{Red}{R_{t+1} + \gamma V(S_{t+1})}\) 更新 \(V(S_t)\)
\[V(S_t) ← V(S_t) + \alpha (\color{Red}{R_{t+1} + \gamma V(S_{t+1})} - V(S_t))\] - \(\color{Red}{R_{t+1} + \gamma V(S_{t+1})}\) 稱為是 TD target
- \(\color{Red}{R_{t+1} + \gamma V(S_{t+1})} - V(S_t)\) 稱為是 TD error
- 朝著已預估的 return \(\color{Red}{R_{t+1} + \gamma V(S_{t+1})}\) 更新 \(V(S_t)\)
下圖以 Drive Home 舉例說明兩者的不同,MC 只能在回家後才能改變對回家時間的預判,而 TD 在每一步中不斷根據實際情況來調整自己的預判。
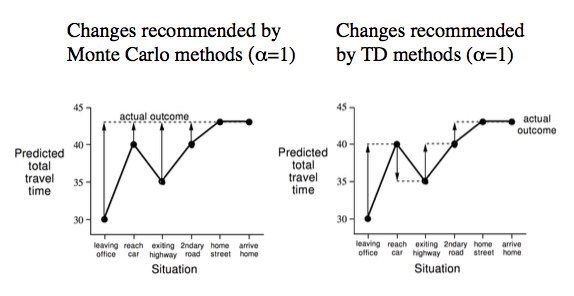
MC與TD優缺點
學習方式
- TD 可以在知道最後結果之前學習(如上圖舉例)
- TD can learn online after every step
- MC must wait until end of episode before return is known
- TD 可以在不存在最後結果的情況下學習(比如無限/連續MDPs)
- TD can learn from incomplete sequences
- MC can only learn from complete sequences
- TD works in continuing (non-terminating) environments
- MC only works for episodic (terminating) environments
方差與偏差
- MC has high variance, zero bias(高方差,零偏差)
- Good convergence properties
- Not very sensitive to initial value
- Very simple to understand and use
- TD has low variance, some bias(低方差,存在一定偏差)
- Usually more efficient than MC
- TD(0) converges to \(v_{\pi}(s)\)
- More sensitive to initial value
關於 MC 和 TD 中方差和偏差問題的解釋:
- MC 更新基於真實的 return \(G_t = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1}R_{T}\) 是 \(v_{\pi}(S_t)\) 的無偏估計。
- 真實的TD target \(R_{t+1} + \gamma v_{\pi}(S_{t+1})\) 也是 \(v_{\pi}(S_t)\) 的無偏估計。但是實際更新時用的 TD target \(R_{t+1} + \gamma V(S_{t+1})\) 是 \(v_{\pi}(S_t)\) 的有偏估計。
- TD target 具有更低的偏差:
- Return 每次模擬依賴於許多的隨機動作、轉移概率以及回報
- TD target 每次只依賴一次隨機動作、轉移概率以及回報
馬爾可夫性
- TD exploits Markov property
- Usually more efficient in Markov environments
- MC does not exploit Markov property
- Usually more effective in non-Markov environments
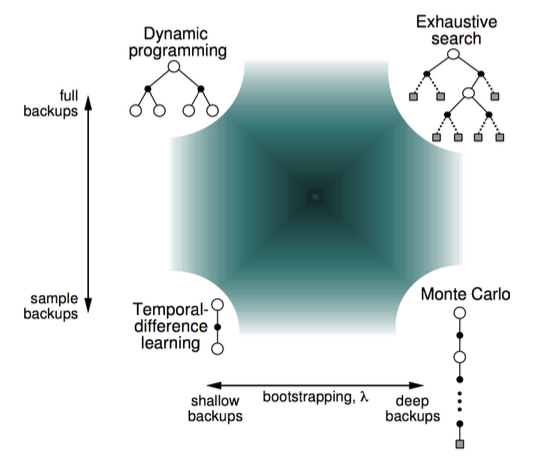
DP、MC以及TD(0)
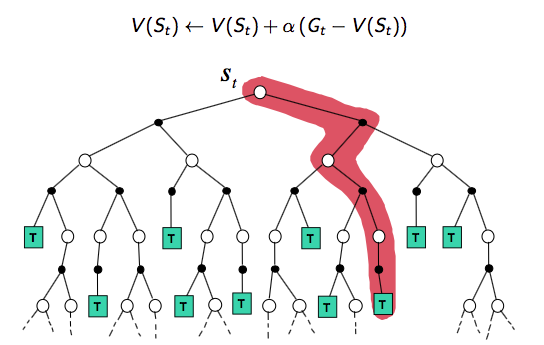
首先我們從 backup tree 上去直觀地認識三者的不同。
DP backup tree:Full-Width step(完整的step)
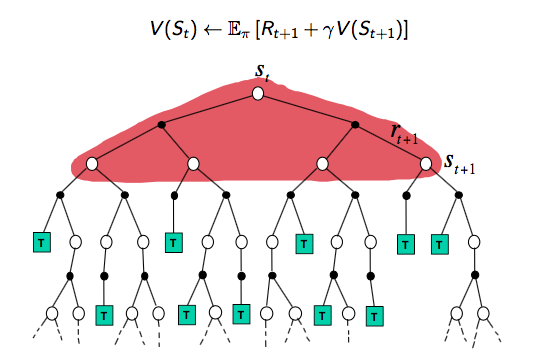
MC backup tree:完整的episode
TD(0) backup tree:單個step
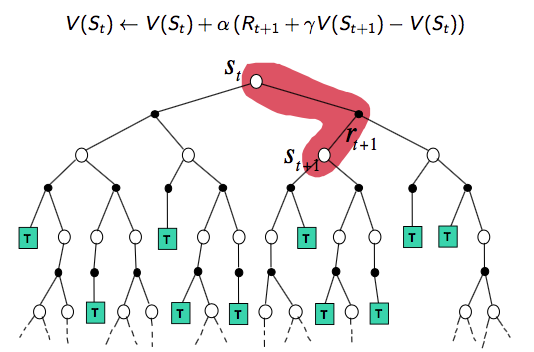
Bootstrapping vs. Sampling
Bootstrapping:基於已預測的值進行更新
- DP bootstraps
- MC does not bootstrap
- TD bootstraps
Sampling:基於取樣的期望來更新
- DP does not sample(model-based methods don't need sample)
- MC samples(model-free methods need sample)
- TD samples(model-free methods need sample)
下圖從巨集觀的視角顯示了 RL 的幾種基本方法的區別:
Reference
[1] 維基百科-蒙特卡洛方法
[2] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018
[3] David Silver's Homepage
