2.用連結串列表示多項式
最近真是被數字邏輯電路和高數折磨得夠嗆。
抽出時間
堅持更新!
今天我們談一談凡是談連結串列都一定會提到的多項式問題。
看問題!
定義多項式F(X)=∑ni=0aiXi,我們如何在計算機中儲存這個多項式?
1.用簡單陣列來儲存多項式的係數
顯然,假設這個多項式有n項,我們需要一個大小為n的陣列來儲存所有的係數,便可以通過簡單的陣列遍歷以及簡單運算來完成多項式的運算等任務。
現在思考一個問題。
編寫程式計算多項式F(X)=X+X100與G(X)=X+X101的和與積。
現在我們分析一下用陣列實現的過程,畫手登場!
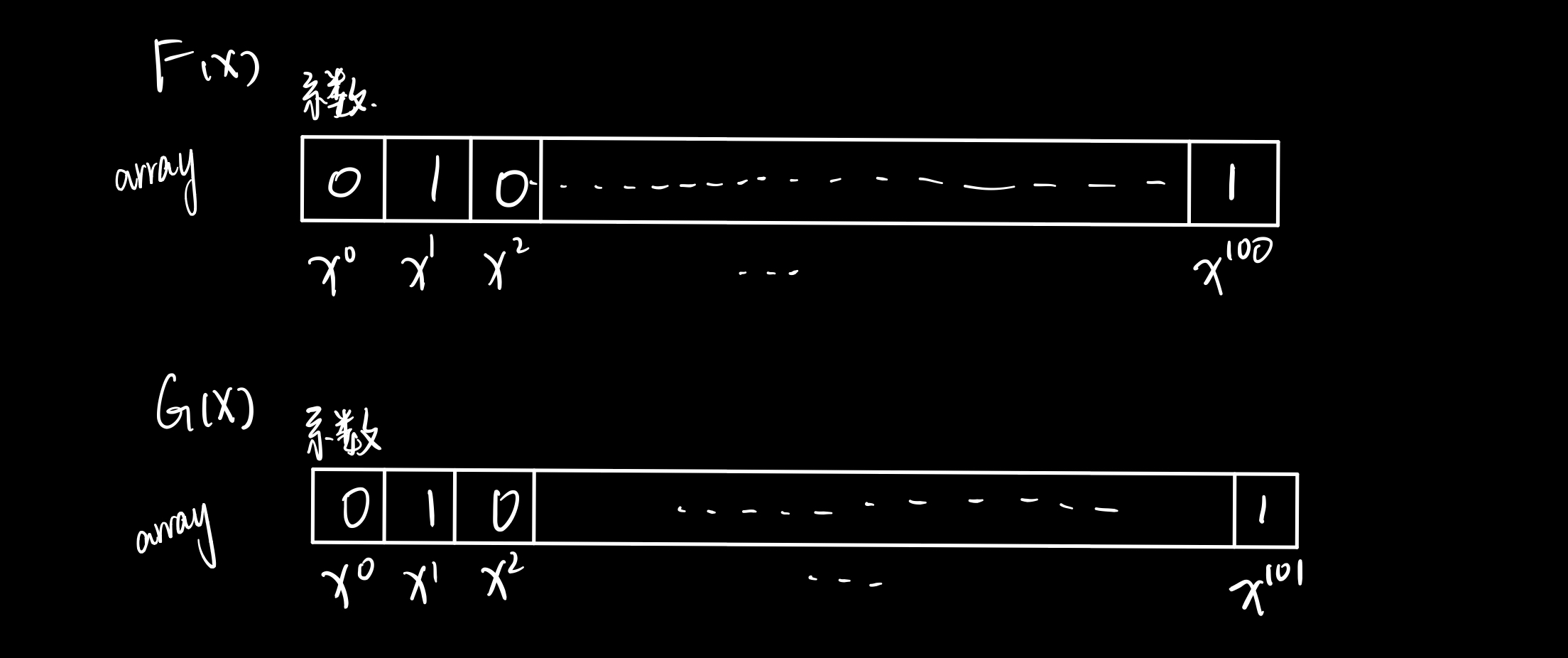
首先是和,計算過程應該是對兩個陣列進行遍歷,對每個下標相同的的元素內的值進行加法運算,如果結果不為0則輸出和以及對應X的冪
如果我們忽略進行加法運算所需的時間,將遍歷時標誌物自增所需的時間定為單位時間i,經過計算可以得出,這一個計算和的操作所需時間為201i
現在再來看乘法運算,時間需要多少?
同樣,我們忽略進行乘法運算以及合併同類項所需的時間,這個操作需要兩個for迴圈的巢狀,所需時間為100*101i,可以發現時間大量增加。
事實上,無論是加法還是乘法運算,使用陣列對多項式進行操作時,將會有大量時間耗費在對0係數項的遍歷上,尤其是當一個多項式0項很多時。
而事實上,這些0項並沒有參與計算,只是徒增了檢查0項而消耗掉的時間。
既然沒有參與計算,那能不能不儲存他們呢?
簡單陣列是無法實現的,因為其對X指數的判斷與陣列下標有關,所以無法去掉任何一項。
2.用連結串列來實現
回到剛才的題目
編寫程式計算多項式F(X)=X+X100與G(X)=X+X101的和與積。
這個計算初中生小明都會,和就是同類項合併,積就是先交叉相乘再合併同類項就可以了,他根本不會想到0項。
我們使用連結串列的話也可以做到這一點,只儲存非0項。
不過這個時候連結串列中的結點不僅僅只含一個值了,含有一個項的係數以及指數以及指向下一項的指標。
typedef struct DXHnode{ int index;//指數 float coef;//係數 struct DXHnode * next; }D_Node; typedefstruct{ D_Node *head; }Dxs;
知識基礎:結構,型別
下面是從鍵盤讀取並建立多項式連結串列的具體操作。(歡迎指正與批評)
typedef struct DXHnode{ int index;//指數 float coef;//係數 struct DXHnode * next; }D_Node; typedef struct{ D_Node *head; }Dxs; void creat_dxs(Dxs*a){ int indexx; float coeff; int n=1; printf("接下來,請根據提示輸入多項式每一項的指數和係數,當輸入的係數為0時結束判斷輸入結束\n"); while (1) { printf("請輸入第%d項的係數和指數,用空格號隔開\n",n); scanf("%f %d",&coeff,&indexx); if (coeff) { D_Node*p=(D_Node*)malloc(sizeof(D_Node)); n++; p->index=indexx; p->coef=coeff; p->next=NULL;//創造出一個結點 D_Node*last=a->head; if(last){ while(last->next) last = last->next; last->next=p; } else a->head=p; } else { printf("end of entering\n");break; } } }
現在,我們終於可以像小明一樣簡單的進行計算了!
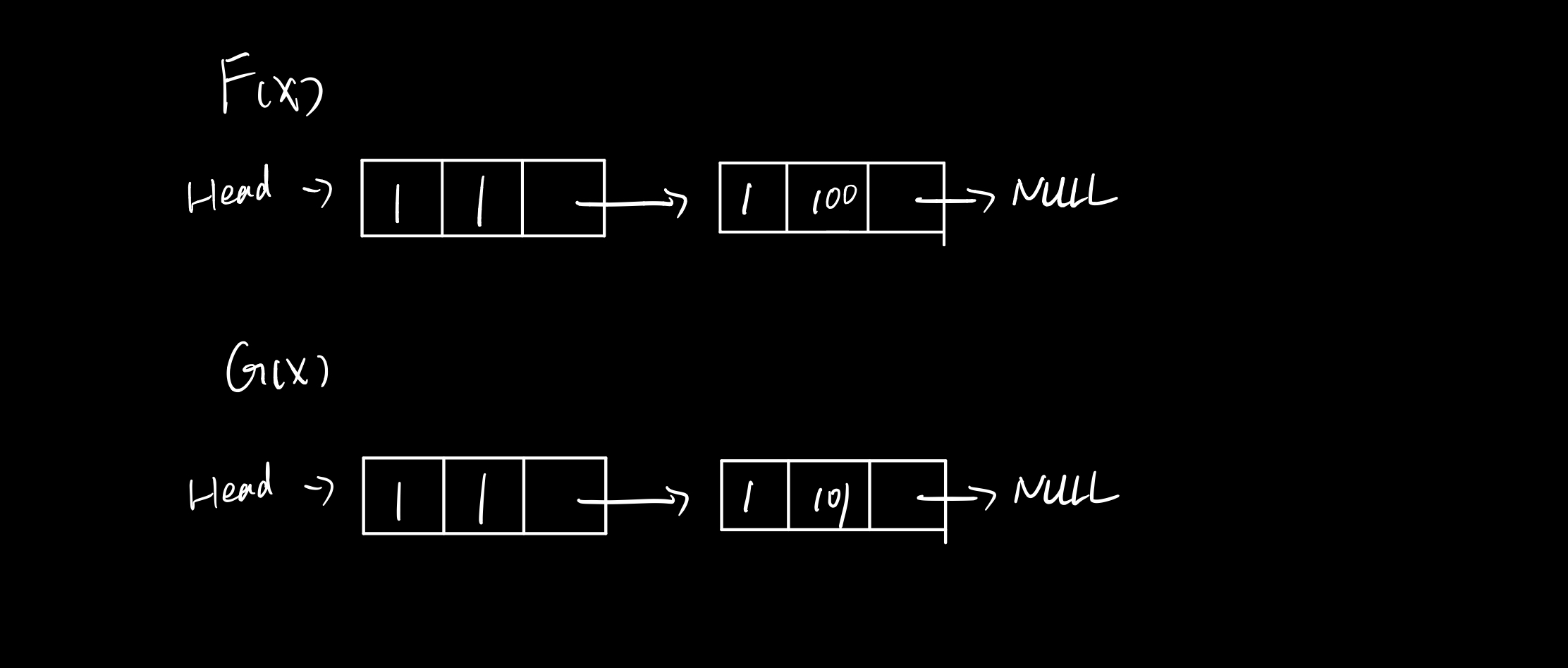
現在和與積運算需要多少時間呢?
2i(遍歷時間)
計算時間和陣列的相同。
成功避免了在0項上浪費時間。
謝謝閱讀!
