二維碼詳解(QR Code)
作者:王子旭
連結:https://zhuanlan.zhihu.com/p/21463650
來源:知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權,非商業轉載請註明出處。
2016.7.5 更新:長文多圖程式碼預警,電腦食用效果更佳。
完整版程式碼已上傳 GitHub,後續一些有的沒的的程式碼更新也都在GitHub上(https://github.com/LaytonW/qrcode)
給結尾的幾個被自動識別的QR碼做了防自動識別。。順便也檢測一下我們這不怎麼高的容錯率(7%)。要是再被知乎自動識別了。。。_(:з」∠)_
======================================================================
作為一隻程式猿,第一篇文章自然要寫hello world,但是吶,我看你們今天這樣熱情,只寫一句hello world就悶聲你們又不高興。剛好最近實習工作在處理QR碼,就來薛習一下QR碼版本的hello world吧。
-
前期準備
-
背景資訊
要想實現一個QR碼生成器,我們首先需要了解什麼是QR碼,QR碼有哪些型別,以及QR碼是如何工作的。
QR碼(Quick Response Code) 是二維碼的一種,在正方形二位矩陣內通過黑白標識編碼二進位制位從而編碼資料,最早發明用於日本汽車製造業追蹤零部件。QR碼現有40個標準版本,4個微型版本。QR碼的資料編碼方式有四種:
- 數字(Numeric):0-9
- 大寫字母和數字(alphanumeric):0-9,A-Z,空格,$,%,*,+,-,.,/,:
- 二進位制/位元組:通過 ISO/IEC 8859-1 標準編碼
- 日本漢字/假名:通過 Shift JISJIS X 0208 標準編碼
QR碼還有四種容錯級別可以選擇:
- L(Low):7%的字碼可被修正
- M(Medium):15%的字碼可被修正
- Q(Quartile):25%的字碼可被修正
- H(High):30%的字碼可被修正
(Wikipedia: QR code,
(40+4)×4×4=...... ∑(っ °Д °;)っ 咳。。好,那我們為了讀者著想 (←_←),只實現 Version 1-Byte mode-Low error control 的QR碼生成就好了嗯。。
咳。。好,那我們為了讀者著想 (←_←),只實現 Version 1-Byte mode-Low error control 的QR碼生成就好了嗯。。
好我們繼續。
如今QR碼隨處可見,大家閱碼無數可能也發現了一些規律:這些QR碼有大有小、有紅有綠,有些還有各種裝飾,但是它們總有一些部分看起來十分相似,比如三個角落裡總有“回”字形的圖樣。這就要談到QR碼的結構了。
- 結構
除了儲存編碼的資料,QR碼裡還含有一些基本標準裡欽定的圖樣來幫助掃描軟體快速識別和解碼。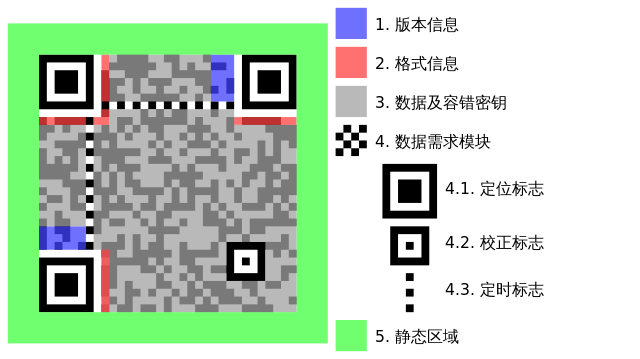 (圖片來源:Wikipedia:QR碼,https://zh.wikipedia.org/wiki/QR%E7%A2%BC)
(圖片來源:Wikipedia:QR碼,https://zh.wikipedia.org/wiki/QR%E7%A2%BC)
標準(ISO/IEC 18004)裡是這樣說的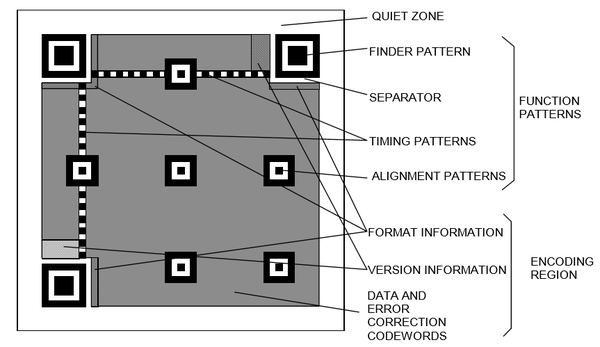 (圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
所以說我們做QR碼啊,還是要按照QR標準,按照基本標準來。我沒有任何硬點這些圖樣的意思,它們都是有自己的作用的,我們一個一個說。
-
- 功能性圖樣(function patterns):不參與編碼資料的區域。
-
-
- 悶聲區(quite zone):標準中規定標準QR碼(Ver1-40)四周應有寬4個單位、微型QR碼四周應有寬2個單位的區域顏色等效於QR碼中白色點(light module),其中不能有圖樣或標記,以保證QR碼清晰可識別。
- 定位標識(finder pattern):之前提到的“回”字形標識,位於QR碼的左上,右上和左下角,用於協助掃描軟體定位QR碼並變換座標系。定位標識可以讓QR碼在任意角度被掃描,這是一維條形碼做不到的。
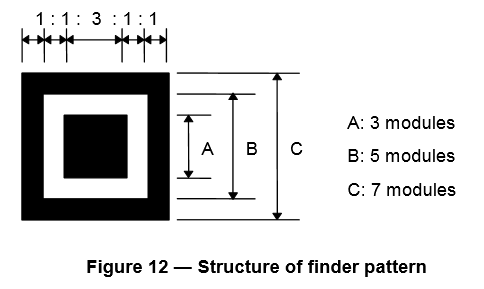 (圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification) - 分隔符(separator):一單位寬的白色點帶,位於每個定位標識和編碼區域之間用於區分。
- 定時標識(timing pattern):一單位寬的黑白交替點帶,由黑色起始和結束,用於指示標識密度和確定座標系。
- 校正標識(alignment pattern):只有 Version 2 及以上的QR碼有校正標識。校正標識用於進一步校正座標系。校正標識的數量取決於版本。
- 編碼區域(encoding region):編碼資料的區域。
- 格式資訊(format information):儲存容錯級別和資料掩碼,和額外的自身BCH容錯碼,講到再展開。
- 版本資訊(version information):儲存版本資訊。
- 資料及容錯字碼(data and error correction codewords):儲存編碼方式,實際編碼的資料和資料的RS容錯碼。
-
以上就是QR碼的通用結構標準了,再來看一看我們要實現的 Version 1 QR碼的結構: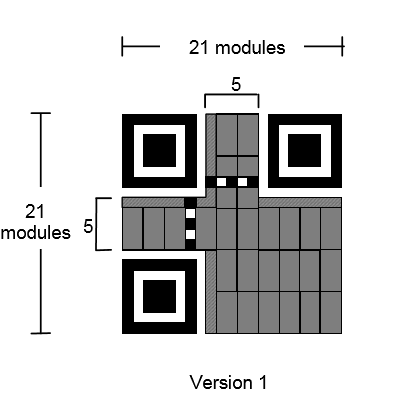
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
分析完了QR碼的結構,豁然開朗,這東西也不就這麼回事嘛,簡單!開始做!(多年以後,當程式猿面對電腦螢幕的時候,將會回想起不懂事的自己立起flag的那個下午)
- 流程
方便的是,標準也規定了將資料編碼成QR碼的流程:
- 資料分析(data analysis):分析輸入資料,根據資料決定要使用的QR碼版本、容錯級別和編碼模式。低版本的QR碼無法編碼過長的資料,含有非數字字母字元的資料要使用擴充套件字元編碼模式。因為我們只實現 V1-L byte mode QR碼,此步略去。
- 編碼資料(data encoding):根據選擇的編碼模式,將輸入的字串轉換成位元流,插入模式標識碼(mode indicator)和終止識別符號(terminator),把位元流切分成八位元的位元組,加入填充位元組來滿足標準的資料字碼數要求。
- 計算容錯碼(error correction coding):對步驟二產生的位元流計算容錯碼,附在位元流之後。高版本的編碼方式可能需要將資料流切分成塊(block)再分別進行容錯碼計算。
- 組織資料(structure final message):根據結構圖把步驟三得到的有容錯的資料流切分,準備填充。
- 填充(module placement in matrix):把資料和功能性圖樣根據標準填充到矩陣中。
- 應用資料掩碼(data masking):應用標準中的八個資料掩碼來變換編碼區域的資料,選擇最優的掩碼應用。講到再展開。
- 填充格式和版本資訊(format and version information):計算格式和版本資訊填入矩陣,完成QR碼。
簡單! ( ̄ε(# ̄)☆╰╮( ̄▽ ̄///) ↓↓↓
-
程式碼實戰
為(yin)了(wei)可(wo)讀(lan)和簡單,我們用 Python 來實現這個簡化版QR碼生成器。為了生成和操作影象,我們需要安裝第三方影象處理庫 Python Imaging Library (PIL) 。限於篇幅,本文不對PIL的使用做過多介紹,入門可參見 PIL - 廖雪峰的官方網站,Python Imaging Library Handbook。
因為程式需要處理矩陣,方便起見在這裡先定義座標系統。以矩陣的左上角為原點,原點座標定義為(0,0),i 軸向右,座標 i 對應列;j 軸向下,座標 j 對應行。於是對於影象中的畫素(i,j),有矩陣元素 mat [ j ] [ i ] 與之對應。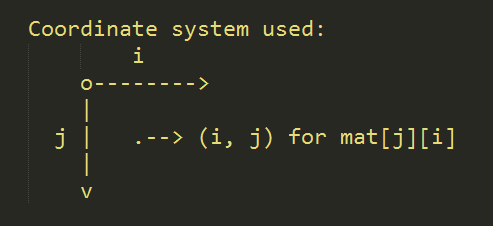
新建Python程式碼檔案 qrcode.py,引入需要的庫:
# qrcode.py
from PIL import Image, ImageDraw
為了思維簡便,我們自頂向下地構建程式碼。首先,假設我們已經填充好了一個QR碼的矩陣bitmap,我們需要把相應的影象生成出來。這裡就有了影象大小的問題:Version 1 的QR碼錶示為 21×21 的矩陣,直接把這個矩陣當做點陣圖來輸出的話,影象只有21畫素寬。為了獲得大小合適的影象,我們先定義影象大小,再把每一個畫素對映到合適的矩陣元素上。
在 qrcode.py 中新增如下程式碼:
def _genImage(bitmap, width, filename):
'''
Generate image corresponding to the input bitmap
with specified width and filename.
'''
# New image in black-white mode initialized with white.
img = Image.new('1', (width, width), 'white')
drw = ImageDraw.Draw(img)
# Normalized pixel width.
pwidth = width / len(bitmap)
for j in range(width):
# Normalized j coordinate in bitmap
normalj = j / pwidth
for i in range(width):
# Normalized i coordinate in bitmap
normali = i / pwidth
if normalj < len(bitmap) and normali < len(bitmap):
# Draw pixel.
drw.point((i, j), fill=bitmap[normalj][normali])
img.save(filename)
這個函式接收三個引數:QR碼矩陣bitmap,影象寬度width,儲存檔名filename。
img = Image.new('1', (width, width), 'white')
drw = ImageDraw.Draw(img)
這兩行初始化了影象和繪圖工具。初始化影象時的引數 '1' 代表生成黑白模式影象,'white' 代表影象初始化填充白色。
pwidth = width / len(bitmap)
用影象寬度除以矩陣維度得到標準化後的畫素寬度(QR碼中一個單位對應的畫素數)。
normalj = j / pwidth
normali = i / pwidth
遍歷影象時,將畫素座標(i,j)標準化為矩陣座標 [ i ][ j ]。檢查不越界之後,按座標繪製畫素,最後儲存影象。
儲存程式碼後,我們測試一下這個函式。在檔案目錄開啟命令列/shell,輸入python進入Python REPL。引入qrcode然後進行測試。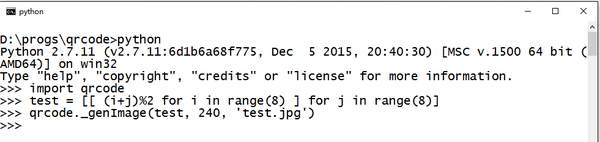
我們定義了一個矩陣 test,然後呼叫 qrcode._genImage 來生成一個240×240,名為 test.jpg 的影象如下。
我們注意到,原點處對應 (0 + 0) % 2 的畫素為黑,因為 0 值對應黑色,1 對應白色。為了明確,在 qrcode.py 中加入如下定義
_LIGHT = 1
_DARK = 0
可見我們的影象生成函式是成功的,現在只需要填充出QR碼矩陣就行了。
嗯,玩一會。。_(:з」∠)_

好我們繼續。
_genImage 函式接收QR碼矩陣作為引數,自頂向下地,我們需要生成這個矩陣。考慮到一個QR碼中有很多不變的圖樣(fixed pattern),我們可以預先填充好一個含有這些不變圖樣的模板,生成QR碼矩陣時直接把編碼好的資料填充到這個模板裡就行了。
在 qrcode.py 中加入模板的定義,待填充:
_ver1 = [[_LIGHT for i in range(21)] for j in range(21)]
假設 _ver1 是已經填充好的模板,我們生成QR碼矩陣需要怎麼做呢?根據前期準備,我們需要編碼資料,填充資料,應用掩碼,再填充格式資訊。於是我們定義這些函式:
def _fmtEncode(fmt):
'''Encode format code.'''
pass
def _encode(data):
'''
Encode the input data stream.
Add mode prefix, encode data using ISO-8859-1,
group data, add padding suffix, and call RS encoding method.
'''
pass
def _fillData(bitstream):
'''Fill the encoded data into the template QR code matrix'''
pass
def _mask(mat):
'''
Mask the data QR code matrix with all 8 masks,
and select the best mask.
'''
pass
def _fillInfo(arg):
'''
Fill the encoded format code into the masked QR code matrix.
'''
pass
def _genBitmap(bitstream):
'''
Take in the encoded data stream and generate the
final QR code bitmap.
'''
return _fillInfo(_mask(_fillData(bitstream)))
_encode 編碼資料,_fillData 將這些資料填充到模板中,_mask 應用掩碼,_fmtEncode 編碼格式資訊,_fillInfo 填充格式資訊,最後 _genBitmap 把這些函式按標準串聯起來,返回準備好的QR碼矩陣給 _genImage 來生成QR碼。
接下來我們按照流程順序實現這些函式。
- 編碼資料
首先我們要檢測輸入的資料是否超過V1-L byte mode的最大編碼長度17,如果超過就丟擲異常。在 qrcode.py 開始定義異常:
class CapacityOverflowException(Exception):
'''Exception for data larger than 17 characters in V1-L byte mode.'''
def __init__(self, arg):
self.arg = arg
def __str__(self):
return repr(self.arg)
在 _encode 中加入檢測
def _encode(data):
'''
Encode the input data stream.
Add mode prefix, encode data using ISO-8859-1,
group data, add padding suffix, and call RS encoding method.
'''
if len(data) > 17:
raise CapacityOverflowException(
'Error: Version 1 QR code encodes no more than 17 characters.')
在編碼資料之前,還要按照標準的規定加入編碼模式字首和資料字元計數,byte mode的字首是 0100,接上八位二進位制數代表的資料長度,構成資料字首。再把資料用 ISO/IEC 8859-1 標準編碼,按八個二進位制位分組,接上終止符和11101100和00010001交替的填充位元組,按標準修剪到19位元組,完成資料編碼。實現 _encode 如下:
def _encode(data):
'''
Encode the input data stream.
Add mode prefix, encode data using ISO-8859-1,
group data, add padding suffix, and call RS encoding method.
'''
if len(data) > 17:
raise CapacityOverflowException(
'Error: Version 1 QR code encodes no more than 17 characters.')
# Byte mode prefix 0100.
bitstring = '0100'
# Character count in 8 binary bits.
bitstring += '{:08b}'.format(len(data))
# Encode every character in ISO-8859-1 in 8 binary bits.
for c in data:
bitstring += '{:08b}'.format(ord(c.encode('iso-8859-1')))
# Terminator 0000.
bitstring += '0000'
res = list()
# Convert string to byte numbers.
while bitstring:
res.append(int(bitstring[:8], 2))
bitstring = bitstring[8:]
# Add padding pattern.
while len(res) < 19:
res.append(int('11101100', 2))
res.append(int('00010001', 2))
# Slice to 19 bytes for V1-L.
res = res[:19]
在L容錯等級下,編碼了資料我們還需要計算出七位的裡德-所羅門碼(可簡單了,看我和善的眼神 )
裡德-所羅門碼是 定長碼。這意味著一個固定長度輸入的資料將被處理成一個固定長度的輸出資料。在最常用的(255,223)裡所碼中,223個裡德-所羅門輸入符號(每個符號有8個 位元)被編碼成255個輸出符號。
大多數裡所錯誤校正編碼流程是成體系的。這意味著輸出的碼字中有一部分包含著輸入資料的原始形式。
符號大小為8位元的裡所碼迫使碼長( 編碼長度)最長為255個符號。
標準的(255,223)裡所碼可以在每個碼字中校正最多16個裡所符號的錯誤。由於每個符號事實上是8個位元,這意味著這個碼可以校正最多16個短爆發性錯誤。
裡德-所羅門碼,如同 卷積碼一樣,是一種透明碼。這代表如果通道符號在佇列的某些地方被反轉,解碼器一樣可以工作。解碼結果將是原始資料的補充。但是,裡所碼在縮短後會失去透明性。在縮短了的碼中,“丟失”的位元需要被0或者1替代,這由資料是否需要補足而決定。(如果符號這時候反轉,替代的0需要變成1)。於是乎,需要在裡所解碼前對資料進行強制性的偵測決定(“是”或者“補足”)。
(Wikipedia: 裡德-所羅門碼,https://zh.wikipedia.org/wiki/%E9%87%8C%E5%BE%B7-%E6%89%80%E7%BD%97%E9%97%A8%E7%A0%81)
......................................(⊙v⊙).....................................
這。。還是留給有興趣的讀者吧(微笑)
參考:Reed–Solomon codes for coders
在 _encode 之前加入如下RS容錯碼計算工具:
def _gfpMul(x, y, prim=0x11d, field_charac_full=256, carryless=True):
'''Galois field GF(2^8) multiplication.'''
r = 0
while y:
if y & 1:
r = r ^ x if carryless else r + x
y = y >> 1
x = x << 1
if prim > 0 and x & field_charac_full:
x = x ^ prim
return r
# Calculate alphas to simplify GF calculations.
_gfExp = [0] * 512
_gfLog = [0] * 256
_gfPrim = 0x11d
_x = 1
for i in range(255):
_gfExp[i] = _x
_gfLog[_x] = i
_x = _gfpMul(_x, 2)
for i in range(255, 512):
_gfExp[i] = _gfExp[i-255]
def _gfPow(x, pow):
'''GF power.'''
return _gfExp[(_gfLog[x] * pow) % 255]
def _gfMul(x, y):
'''Simplified GF multiplication.'''
if x == 0 or y == 0:
return 0
return _gfExp[_gfLog[x] + _gfLog[y]]
def _gfPolyMul(p, q):
'''GF polynomial multiplication.'''
r = [0] * (len(p) + len(q) - 1)
for j in range(len(q)):
for i in range(len(p)):
r[i+j] ^= _gfMul(p[i], q[j])
return r
def _gfPolyDiv(dividend, divisor):
'''GF polynomial division.'''
res = list(dividend)
for i in range(len(dividend) - len(divisor) + 1):
coef = res[i]
if coef != 0:
for j in range(1, len(divisor)):
if divisor[j] != 0:
res[i+j] ^= _gfMul(divisor[j], coef)
sep = -(len(divisor) - 1)
return res[:sep], res[sep:]
def _rsGenPoly(nsym):
'''Generate generator polynomial for RS algorithm.'''
g = [1]
for i in range(nsym):
g = _gfPolyMul(g, [1, _gfPow(2, i)])
return g
def _rsEncode(bitstring, nsym):
'''Encode bitstring with nsym EC bits using RS algorithm.'''
gen = _rsGenPoly(nsym)
res = [0] * (len(bitstring) + len(gen) - 1)
res[:len(bitstring)] = bitstring
for i in range(len(bitstring)):
coef = res[i]
if coef != 0:
for j in range(1, len(gen)):
res[i+j] ^= _gfMul(gen[j], coef)
res[:len(bitstring)] = bitstring
return res
(Source: Wikiversity:Reed–Solomon codes for coders)
在 _encode 結尾直接呼叫 _rsEncode 新增容錯碼,完成資料編碼部分。
def _encode(data):
'''
Encode the input data stream.
Add mode prefix, encode data using ISO-8859-1,
group data, add padding suffix, and call RS encoding method.
'''
if len(data) > 17:
raise CapacityOverflowException(
'Error: Version 1 QR code encodes no more than 17 characters.')
# Byte mode prefix 0100.
bitstring = '0100'
# Character count in 8 binary bits.
bitstring += '{:08b}'.format(len(data))
# Encode every character in ISO-8859-1 in 8 binary bits.
for c in data:
bitstring += '{:08b}'.format(ord(c.encode('iso-8859-1')))
# Terminator 0000.
bitstring += '0000'
res = list()
# Convert string to byte numbers.
while bitstring:
res.append(int(bitstring[:8], 2))
bitstring = bitstring[8:]
# Add padding pattern.
while len(res) < 19:
res.append(int('11101100', 2))
res.append(int('00010001', 2))
# Slice to 19 bytes for V1-L.
res = res[:19]
# Call _rsEncode to add 7 EC bits.
return _rsEncode(res, 7)
- 資料切分和填充
(在我完成這個專案之後,想了想資料填充有更優雅的方式,還可以通用在其他版本的QR碼上。感興趣或者是想到的讀者可以自行實現優化的 _fillData)
QR碼標準將八個二進位制位(一位元組)規定為一個數據元組,先將編碼後資料的每一個位元組填充到 2×4 的矩陣(高版本QR碼中會出現不規則形狀的位元組元組,本文中不考慮。)中,再將這些小的矩陣填入QR碼矩陣。標準也規定了位元組填入小矩陣的方式: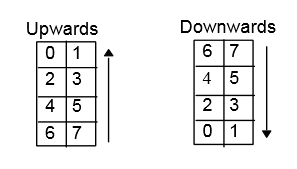
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
其中,7代表位元組最高位(most significant bit),0代表最低位(least significant bit)。
在 _fillData 前新增 _fillByte 來實現單個位元組的填充:
def _fillByte(byte, downwards=False):
'''
Fill a byte into a 2 by 4 matrix upwards,
unless specified downwards.
'''
bytestr = '{:08b}'.format(byte)
res = [[0, 0], [0, 0], [0, 0], [0, 0]]
for i in range(8):
res[i/2][i%2] = not int(bytestr[7-i])
if downwards:
res = res[::-1]
return res
有了填充好的小矩陣,接下來就把它們填入大矩陣中。標準規定的填充方式為:由大矩陣的右下開始向上填充,遇到編碼區域的邊界後向左,改為向下填充,如此蛇行將資料填入資料區域。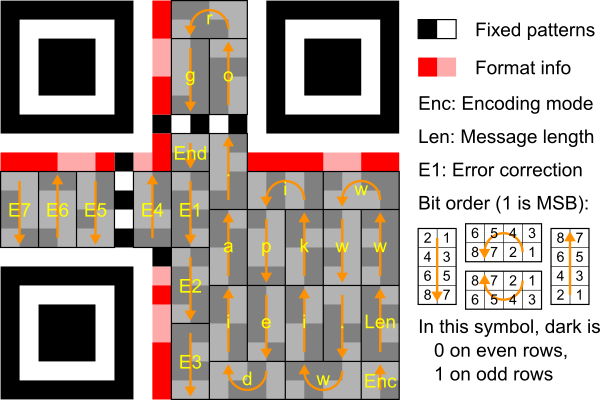
(圖片來源:Wikipedia:QR code,https://en.wikipedia.org/wiki/QR_code)
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
考慮到將小矩陣填入大矩陣的操作會非常頻繁,我們把它寫成函式來實現複用。在 qrcode.py 開始新增函式
def _matCp(src, dst, top, left):
'''
Copy the content of matrix src into matrix dst.
The top-left corner of src is positioned at (left, top)
in dst.
'''
res = copy.deepcopy(dst)
for j in range(len(src)):
for i in range(len(src[0])):
res[top+j][left+i] = src[j][i]
return res
要實現 _fillData,我們就會用到之前說的模板矩陣,那我們先把模板矩陣填充出來吧。
我們的想法是在模板矩陣中填入在所有V1-L QR碼中都固定不變的標識來簡化生成過程,那麼首先我們得找出所有這樣固定不變的標識。之前提到的功能性標識包含了大部分固定的圖樣,那麼我們先填充出這些功能性標識。定位標識和校正標識可以定義為變數,但是定時標識會隨版本變化有長度變化,為了程式碼的可擴充套件性,我們把定時標識定義為生成函式。
在 qrcode.py 開始新增定義:
def _transpose(mat):
'''Transpose a matrix'''
res = [[mat[j][i] for j in range(len(mat))] for i in range(len(mat[0]))]
return res
def _timSeq(len, vertical=False):
'''
Generate a horizontal, unless specified vertical
timing sequence with alternating dark and light
pixels with length len.
'''
res = [[i % 2 for i in range(len)]]
if vertical:
res = _transpose(res)
return res
# Finder pattern.
_finder = _matCp(_matCp([[_DARK for i in range(3)] for j in range(3)],
[[_LIGHT for i in range(5)] for j in range(5)], 1, 1),
[[_DARK for i in range(7)] for j in range(7)], 1, 1)
# Alignment pattern. Not used in version 1.
_align = _matCp(_matCp([[_DARK]],
[[_LIGHT for i in range(3)] for j in range(3)], 1, 1),
[[_DARK for i in range(5)] for j in range(5)], 1, 1)
有了這些功能性標識,先別急著往模板裡填。仔細讀標準我們會發現,在格式資訊區域也有一個固定不變的黑點。
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
實際上這張圖裡就是 Version 1 QR碼裡全部的不變樣式了。繼續在 qrcode.py 中填充模板:
# Version 1 QR code template with fixed patterns.
_ver1 = [[_LIGHT for i in range(21)] for j in range(21)]
_ver1 = _matCp(_finder, _ver1, 0, 0)
_ver1 = _matCp(_finder, _ver1, 14, 0)
_ver1 = _matCp(_finder, _ver1, 0, 14)
_ver1 = _matCp(_timSeq(5), _ver1, 6, 8)
_ver1 = _matCp(_timSeq(5, vertical=True), _ver1, 8, 6)
_ver1 = _matCp([[_DARK]], _ver1, 13, 8)
我們的模板矩陣就完成了,效果如圖:
為了避免填充過程修改模板而導致後續QR碼生成出錯,保險起見我們只通過deepcopy使用這個模板,在 qrcode.py 頭部加入模組引入:
import copy
然後實現 _fillData 如下:
def _fillData(bitstream):
'''Fill the encoded data into the template QR code matrix'''
res = copy.deepcopy(_ver1)
for i in range(15):
res = _matCp(_fillByte(bitstream[i], (i/3)%2!=0),
res,
21-4*((i%3-1)*(-1)**((i/3)%2)+2),
21-2*(i/3+1))
tmp = _fillByte(bitstream[15])
res = _matCp(tmp[2:], res, 7, 11)
res = _matCp(tmp[:2], res, 4, 11)
tmp = _fillByte(bitstream[16])
res = _matCp(tmp, res, 0, 11)
tmp = _fillByte(bitstream[17], True)
res = _matCp(tmp, res, 0, 9)
tmp = _fillByte(bitstream[18], True)
res = _matCp(tmp[:2], res, 4, 9)
res = _matCp(tmp[2:], res, 7, 9)
for i in range(3):
res = _matCp(_fillByte(bitstream[19+i], True),
res, 9+4*i, 9)
tmp = _fillByte(bitstream[22])
res = _matCp(tmp, res, 9, 7)
for i in range(3):
res = _matCp(_fillByte(bitstream[23+i], i%2==0),
res, 9, 4-2*i)
return res
這是一個非常ad hoc的實現,程式碼長但是沒有什麼技術含量。
測試一下填入資料的效果: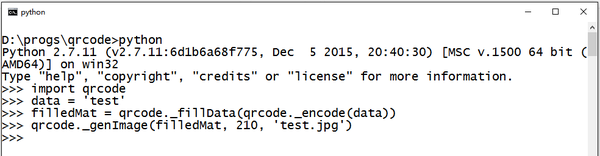

已經有一些QR碼的樣子了! <( ̄︶ ̄)> (沒有完成,這是無法掃描的)
- 掩碼和懲♂罰
得到了填入資料的矩陣,下一步就是應用掩碼來變換資料圖樣。那有人要問了,既然我們已經把資料編入了QR碼,想編碼的資訊就已經在裡面了,為什麼不直接填入格式資訊得到QR碼,而要多進行這麼一步操作呢?
掩碼真的是多此一舉嗎?你們吶還是要提高自身的姿勢水平。QR碼是要拿來掃描的,而掃描怕的就是無法清晰地分辨出編碼資訊的每一位。要是QR碼中黑白點數量不均,或是空間分佈不均都會導致大色塊區域的出現,而大色塊區域的出現會增加掃描時定位的難度,從而降低掃描的效率。更嚴重的情況下,如果資料填入後碰巧出現了功能性標識,比如定位標識的圖樣,還會干擾正常功能性標識的作用,導致QR碼無法掃描。
舉個栗子: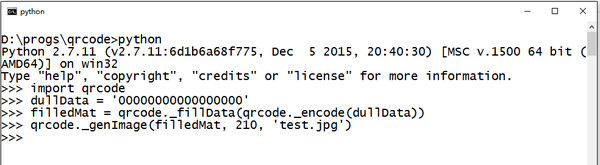

這樣的資料產生的原始QR碼明顯含有大量大面積色塊,掃描難度很高。
所以,掩碼和之前提到的在資料後新增11101100和00010001交替的填充位元組,都是為了避免這種情況發生,讓影象更“均勻”。
知道了掩碼的重要性,我們來看看掩碼到底是什麼。在電腦科學中,掩碼就是一個二進位制串,通過和資料進行異或運算來變換資料。在QR碼中,掩碼也是通過異或運算來變換資料矩陣。所以你可能已經猜到了,QR碼的掩碼就是預先定義好的矩陣。QR標準通過生成規則定義了八個資料掩碼:
- dark if (row + column) mod 2 == 0
- dark if (row) mod 2 == 0
- dark if (column) mod 3 == 0
- dark if (row + column) mod 3 == 0
- dark if ( floor(row / 2) + floor(column / 3) ) mod 2 == 0
- dark if ((row * column) mod 2) + ((row * column) mod 3) == 0
- dark if ( ((row * column) mod 2) + ((row * column) mod 3) ) mod 2 == 0
- dark if ( ((row + column) mod 2) + ((row * column) mod 3) ) mod 2 == 0
給定了規則我們很容易寫出程式碼來生成這些掩碼:

但是且慢,你看出現在出現了什麼問題嗎?
對,掩碼的範圍也覆蓋了功能性區域,要是用這樣的掩碼的話,功能性標識也難以倖免。所以我們需要一個代表資料區域的“蒙版”來過濾掉功能性區域中的掩圖案。這個“過濾”的過程可以通過矩陣間“與”運算來實現。
在 qrcode.py 開始新增矩陣間“與”運算函式和資料區域蒙版的填充:
def _matAnd(mat1, mat2):
'''
Matrix-wise and.
Dark and dark -> dark
Light and light -> light
Dark and light -> light
Light and dark -> light
'''
res = [[_LIGHT for i in range(len(mat1[0]))] for j in range(len(mat1))]
for j in range(len(mat1)):
for i in range(len(mat1[0])):
res[j][i] = int(mat1[j][i] == _LIGHT or mat2[j][i] == _LIGHT)
return res
# Data area mask to avoid applying masks to functional area.
_dataAreaMask = [[_DARK for i in range(21)] for j in range(21)]
_dataAreaMask = _matCp([[_LIGHT for i in range(9)] for j in range(9)],
_dataAreaMask, 0, 0)
_dataAreaMask = _matCp([[_LIGHT for i in range(9)] for j in range(8)],
_dataAreaMask, 13, 0)
_dataAreaMask = _matCp([[_LIGHT for i in range(8)] for j in range(9)],
_dataAreaMask, 0, 13)
_dataAreaMask = _matCp([[_LIGHT for i in range(4)]], _dataAreaMask, 6, 9)
_dataAreaMask = _matCp([[_LIGHT] for i in range(4)], _dataAreaMask, 9, 6)
填充出的資料區域蒙版效果如圖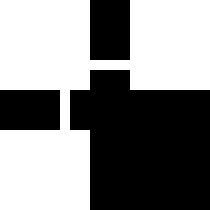
我們在定義掩碼時和蒙版進行“與”運算,就可以得到範圍正確的掩碼了。繼續新增掩碼定義
# Data masks defined in QR standard.
_dataMasks = []
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if (i+j)%2==0 else _LIGHT for i in range(21)] for j in range(21)]))
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if j%2==0 else _LIGHT for i in range(21)] for j in range(21)]))
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if i%3==0 else _LIGHT for i in range(21)] for j in range(21)]))
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if (i+j)%3==0 else _LIGHT for i in range(21)] for j in range(21)]))
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if (j/2 + i/3)%2==0 else _LIGHT for i in range(21)] for j in range(21)]))
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if (i*j)%2+(i*j)%3==0 else _LIGHT for i in range(21)] for j in range(21)]))
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if ((i*j)%2+(i*j)%3)%2==0 else _LIGHT for i in range(21)] for j in range(21)]))
_dataMasks.append(_matAnd(_dataAreaMask,
[[_DARK if ((i+j)%2+(i*j)%3)%2==0 else _LIGHT for i in range(21)] for j in range(21)]))
效果如圖
現在我們就可以安心地使用這些掩碼啦!
在 qrcode.py 開始新增矩陣間異或函式
def _matXor(mat1, mat2):
'''
Matrix-wise xor.
Dark xor dark -> light
Light xor light -> light
Dark xor light -> dark
Light xor dark -> dark
'''
res = [[_LIGHT for i in range(len(mat1[0]))] for j in range(len(mat1))]
for j in range(len(mat1)):
for i in range(len(mat1[0])):
res[j][i] = int(mat1[j][i] == mat2[j][i])
return res
因為我們用1來表示白色,0來表示黑色,所以異或和與的邏輯都是和正常邏輯相反的。
該實現 _mask 來給填了資料的QR碼應用掩碼了。可是不對啊,為什麼要八個掩碼啊?這是因為考慮到資料的多樣性,一種掩碼難以達到預期的效果,所以QR標準定義了八個掩碼,要求在應用掩碼時先分別應用所有的掩碼產生八個結果,然後根據懲罰規則計算出每個結果矩陣的懲罰分,再選出懲罰分最小,效果最好的掩碼當做最終結果。這一過程產生的掩碼ID也是格式資訊的一部分,來告訴掃描軟體應該用哪個掩碼來還原資料。
QR標準把懲罰分分成了四項,分別對應行/列中的連續色條、大面積的色塊、行/列中類似定位標識的部分、整個矩陣中顏色的不平衡做出加權懲罰。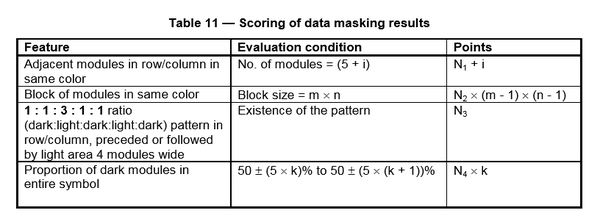
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
其中,N1=3,N2=3,N3=40,N4=10,i 是色條超出5的部分的長度。
在 _mask 之前新增 _penalty 的實現:
def _penalty(mat):
'''
Calculate penalty score for a masked matrix.
N1: penalty for more than 5 consecutive pixels in row/column,
3 points for each occurrence of such pattern,
and extra 1 point for each pixel exceeding 5
consecutive pixels.
N2: penalty for blocks of pixels larger than 2x2.
3*(m-1)*(n-1) points for each block of mxn
(larger than 2x2).
N3: penalty for patterns similar to the finder pattern.
40 points for each occurrence of 1:1:3:1:1 ratio
(dark:light:dark:light:dark) pattern in row/column,
preceded of followed by 4 consecutive light pixels.
N4: penalty for unbalanced dark/light ratio.
10*k points where k is the rating of the deviation of
the proportion of dark pixels from 50% in steps of 5%.
'''
# Initialize.
n1 = n2 = n3 = n4 = 0
# Calculate N1.
for j in range(len(mat)):
count = 1
adj = False
for i in range(1, len(mat)):
if mat[j][i] == mat[j][i-1]:
count += 1
else:
count = 1
adj = False
if count >= 5:
if not adj:
adj = True
n1 += 3
else:
n1 += 1
for i in range(len(mat)):
count = 1
adj = False
for j in range(1, len(mat)):
if mat[j][i] == mat[j-1][i]:
count += 1
else:
count = 1
adj = False
if count >= 5:
if not adj:
adj = True
n1 += 3
else:
n1 += 1
# Calculate N2.
m = n = 1
for j in range(1, len(mat)):
for i in range(1, len(mat)):
if mat[j][i] == mat[j-1][i] and mat[j][i] == mat[j][i-1] and mat[j][i] == mat[j-1][i-1]:
if mat[j][i] == mat[j-1][i]:
m += 1
if mat[j][i] == mat[j][i-1]:
n += 1
else:
n2 += 3 * (m-1) * (n-1)
m = n = 1
# Calculate N3.
count = 0
for row in mat:
rowstr = ''.join(str(e) for e in row)
occurrences = []
begin = 0
while rowstr.find('0100010', begin) != -1:
begin = rowstr.find('0100010', begin) + 7
occurrences.append(begin)
for begin in occurrences:
if rowstr.count('00000100010', begin-4) != 0 or rowstr.count('01000100000', begin) != 0:
count += 1
transposedMat = _transpose(mat)
for row in transposedMat:
rowstr = ''.join(str(e) for e in row)
occurrences = []
begin = 0
while rowstr.find('0100010', begin) != -1:
begin = rowstr.find('0100010', begin) + 7
occurrences.append(begin)
for begin in occurrences:
if rowstr.count('00000100010', begin-4) != 0 or rowstr.count('01000100000', begin) != 0:
count += 1
n3 += 40 * count
# Calculate N4.
dark = sum(row.count(_DARK) for row in mat)
percent = int((float(dark) / float(len(mat)**2)) * 100)
pre = percent - percent % 5
nex = percent + 5 - percent % 5
n4 = min(abs(pre-50)/5, abs(nex-50)/5) * 10
return n1 + n2 + n3 + n4
(插一句,我實現的這個 _penalty 還沒有測試正確性。。)
(大概仔細看完了辣麼一大段程式碼然後看到上一句的人會想來打我吧。。)
實現 _mask :
def _mask(mat):
'''
Mask the data QR code matrix with all 8 masks,
call _penalty to calculate penalty scores for each
and select the best mask.
Return tuple(selected masked matrix, number of selected mask).
'''
maskeds = [_matXor(mat, dataMask) for dataMask in _dataMasks]
penalty = [0] * 8
for i, masked in enumerate(maskeds):
penalty[i] = _penalty(masked)
# Find the id of the best mask.
index = penalty.index(min(penalty))
return maskeds[index], index
這裡考慮到 _mask 是由 _fillInfo 呼叫,而填寫格式資訊需要選擇的掩碼的ID,我們讓 _mask 返回了結果矩陣和掩碼ID構成的tuple。
用我們之前的栗子測試一下掩碼效果: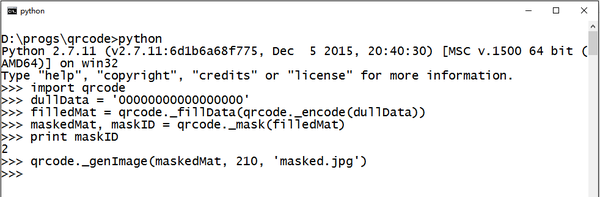

效果不錯!
- 填充格式資訊
只剩最後一步了!格式資訊很簡單,由兩位容錯等級程式碼和三位QR掩碼程式碼構成。
容錯等級程式碼: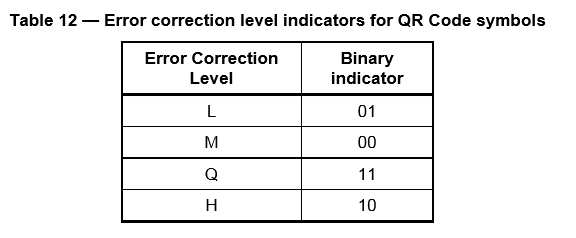
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
QR掩碼程式碼:
當然格式資訊也是要加容錯碼的。格式資訊的容錯演算法採用(15,5)BCH碼。
編碼構建碼字為
(c14, c13, ..., c8)
這樣多項式為
c14+c13+...+c8
我們將它稱為 CI。
然後就要找出 CR 滿足 CR=CI (mod m1,3(x))=c7+c6+...+c0
這樣就得到待發的碼字 C(x) = CI+CR (mod m1,3(x)) = 0
例如,如果我們要對 (1,1,0,0,1,1,0) 進行編碼
CI=x14+x13+x10+x9
然後用 m1,3(x) 除以(這裡的除法是多項式除法)CI ,得到結果為 CR(x),在Z2域中,我們可以算出 CR為
x3+1
這樣,待發的碼字為
(1,1,0,0,1,1,0, 0,0,0,0,1,0,0,1)
(Wikipedia: BCH碼,https://zh.wikipedia.org/wiki/BCH%E7%A0%81)
.......................................................
咳咳。。去看Reed–Solomon codes for coders,都講得很清楚嘛,很容易就看懂了對不對?(和善的微笑)
計算得出十位BCH容錯碼接在格式資訊之後,還要與掩碼101010000010010進行異或,作用同QR掩碼。
在 _fillInfo 之前新增 _fmtEncode 實現容錯碼計算和應用掩碼:
def _fmtEncode(fmt):
'''Encode the 15-bit format code using BCH code.'''
g = 0x537
code = fmt << 10
for i in range(4,-1,-1):
if code & (1 << (i+10)):
code ^= g << i
return ((fmt << 10) ^ code) ^ 0b101010000010010
(Source: Wikiversity: Reed–Solomon codes for coders)
有了編碼好的格式資訊,就可以把它按照標準填入矩陣了。
(圖片來源:ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification)
其中14代表最高位(most significant bit),0代表最低位(least significant bit)。
繼續實現 _fillInfo:
def _fillInfo(arg):
'''
Fill the encoded format code into the masked QR code matrix.
arg: (masked QR code matrix, mask number).
'''
mat, mask = arg
# 01 is the format code for L error control level,
# concatenated with mask id and passed into _fmtEncode
# to get the 15 bits format code with EC bits.
fmt = _fmtEncode(int('01'+'{:03b}'.format(mask), 2))
fmtarr = [[not int(c)] for c in '{:015b}'.format(fmt)]
mat = _matCp(_transpose(fmtarr[7:]), mat, 8, 13)
mat = _matCp(fmtarr[9:][::-1], mat, 0, 8)
mat = _matCp(fmtarr[7:9][::-1], mat, 7, 8)
mat = _matCp(fmtarr[:7][::-1], mat, 14, 8)
mat = _matCp(_transpose(fmtarr[:6]), mat, 8, 0)
mat = _matCp([fmtarr[6]], mat, 8, 7)
return mat
至此QR碼全部完成(撒花花 ︿( ̄︶ ̄)︿)。
- 介面
最後一步,為我們的QR碼生成器提供呼叫介面:
def qrcode(data, width=210, filename='qrcode.jpg'):
'''Module public interface'''
try:
_genImage(_genBitmap(_encode(data)), width, filename)
except Exception, e:
print e
raise e
噠噠噠噠!完成!(完整版程式碼已上傳 GitHub: https://github.com/LaytonW/qrcode)
別忘了我們最初的目的:hello world!來試驗一下吧!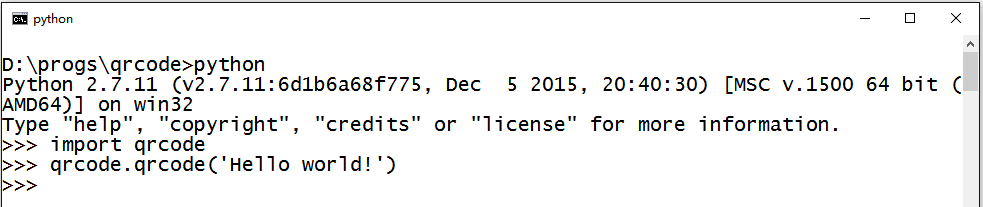
Hello world! (二維碼自動識別)
能!掃!描!了!
滿滿的成就感有沒有!!!
可是突然想到!!!
我只是想說一句 hello world啊!!!!!
那何不多說幾句啊!!


-
寫在後面
凌晨2點14,終於完稿。我只有幾點想說的
-
- 學習真有趣
- Python真好用
- 制定標準真是凝結了工程師的無限智慧
- 熬夜傷身
- 熬夜會餓
- 半夜餓真難受
- 第一次寫東西,囉囉嗦嗦拖了這麼長的篇幅
- 看到這裡的都是真愛

(END)
Reference:
Wikipedia: QR code, https://en.wikipedia.org/wiki/QR_code
Wikipedia: QR碼, https://zh.wikipedia.org/wiki/QR%E7%A2%BC
Wikipedia: Reed–Solomon error correction, https://en.wikipedia.org/wiki/Reed%E2%80%93Solomon_error_correction
Wikipedia: 裡德-所羅門碼, https://zh.wikipedia.org/wiki/%E9%87%8C%E5%BE%B7-%E6%89%80%E7%BD%97%E9%97%A8%E7%A0%81
Wikipedia: BCH code, https://en.wikipedia.org/wiki/BCH_code
Wikipedia: BCH碼, https://zh.wikipedia.org/wiki/BCH%E7%A0%81
Wikiversity: Reed–Solomon codes for coders, https://en.wikiversity.org/wiki/Reed%E2%80%93Solomon_codes_for_coders#BCH_codes
Thonky: QR Code Tutorial, http://www.thonky.com/qr-code-tutorial/
Python Imaging Library Handbook, http://effbot.org/imagingbook/pil-index.htm
ISO/IEC 18004: Information – Automatic identification and data capture techniques – QR Code barcode symbology specification
