/*
根右左遍歷後最長上升子序列
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>

using namespace std;

typedef long long LL;

inline LL read()
{
    char c=getchar();LL num=0,f=1;
    for(;!isdigit(c);c=getchar())
        f
 
=c=='-'?-1:f;
    for(;isdigit(c);c=getchar())
        num=num*10+c-'0';
    return num*f;
}

const int N=1e5+5;

int n;
LL w[N];
int son[N][2];

LL dfn[N],tim;
void dfs(int u)
{
    dfn[++tim]=w[u];
    if(son[u][1]!=0)
        dfs(son[u][1]);
    if(son[u][0]!=0)
        dfs(son[u][0]);
}

LL lis[N],len;
 
int main()
{
    freopen("point.in","r",stdin);
    freopen("point.out","w",stdout);
     int size = 256 << 20; // 256MB  
        char *p = (char*)malloc(size) + size;  
        __asm__("movl %0, %%esp\n" :: "r"(p));
 
    n=read();
    for(int i=1;i<=n;++i)
        w[i]=read();
    
 
for(int i=1;i<=n;++i)
        son[i][0]=read(),son[i][1]=read();
    dfs(1);
    lis[len=1]=dfn[1];
    for(int i=2;i<=tim;++i)
    {
        if(dfn[i]>lis[len]) lis[++len]=dfn[i];
        else lis[lower_bound(lis+1,lis+len+1,dfn[i])-lis]=dfn[i];
    }
    cout<<len;
    fclose(stdin);fclose(stdout);
    return 0;
}

/*
序列分為移動的序列和未移動的序列兩部分
詢問離散化後 
對於移動的序列，抽出來樹狀陣列統計逆序對
對於未移動的序列，想辦法能直接統計答案
首先維護哪些數未被移動過，然後對於未被移動過的數求字首和sum[i] 
這樣就得到了1~i中未被移動過的數的個數，進而能O(1)得出每段區間未被移動的數的個數。
考慮一個移動了的元素，從i向前移動到了j，那麼他對答案的貢獻，就是sum[j,i]
因為向前移動後[j,i]這段區間所有數都比他小。
同理一個元素從i向後移動到了j，那麼他對答案的貢獻為sum[i,j]
所以未被移動的元素對答案的貢獻和就是Σabs(sum[原來位置]-sum[移動後的位置]) 
*/
#include<bits/stdc++.h>

#define N 200007
#define ll long long

using namespace std;
int n,m,cnt,num;
ll ans;
ll pos[N],a[N],sum[N];
struct node{
    int L,R;
}ask[N];

struct BIT_{
    
    int n;ll a[N];
    
    static int lowbit(int x){
        
        return x & -x;
    }
    
    void clear(){
        
        for(int i=1;i<=n;i++) a[i]=0;
    }
    
    ll query(int pos){
        
        ll ans=0;
        for(int i=pos;i>0;i-=lowbit(i)) ans+=a[i];
        return ans;
    }
    
    void update(int pos,int val){
        
        for(int i=pos;i<=n;i+=lowbit(i)) a[i]+=val;
    }
}bit;

inline int read()
{
    int x=0,f=1;char c=getchar();
    while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
    return x*f;
}

void discrete()
{
    for(int i=1;i<=n;i++)
    {
        ask[i].L=read();ask[i].R=read();
        a[i]=ask[i].L;a[i+n]=ask[i].R;
        pos[i]=i;pos[i+n]=i+n;
    }
    sort(a+1,a+n*2+1);
    num=unique(a+1,a+n*2+1)-a-1;
    for(int i=1;i<=num;i++) sum[i]=sum[i-1]+a[i]-a[i-1]-1;
    for(int i=1;i<=n;i++)
    {
        ask[i].L=lower_bound(a+1,a+num+1,ask[i].L)-a;
        ask[i].R=lower_bound(a+1,a+num+1,ask[i].R)-a;
        swap(pos[ask[i].L],pos[ask[i].R]);
    }
}

int main()
{
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    n=read();discrete();
    bit.n=n<<1; bit.clear();
    for(int i=num;i>=1;i--)
    {
        ans+=bit.query(pos[i]);
        ans+=abs(sum[pos[i]]-sum[i]);
        bit.update(pos[i],1);
    }
    cout<<ans<<endl;
    return 0;
}

/*
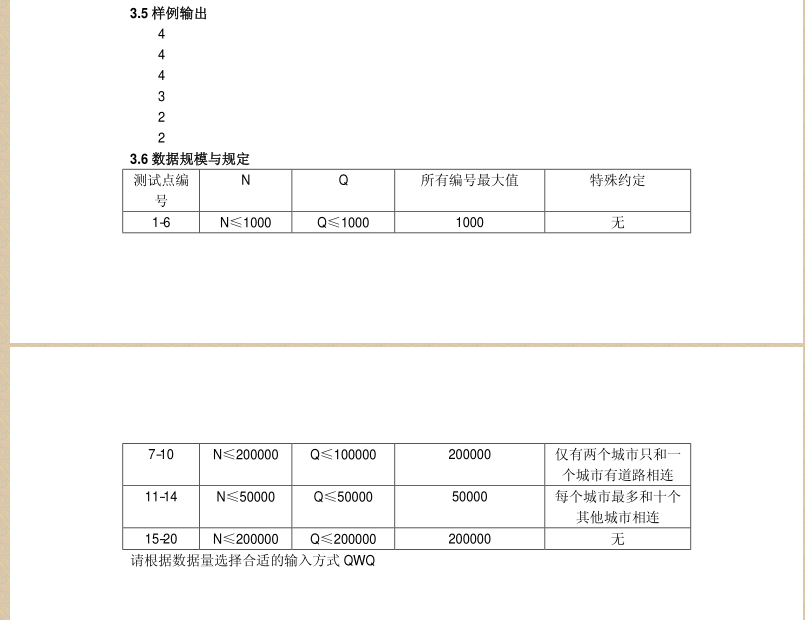
bzoj1483 放到樹上
見https://www.cnblogs.com/L-Memory/p/9898249.html 
同理 vector+啟發式合併。 
*/
#include<bits/stdc++.h>

#define ll long long
#define M 200010
using namespace std;
int read()
{
    int nm = 0, f = 1;
    char c = getchar();
    for(; !isdigit(c); c = getchar()) if(c == '-') f = -1;
    for(; isdigit(c); c = getchar()) nm = nm * 10 + c - '0';
    return nm * f;
}

int note[M], sz[M], cor[M], id[M];
vector<int>to[M], to1[M];
int n, q, ans;
void dfs(int now, int fa)
{
    if(cor[now] != 0 && cor[now] != cor[fa]) ans++;
    for(int i = 0; i < to[now].size(); i++)
    {
        int vj = to[now][i];
        if(vj == fa) continue;
        dfs(vj, now);
    }
}

void del(int x)
{
    for(int i = 0; i < to[x].size(); i++)
    {
        int vj = to[x][i];
        if(cor[vj] != cor[x]) ans--;
    }
}
void insert(int x)
{
    for(int i = 0; i < to[x].size(); i++)
    {
        int vj = to[x][i];
        if(cor[vj] != cor[x]) ans++;
    }
}
int tot = 0, tot2 = 0;
int main()
{
    freopen("simulator.in", "r", stdin);
    freopen("simulator.out", "w", stdout);
    n = read(), q = read();
    for(int i = 1; i <= n; i++) cor[i] = read(), sz[cor[i]]++, to1[cor[i]].push_back(i), id[i] = i, note[i] = i;
    for(int i = 1; i < n; i++)
    {
        int vi = read(), vj = read();
        to[vi].push_back(vj), to[vj].push_back(vi);
    }
    to[1].push_back(0), cor[0] = 0x3e3e3e3e;
    dfs(1, 0);
    while(q--)
    {
        int x = read(), y = read();
        int xn = id[x], yn = id[y];
        if(sz[xn] < sz[yn])
        {
            tot += sz[xn], tot2 += to1[xn].size();
            for(int i = 0; i < to1[xn].size(); i++)
            {
                int op = to1[xn][i];
                del(op);
                to1[yn].push_back(op);
            }
            for(int i = 0; i < to1[xn].size(); i++)
            {
                int op = to1[xn][i];
                cor[op] = yn;
            }
            for(int i = 0; i < to1[xn].size(); i++)
            {
                int op = to1[xn][i];
                insert(op);
            }
            to1[xn].clear();
            sz[yn] += sz[xn];
            sz[xn] = 0;
            id[x] = 0;
        }
        else
        {
            tot+=sz[yn], tot2 += to1[yn].size();
            for(int i = 0; i < to1[yn].size(); i++)
            {
                int op = to1[yn][i];
                del(op);
                to1[xn].push_back(op);
            }
            for(int i = 0; i < to1[yn].size(); i++)
            {
                int op = to1[yn][i];
                cor[op] = xn;
            }
            for(int i = 0; i < to1[yn].size(); i++)
            {
                int op = to1[yn][i];
                insert(op);
            }
            to1[yn].clear();
            sz[xn] += sz[yn];
            sz[yn] = 0;
            id[y] = xn;
            id[x] = 0;
        }
        cout << ans << "\n";
    }
    return 0;
}