R中因子水平的自動組合
每次我們在應用計量經濟學課程中面對實際應用時,我們都必須處理分類變數。同樣的問題也發生在學生身上:我們怎樣才能自動地結合因素水平呢?有簡單的R函式嗎?
在過去的幾年裡,我確實上傳了一些部落格文章。但到目前為止沒有什麼令人滿意的。讓我寫下幾行關於可以做什麼的話。如果有人想寫一個很好的R函式,那就太棒了。為了說明這一想法,請考慮以下(模擬資料集):
n=200
set.seed(1)
x1=runif(n)
x2=runif(n)
y=1+2*x1-x2+rnorm(n,0,.2)
LB=sample(LETTERS[1:10])
b=data.frame(y=y,x1=x1,
x2=cut(x2,breaks=
c(-1,.05,.1,.2,.35,.4,.55,.65,.8,.9,2),
labels=LB))
str(b)
'data.frame':200 obs. of 3 variables:
$ y : num 1.345 1.863 1.946 2.481 0.765 ...
$ x1: num 0.266 0.372 0.573 0.908 0.202 ...
$ x2: Factor w/ 10 levels "I","A","H","F",..: 4 4 6 4 3 6 7 3 4 8 ...
table(b$x2)[LETTERS[1:10]]
A B C D E F G H I J
11 12 23 34 23 36 12 32 3 14
有一個(連續)因變數y,一個連續協變數x_1和一個範疇變數x_2,具有十個水平。我們可以使用以下方法繪製資料:
plot(b$x1,y,col="white",xlim=c(0,1.1))
text(b$x1,y,as.character(b$x2),cex=.5)
 線性迴歸的輸出產生以下預測:
線性迴歸的輸出產生以下預測:

for(i in 1:10){
p=function(x) predict(lm(y~x1+x2,data=b),newdata=data.frame(x1=x,x2=LETTERS[i]))
u=seq(-1,1.065,by=.01)
v=Vectorize(p)(u)
lines(u,v)}
x_1的斜率是相同的,我們只需為每個級別新增一個不同的常數。正如我們所看到的,一些級別非常接近,因此將它們合併成一個類別似乎是合理的。以下是線性迴歸的輸出:
summary(lm(y~x1+x2,data=b))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.843802 0.119655 7.052 3.23e-11 ***
x1 1.992878 0.053838 37.016 < 2e-16 ***
x2A 0.055500 0.131173 0.423 0.6727
x2H 0.009293 0.121626 0.076 0.9392
x2F -0.177002 0.121020 -1.463 0.1452
x2B -0.218152 0.130192 -1.676 0.0955 .
x2D -0.206970 0.121294 -1.706 0.0896 .
x2G -0.407417 0.129999 -3.134 0.0020 **
x2C -0.526708 0.123690 -4.258 3.24e-05 ***
x2J -0.664281 0.128126 -5.185 5.54e-07 ***
x2E -0.816454 0.123625 -6.604 3.94e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2014 on 189 degrees of freedom
Multiple R-squared: 0.8995,Adjusted R-squared: 0.8942
F-statistic: 169.1 on 10 and 189 DF, p-value: < 2.2e-16
AIC(lm(y~x1+x2,data=b))
[1] -60.74443
BIC(lm(y~x1+x2,data=b))
[1] -21.16463
在這裡,參考類別是“I”。看起來我們可以把這個類別和其他幾個類別結合起來。這裡的一種策略是選擇似乎沒有明顯區別的所有類別,並執行一個(多個)測試:
library(car)
linearHypothesis(lm(y~x1+x2,data=b), c("x2A = 0", "x2H = 0", "x2F = 0"))
Hypothesis:
x2A = 0
x2H = 0
x2F = 0
Model 1: restricted model
Model 2: y ~ x1 + x2
Res.Df RSS Df Sum of Sq F Pr(>F)
1 192 8.4651
2 189 7.6654 3 0.79971 6.5726 3e-04 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
看來我們可以把這四個類別結合起來。
在這裡,我們可以看到當我們更改引用類別時發生了什麼(實際上,在所有類別上迴圈):
P=matrix(NA,nlevels(b$x2),nlevels(b$x2))
colnames(P)=rownames(P)=LETTERS[1:10]
plot(1:nlevels(b$x2),1:nlevels(b$x2),col="white",xlab="",ylab="",axes=F,xlim=c(0,10.5),
ylim=c(0,10.5))
text(1:10,0,LETTERS[1:10])
text(0,1:10,LETTERS[1:10])
for(i in 1:nlevels(b$x2)){
#levels(b$x2)=LETTERS[1:10]
b$x2=relevel(b$x2,LETTERS[i])
p=summary(lm(y~x1+x2,data=b))$coefficients[-(1:2),4]
names(p)=substr(names(p),3,3)
P[LETTERS[i],names(p)]=p
p=P[LETTERS[i],]
idx=which(p>.05)
points(((1:10))[idx],rep(i,length(idx)),pch=1,cex=2)
idx=which(p>.1)
points(((1:10))[idx],rep(i,length(idx)),pch=19,cex=2)}

我們很高興看到它是對稱的:如果“H”應該與“i”結合,那麼“i”也應該與“H”結合。
在這裡,黑點與10%p值有關,白色點與5%p值有關.這張圖其實很難讀.。事實上,這讓我們想起Bertin(1967年).

在這裡,我們可以手動預定義一些排序(下面我們將看到它是如何自動化的):
LETTERSord=c("I","A","H","F","B","D","G","C","J","E")
P=matrix(NA,nlevels(b$x2),nlevels(b$x2))
colnames(P)=rownames(P)=LETTERSord
plot(1:nlevels(b$x2),1:nlevels(b$x2),col="white",xlab="",ylab="",axes=F,xlim=c(0,10.5),
ylim=c(0,10.5))
ct=c(3,3,2,1,1)
abline(v=.5+c(0,cumsum(ct)),lty=2)
abline(h=.5+c(0,cumsum(ct)),lty=2)
text(1:10,0,LETTERSord)
text(0,1:10,LETTERSord)
for(i in 1:nlevels(b$x2)){
#levels(b$x2)=LETTERS[1:10]
b$x2=relevel(b$x2,LETTERSord[i])
p=summary(lm(y~x1+x2,data=b))$coefficients[-(1:2),4]
names(p)=substr(names(p),3,3)
P[LETTERSord[i],names(p)]=p
p=P[LETTERSord[i],]
idx=which(p>.05)
points(((1:10))[idx],rep(i,length(idx)),pch=1,cex=2)
idx=which(p>.1)
points(((1:10))[idx],rep(i,length(idx)),pch=19,cex=2)
}
在這裡,我們得到以下資訊:

It looks like we have our combined categories...
實際上,使用另一種策略是可能的。我們從某種程度上說“A”。然後,我們將它與所有非顯著的不同級別合併起來。如果“B”不是其中之一,我們使用它作為新的參考。等
for(i in 1:nlevels(b$x2)){
if(LETTERS[i]%in%levels(b$x2)){
b$x2=relevel(b$x2,LETTERS[i])
p=summary(lm(y~x1+x2,data=b))$coefficients[-(1:2),4]
names(p)=substr(names(p),3,nchar(p))
idx=which(p>.05)
mix=c(LETTERS[i],names(p)[idx])
b$x2=recode(b$x2, paste("c('",paste(mix,collapse = "','"),"')='",paste(mix,collapse = "+"),"'",sep=""))
}}
最後的類別是:
table(b$x2)
A+I+H B+D+F C+G E J
46 82 35 23 14
使用以下回歸輸出:
summary(lm(y~x1+x2,data=b))
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.86407 0.03950 21.877 < 2e-16 ***
x1 1.99180 0.05323 37.417 < 2e-16 ***
x2B+D+F -0.21517 0.03699 -5.817 2.44e-08 ***
x2C+G -0.50545 0.04528 -11.164 < 2e-16 ***
x2E -0.83617 0.05128 -16.305 < 2e-16 ***
x2J -0.68398 0.06131 -11.156 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2008 on 194 degrees of freedom
Multiple R-squared: 0.8975,Adjusted R-squared: 0.8948
F-statistic: 339.6 on 5 and 194 DF, p-value: < 2.2e-16
AIC(lm(y~x1+x2,data=b))
[1] -66.76939
BIC(lm(y~x1+x2,data=b))
[1] -43.68117
這和我們以前的團隊是一致的。但實際上,如果我們改變順序,我們可以得到不同的組合。例如,如果我們從“J”到“A”,而不是“A”到“J”,我們得到:
for(i in nlevels(b$x2):1){
#levels(b$x2)=LETTERS[1:10]
if(LETTERS[i]%in%levels(b$x2)){
b$x2=relevel(b$x2,LETTERS[i])
p=summary(lm(y~x1+x2,data=b))$coefficients[-(1:2),4]
names(p)=substr(names(p),3,nchar(p))
idx=which(p>.05)
mix=c(LETTERS[i],names(p)[idx])
b$x2=recode(b$x2, paste("c('",paste(mix,collapse = "','"),"')='",paste(mix,collapse = "+"),"'",sep=""))
}}
table(b$x2)
E G+C I+A+B+D+F+H J
23 35 128 14
這裡有不同的資訊標準:
AIC(lm(y~x1+x2,data=b))
[1] -36.61665
BIC(lm(y~x1+x2,data=b))
[1] -16.82675
我想有必要隨機執行我們通過這些級別的順序。最後,但同樣重要的是,我們可以使用迴歸樹。問題是,還有另一個解釋變數可能會插入。所以我建議(1)擬合一個線性模型
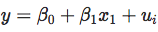
為了計算殘差,
![]()
(2)執行迴歸樹,解釋
![]()
使用範疇變數x_2(我解釋了樹是如何構建的,而解釋變數是以前的職位):
library(rpart)
library(rpart.plot)
b$e=residuals(lm(y~x1,data=b))
arbre=rpart(e~x2,data=b)
prp(arbre,type=2,extra=1)

觀察到葉子和我們得到的葉子是一樣的。
arbre
n= 200
node), split, n, deviance, yval
* denotes terminal node
1) root 200 22.563500 7.771561e-18
2) x2=G,C,J,E 72 4.441495 -3.232525e-01
4) x2=J,E 37 1.553520 -4.578492e-01 *
5) x2=G,C 35 1.509068 -1.809646e-01 *
3) x2=I,A,H,F,B,D 128 6.366628 1.818295e-01
6) x2=F,B,D 82 2.983381 1.048246e-01 *
7) x2=I,A,H 46 2.030229 3.190993e-01 *
我想應該可以把所有這些放在一個R函式中,建議可能改進迴歸的水平組合。
