刁肥宅詳解中綴表示式求值問題:C++實現順序/鏈棧解決
1. 表示式的種類
如何將表示式翻譯成能夠正確求值的指令序列,是語言處理程式要解決的基本問題,作為棧的應用事例,下面介紹表示式的求值過程。 任何一個表示式都是由運算元(亦稱運算物件)、操作符(亦稱運算子)和分界符組成的。通常,算術表示式有3種表示: ①中綴(infix)表示:<運算元><操作符><運算元>,如A+B。 ②字首(prefix)表示: <操作符><運算元><運算元>,如+AB。 ③字尾(postfix)表示: <運算元><運算元><操作符>,如AB+。
2. 求解演算法
在中綴表示式中操作符的優先順序和括號使得求值過程複雜化,把它轉換成字尾表示式,可以簡化求值過程。但是,老師使用的PPT上的示例顯然是直接對中綴表示式進行求值,並未進行轉換。因此我也採用“直接求值法”。為了實現對中綴表示式的求值,需要考慮各操作符的優先順序,參見表1。
| 操作符ch | # | ( | *、/、% | +、- | ) |
| isp | 0 | 1 |
5 | 3 | 6 |
| icp | 0 | 6 | 4 | 2 | 1 |
表1 各個運算子的優先順序
表中的isp叫做棧內優先順序(in stack priority),icp叫做棧外優先順序(in coming priority)。為什麼要如此設定呢?這是因為某一操作符按照算術四則運算有一個優先順序,這是icp。一旦它進入操作符棧,它的優先順序要提高,以體現優先順序相同的操作符先來的先做,就是說,在表示式中運算優先順序相同的必須自左向右運算,這就是棧內優先順序isp。
從上表可以看到,左括號“(”的棧外優先數最高,它一來到立即進棧,但當它進入棧中後,其棧內優先數變得極低,以便括號內的其他操作符進棧。除它之外,其他操作符進入棧中後優先數都升1,這樣可以體現中綴表示中相同優先順序的操作符自左向右計算的要求,讓位於棧頂的操作符先退棧輸出。操作符優先數相等的情況只出現在“(”與棧內“)”括號配對或棧底的“#”號與表示式輸入最後的“#”號配對時。前者將連續推出位於棧頂的操作符,直到遇到“)”為止。然後將“(”退棧以對消括號,後者將結束演算法。
掃描中綴表示式,並求值的演算法描述如下:
1)操作符棧初始化,將結束符“#”進棧;運算元棧初始化。然後讀入中綴表示式字元流中的首字元 ch。
2)重複執行以下步驟,直到 ch=“#”,同時棧頂的操作符也是“#”,停止迴圈。
①若 ch 是運算元,將壓入運算元棧,讀入下一個字元 ch。
②若 ch 是操作符,比較ch的優先順序 icp 和操作符棧當前棧頂的操作符 op 的優先順序 isp:
• 若 icp(ch)> isp(op),令ch進棧,讀入下一個字元ch。
• 若 icp(ch)≤ isp(op),退出運算數棧的兩個元素a和b計算:a op b,將計算結果壓入運算數棧中。
• 若 ch = “)”或 op = “(”,退出運算子棧的棧頂元素,讀入下一字元ch。
3)演算法結束,運算數棧的棧頂元素即為所求中綴表示式的結果。
以上演算法是我結合在資料上看到的關於中綴表示式轉換為字尾表示式的演算法,自己琢磨出來的。演算法的正確性有待證明,但實現在計算幾個樣例時,結果正誤均有。具體結果將在第四部分展示。
另外,我在部落格和《演算法導論》上都看到所謂“雙棧算術表示式求值演算法”的介紹與大概思路:
雙棧算術表示式求值演算法是由E.W.Dijkstra在上個世紀60年代發明的一個很簡單的演算法,用兩個棧【一個用來儲存運算子、一個用來儲存運算元】來完成對一個表示式的運算。其實整個演算法思路很簡單:
• 無視左括號
• 將運算元壓入運算元棧
• 將運算子壓入運算子棧
• 在遇到右括號的時候,從運算子棧中彈出一個運算子,再從運算元棧中彈出所需的運算元,並且將運算結果壓入運算元棧中
---------------------
作者:erzhanchen
來源:CSDN
原文:https://blog.csdn.net/erzhanchen/article/details/57421267
版權宣告:本文為博主原創文章,轉載請附上博文連結!
為了表示對原作者的尊重,我保留了“犯罪痕跡”。
3. 核心程式碼
在正式貼出核心程式碼(完整程式碼將寫在下一篇部落格)前先進行一些必要說明: ①從右向左掃描表示式字串; ②C型別的字串開始下標是0,字串的最後一個元素是“\0”;
| D | a | t | a | ' ' | S | t | r | u | c | t | u | r | e | '\0' |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
③假設“1”、“2”、“3”、“4”、“5”這五個數字組成一個十進位制的整數,從左到右依次是萬位數、千位數、百位數、十位數、個位數,那麼計算這個整數的表示式就是下面這樣的: 1×104 +2×103+3×102+4×101+5×100=12345
1 void SeqStack::calculate( char* Str )///C型別字串表示式為引數傳入方法中
2 {
3 charSeqStack css1;///css1 用作操作符棧
4 char ch1;///訪問操作符棧棧頂元素時,儲存棧頂元素
5 int i = 0;///用來儲存當前掃描的表示式位置
6 double a, b;///用來儲存臨時運算時呼叫物件棧棧頂的前兩個元素
7
8 int cnt = 0;///記錄字串中數字連續時的位數,即計算 10 的 n 次方時冪的指數
9 ///比方說:在讀入整數156時,讀“1”這個字元之前讀了兩個數字“5”、“6”,那麼讀1的時候,這個1就代表100的意思。
10 int temp = 0;///儲存掃描到的數值
11
12 while ( Str[i] != '\0' )///確定表示式的終止下標
13 {
14 i ++;
15 }///比方說:在掃描表示式“#1+1#”時,表示式字串字元最大下標是5,但是表示式終止下標是3
16 i = i - 2;///C型別字串下標從0開始,字串的最後一位是'\0'
17
18 ///從右向左掃描表示式,當 操作符棧不為空 或 未掃描到表示式的最左邊 時 迴圈
19 while( css1.topValue() != -1 || Str[i] != '#' )
20 {
21 char ch = Str[i];///讀取掃描到的當前字元
22 if ( isdigit(ch) )///利用C語言的庫函式 isdigit() 判斷字元 ch 是否為數字。
23 ///庫函式 isdigit() 宣告在標頭檔案 ctype.h 中
24 ///演算法步驟 2)的情況 ①,如果 ch 是數字就將其轉換為對應的十進位制數
25 {
26 temp = temp + pow( 10, cnt ) * int( ch - '0' );///類似於 m 進位制 轉換為 10 進位制數時的操作
27 /// C語言的 pow() 函式定義在 math.h 中,pow( 10, cnt ) 計算的是 10 的 cnt 次方
28 cnt ++;///位數增一
29 i --;///繼續向左掃描表示式
30 }
31 else///如果 ch 不是數字,是運算子
32 {
33 if (cnt)///C語言中非零值的表示式布林值都為真,如果這個表示式為真說明原來掃描到了表示式中的數值
34 {
35 push(temp);///將數值壓入運算元棧中,運算元棧是呼叫物件中的棧
36 temp = 0;///在未掃描到新的數字前置零
37 cnt = 0;///在未掃描到新的數字前位數置零
38 }
39 css1.getTop(ch1);///讀取操作符棧的棧頂
40 if ( ch1 == ')' && ch == '(' )///演算法步驟 2)的情況 ② 的第三種
41 {
42 css1.pop();///將運算子棧棧頂元素退出
43 i --;///繼續向左掃描表示式
44 continue;
45 }
46 if ( isp(ch1) < icp(ch) )///演算法步驟 2)的情況 ② 的第一種
47 {
48 css1.push(ch);///將當前掃描到的操作符 ch 壓入操作符棧
49 i --;
50 }
51 else if (isp(ch1) >= icp(ch))///演算法步驟 2)的情況 ② 的第三種
52 {
53 getTop(a);///獲取運算元棧棧頂元素
54 pop();///彈棧,以便獲取第二個元素
55 getTop(b);///獲取運算元棧棧頂元素
56 pop();///彈棧,已計算過不用再保留
57 push( doOperator( a, b, ch1 ) );///將計算結果壓入運算數棧中
58 css1.pop();///退棧,已使用過不再保留
59 }
60 }
61 }
62
63 if (cnt)///細節處理:防止以數字為結尾的字串,比方說 #1#,沒有這個判斷的話,輸入 #1# 時就會出錯:因為1沒有被壓入運算元棧中
64 {
65 push(temp);
66 }
67 /*
68 #1#
69 #1+1#
70 #2*2+3#
71 #(1)#
72 寫程式碼的時候就是按照讓這4個表示式都能正常執行的思路來寫的
73 */
74 }
4. 說明及其他
void SeqStack::calculate( char* Str ) 這個方法我原來放置的引數是兩個:charSeqStack& css1, charSeqStack& css2 , css1 是運算子棧,css2 是表示式棧。後面發現這麼實現的話只能處理一位數的四則運算。經過考量,決定用C語言型字串代替作為引數。
被呼叫函式在獲取C語言型陣列與字串時無法得知其長度,因此第一個while迴圈作用是確定表示式字串的長度。第二個while迴圈從右向左掃描字串,對每個ch判斷後按演算法進行相應的操作。
值得一提是,每掃描到一個數字,就通過表示式 temp = temp + pow( 10, cnt ) * int( ch - ‘0”); 將當前連續數字所表達的確切十進位制值計算出來,並儲存在臨時變數temp中。另外,變數cnt的作用是表示當前有幾個連續的數字。當數字連續終止時(如圖1所示),將計算結果temp壓入呼叫物件ss1的棧(即運算元棧)中。
最後展示一下程式的執行截圖並簡要說明:
控制檯第一行列印的數值為使用形如以下方式得到的結果:
cout << 200+500*(200+300)*600/709-400 << endl;
即第一個待求解表示式由C++表示式計算所得結果,以用於與實現得出的結果作比較。
第1次測試:
第一個待求解表示式實現得出的結果比由C++表示式計算的結果大1,錯誤。
第2次測試:
第一個待求解表示式實現得出的結果與由C++表示式計算的結果完全一致;
第4次測試: 第一個待求解表示式實現得出的結果比由C++表示式計算的結果大1582,錯誤。
綜上所述,實現用於計算一些表示式是正確可行的,而對於另外一些表示式則正確得出結果。另,由實現計算5/3*9與(5/3)*9的結果知:是否新增括號對實現能否正確計算表示式有直接關係;對於不能正確計算的表示式,不同編譯器生成的可執行檔案得到的結果也不同(如圖7與圖8所示)。 “棧的應用:字尾表示式求值”演算法的實現還是有bug。
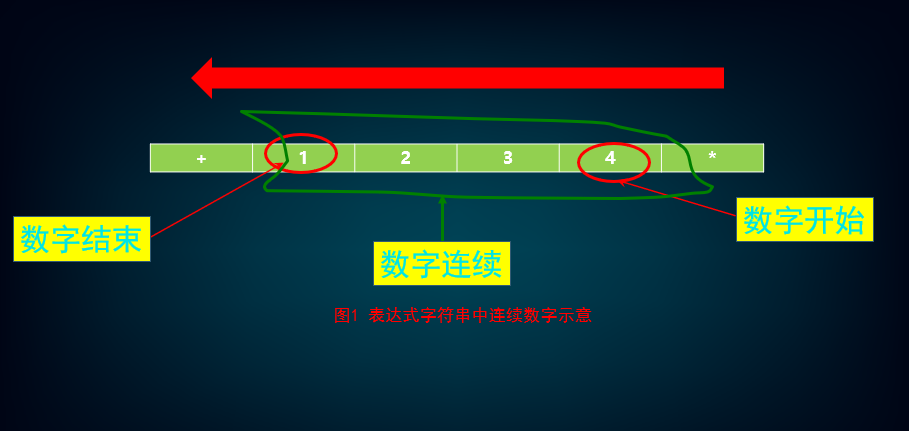
圖1 表示式字串中連續數字示意

圖3 求解111+56*(789+29)*5/80-400與12+5*(2+3)*6/2-4程式執行截圖
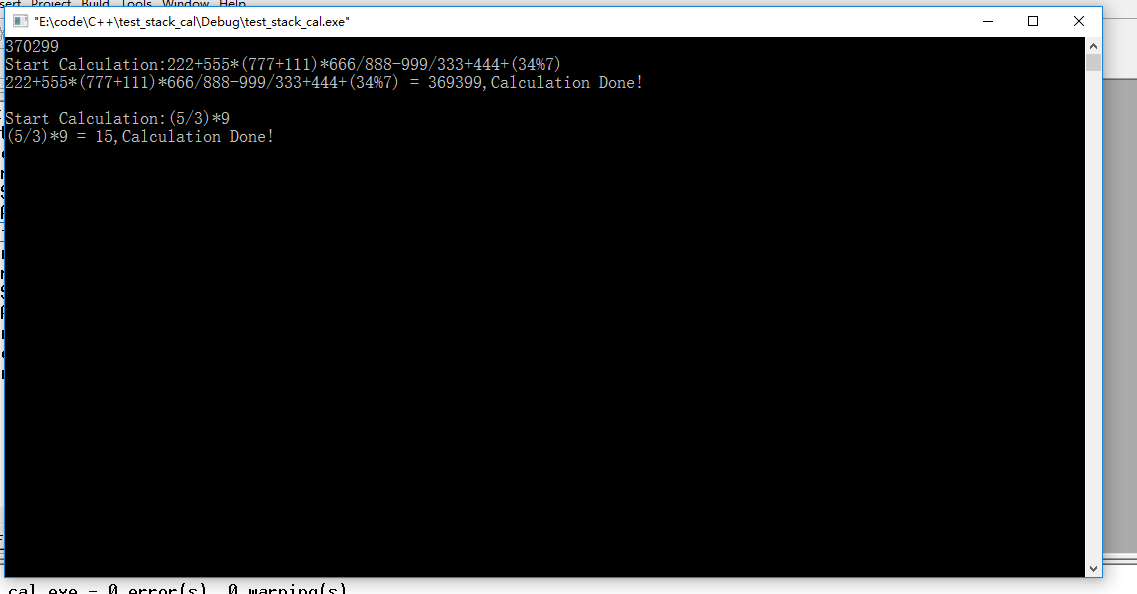
圖4 求解222+555*(777+111)*666/888-999/333+444+(34%7)與(5/3)*9程式執行截圖
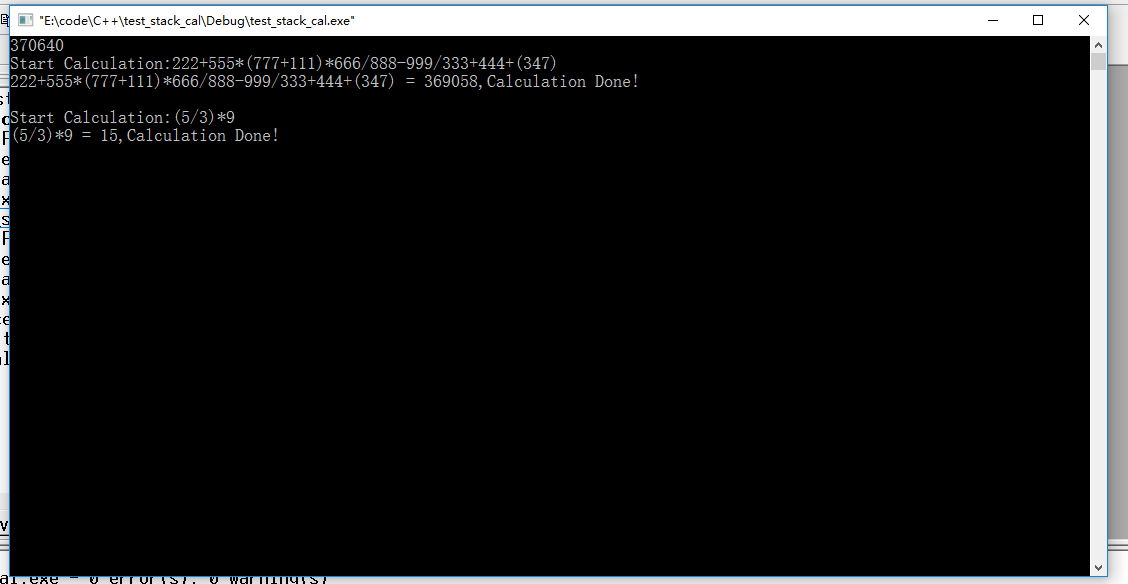
圖5 求解222+555*(777+111)*666/888-999/333+444+(347)與(5/3)*9程式執行截圖
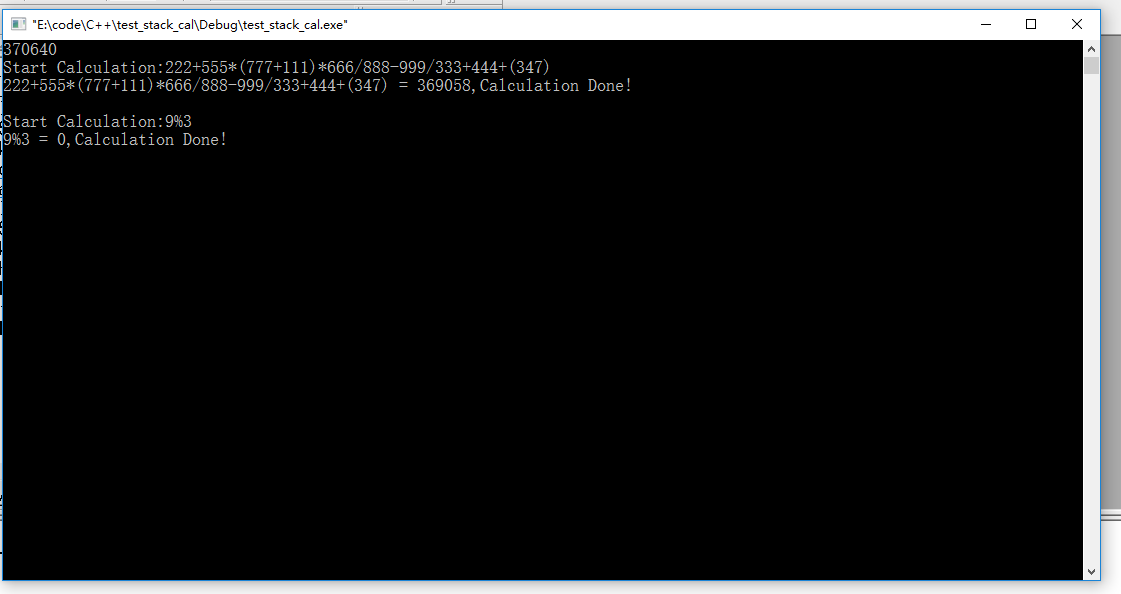
圖6 計算222+555*(777+111)*666/888-999/333+444+(347)與9%3程式執行截圖

圖7 Code::Blocks 17.12 編譯的可執行檔案計算200+500*(200+300)*600/709-400程式執行截圖

圖8 VC6.0 編譯的可執行檔案計算200+500*(200+300)*600/709-400程式執行截圖

圖9 計算12+5*(2+3)*6/2-4時運算元棧與操作符棧的變換情況
