巨集觀經濟學(1-4)
國民經濟核算
交易不改變 GDP,除非收手續費
儲蓄減投資等於預算赤字減貿易赤字
二手貨的出售不計入當期 GDP,因為在其生產的時候已計入 GDP,當期只是資產的轉移而非收入增加。當期變質存貨的不計入,但以後銷售的計入。
NNP = GNP - 折舊
PCE(個人消費支出)平減指數的特徵是 CPI 與 GDP 平減指數的混合,只包含消費者購買產品和服務的價格,因此包含進口品的價格;又給不嘔吐那個產品分配變動的權重。
失業率 = 失業者 / ( 失業者 + 就業者 )
勞動力參與率 = ( 失業者 + 就業者 ) / ( 成年人 )(成年人包括不屬於勞動者的人)
索洛模型(新古典增長模型,外生增長模型)
生產函式
規模報酬不變, 與
無關:
競爭性經濟中, ,
為常量:
其中 和
分別為勞動者報酬和資本所得佔 GDP 份額,
為常數,由此便可知
。
因為
為全要素生產率的增長率。在增長核算中,是由
得到
,稱為索洛剩餘。
全要素生產率不僅僅是技術,也有人力資本等因素。但在下文,只考慮技術,並只考慮技術為勞動增進型 ,即技術進步不改產出與資本之間的關係。顯然此處
的內涵發生了變化。可以推出
或
。
假定產出是資本與有效勞動 的一次齊次函式,則有效勞動的人均產出
其中
。
穩態定義為 ,於是
。由於邊際產量遞減,此方程一定有非零解。由於方程所有量均不含時間,所以方程的解
為關於時間的常數,由此可知
亦為常數。於是穩態增長率
,
,
。
下面考慮儲蓄率的影響。人均消費最大時,居民的福利最好。這要求 ,稱為黃金法則。穩態不一定符合黃金法則。當符合時,解微分方程,
,
為常數。儲蓄率對人均產量、消費和投資的影響如下。
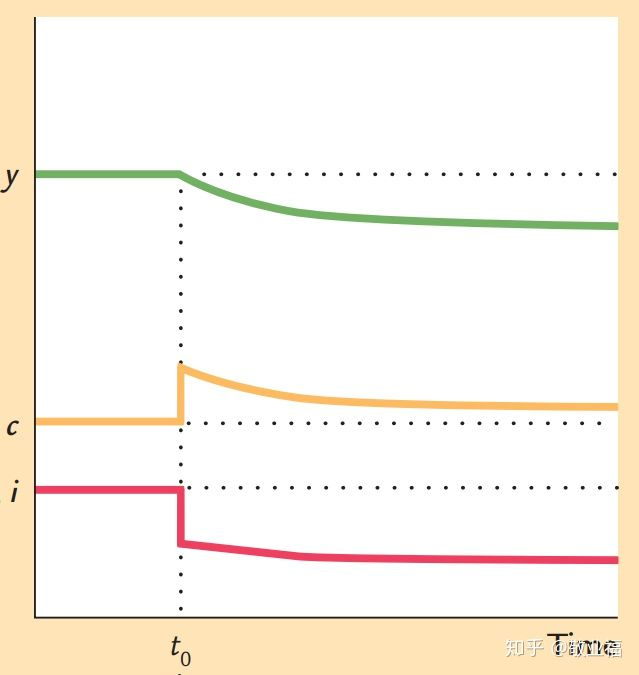
初始條件人均資本大於黃金律水平
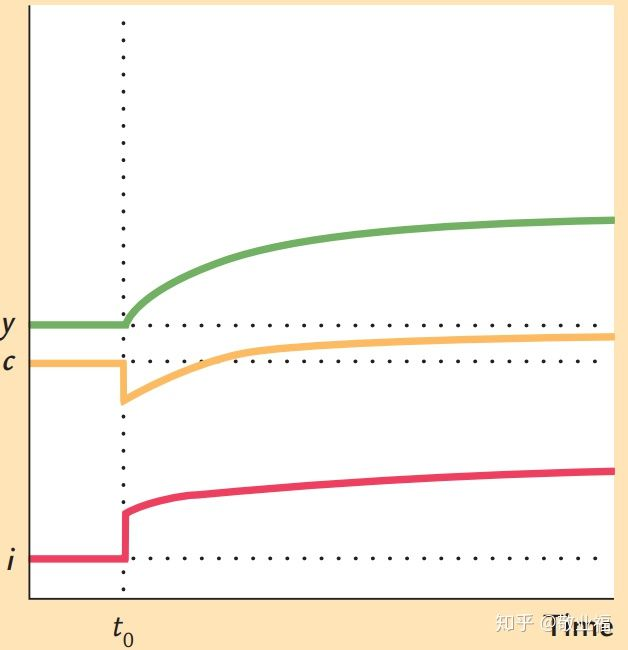
初始條件人均資本小於黃金律水平
內生增長理論
索洛模型中,長期增長率只取決於人口增長和技術進步,政策無法改變增長率。特別是,儲蓄率有水平效應,其增長效應只是暫時的。這當中最根本的原因是邊際產量遞減。現去除此假定,認為資本的邊際產量不變,那麼規模報酬遞增。這是因為保持勞動力不變,資本翻番就會使得產量翻番;現在勞動力也翻番,那麼總的效果就是產量不止是翻番。但是,規模報酬遞增難道不會導致世界上只剩下一個壟斷廠家嗎?答案是不會。因為這裡的“報酬”還包括了易於“外溢”的技術進步,也就是說報酬並不是由單個廠家私人獨佔的,因此也就不會形成壟斷。這個模型中,技術進步不再是外生的,而是包含在邊際產量不變的假設之中。
只要 ,經濟就一直增長。特別是,提高儲蓄率,有助於提高增長率。然而,經驗證據對此支援不足。
兩個增長模型的不同還表現在:索洛模型中人口增長率對人均產量增長率無影響,隻影響人均產量水平,而內生增長理論中降低人口增長率可以提高人均產量增長率,;索洛模型可以解釋觀察到的條件趨同,但內生增長理論不能解釋國際差異。

降低人口增長率有助於避免貧困陷阱(B)
總結:對於 、
、
,索洛模型——水平效應而無增長效應;內生增長理論——增長效應而無水平效應。
