第7章 小世界網路模型：
本章將圍繞小世界網路模型展開，主要內容分為兩個部分：
（1）如何構建具有較大的聚類特性又具有較短的平均距離的小世界網路模型？
（2）什麼樣的小世界網路才能實現有效搜尋？

7.2小世界網路模型

7.2.1小世界網路模型
完全規則最近耦合網路：
高聚類：c=3(k-2)/4(k-1)>=3/8;
平均路徑長度：N/2K
完全隨機的er圖：
沒有高聚類：
具有小的平均路徑長度：
Cer=K/N-1

於是，規則的最近網路和er隨機圖都不能再現實際網路同時具有的明顯聚類和小世界特徵：

然後watts發現：作為從完全規則網路向完全隨機網路的過渡：只要在規則網路中引入少許的隨機性就可以產生具有小世界特徵的網路模型，現在常稱為ws小世界模型：

演算法7-1 ws小世界模型構造演算法
（1）從規則圖開始：給定一個含有N個點的環狀最近鄰耦合網路，其中每個節點都與它左右相鄰的各K/2個節點相連，k是偶數
（2）隨機化重連：以概率p隨機地重新連線網路中原有的每條邊，即把每條邊的一個端點保持不變，另一個端點改取為網路中隨機選擇的一個節點。其中規定不得有重邊和自環。

[注意]p=1的情形下，演算法得到的ws小世界模型與er隨機圖還是有很大的區別的，因為ws小世界模型中每一個節點的度至少為K/2,而在er隨機圖中對單個節點的度的最小值沒有任何的限制。

7.2.2模擬分析

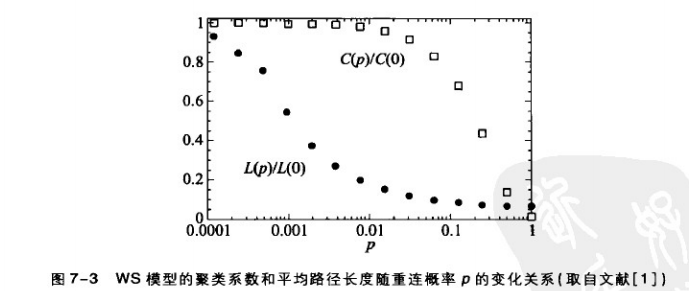
當p開始增大時，隨機重連後的網路的聚類係數下降緩慢但平均路徑長度下降很快

這意味著，當重連概率p較小時，網路既具有較短的平均長度又具有較高的聚類係數

通過上面的圖我們所學到的科學的處理方法：

（1）歸一化處理：
（2）對數化座標：採用對數座標的好處就是可以在橫軸上把較小p值的刻度拉寬較大p值的區間
（3）平均化處理：考慮隨機性
從圖中我們可以知道：當重連概率p較小時，網路既具有較短的平均路徑長度又具有較高的聚類係數。

7.2.3實際驗證：
實際的網路有如下的共同特徵：La稍大於Lr，但是Ca遠大於Cr！

7.2.4動力學分析

ws小世界模型上的病毒傳播動力學體現了網路科學研究的一種正規化：

（1）建立模型
（2）模擬分析
（3）實際驗證
（4）影響分析

在ws模型提出之後，人又提出了另一個在理論分析方面相對容易處理的小世界模型，現在稱為nw小世界模型。
演算法：
（1）從規則圖開始：給定一個含有N個節點的環狀最近鄰耦合網路，其中每個節點都與它左右相鄰的各K/2個節點相連，K是偶數
（2）隨機化加邊：以概率P在隨機選取的Nk/2對節點之間新增邊，其中規定不得有重邊和自環

總結
小世界模型反映了朋友關係網路的一種特性，即你的大部分朋友都說和你住在同一條街上的鄰居或在同一單位工作的同事。另一方面，也有一些人是比較遠的，這就是對應ws模型中的重新連邊或者nw小世界模型中的隨機加邊。

7.3 拓撲性質分析

本節主要從理論上分析小世界模型的3個拓撲性質：聚類係數，平均路徑長度和度分佈

7.3.1聚類係數

1.ws小世界網路

網路中度為Ki的節點i的聚類係數Ci定義為：

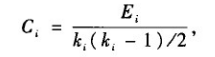
聚類係數的估值為：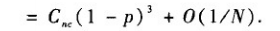

從下圖中可以看出聚類係數與p是單調遞減的關係，意味著隨機性的增強，網路的聚類係數效應減弱。

1.nw小世界網路

（推導太煩了，沒看懂）

 7.3.2平均路徑長度：

小世界模型的平均長度應該具有如下的形式：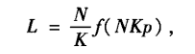

其中F（u）為一與模型引數無關的普適標度函式
經過一系列的推導可得：

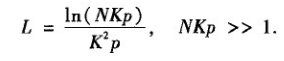
這個式子表名只要網路中隨機新增的邊數足夠多，那麼平均路徑長度就可以視為網路規模的對數增長函式。

 7.3.3度分佈：

1.ws小世界模型的度分佈：

可以看出，p值越大，然後度分佈也就越廣泛

2.nw小世界模型

當網路中節點數N足夠大時，度分佈可近似為下面的式子：

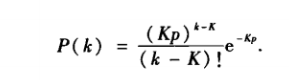
7.4 Kleinberg模型與可搜尋性：

儘管連線兩個人的路徑的數目可能很大，而且不同路徑的長度的差異性也可能很大，人們還是可能用簡單的分散式演算法找到連線自己與陌生人之間的較短的路徑。

milgram的小世界實驗比較簡單，使用的是貪婪演算法

但是，一般而言，網路的小世界特性並不意味這網路是可以快速搜尋的。如何找到任意兩個節點之間的較短的路徑依賴於搜尋問題的定義，節點提供的網路結構資訊，節點使用的搜尋演算法和整個網路的拓撲結構。

（1）問題定義：隨機選擇的節點s和t如何考慮最少的步數將資訊從s傳遞帶目標節點t。
（2）節點提供的區域性資訊：當前節點只知道目標節點在網路上的位置和節點之間的區域性連線路徑。
（3）搜尋演算法：貪婪演算法

由此產生的問題：
什麼樣的小世界網路是可搜尋的， 是否存在最短的平均傳遞步數的最優網路結構？
為了描述這一問題，將網路模型從一維環狀推廣到二維網格上。網格中兩個節點u v距離為d（u，v）=|k-i|+|l-j。

Kleinberg對二維nw小世界做了如下的修改：

（1）每條邊都是有向邊
（2）假設長程連線並不是完全隨機的新增到原先的規則網路中，節點u有邊指向節點v的概率與這兩個節點之間的網路距離的冪函式[d（u，v）-阿法]成正比

當a值很大時，新增的邊幾乎都成為了短程連線。
當a值很小時，新增的邊過於隨機，幾乎就是nw小世界。

是否存在規則性和隨機性之間的最佳折中，使得生產的網路即是小世界又便於快速分散式搜尋？

最優網路結構

kleinberg進一步從理論上嚴格證明了 當N->無窮大時，阿法=2是唯一的最優值。

具體的說，對於任意一個給定的階段，可以將網格中其他節點歸於集合Ao，其中Aj包含了所有與節點u的網格距離在區間p[2j，2j+1]內的節點。在a=2時，節點u的每個新增的長程連線的邊落在集合Aj中的概率幾乎都是相等的，a<2時，新增的連線的另一端點偏向於那些網路距離比較大的集合；當a>2時，新增的連線的另一個端點偏向於那些網格距離比較小的集合。

7.4.3 kleinberg模型的理論分析

 我們需要證明的是當a=1時候，基於區域性資訊的貪婪演算法所需的路徑仍然是非常短的。

7.4.4線上網路實驗驗證

在kleinberg模型中有兩個基本假設：

（1）兩個節點存在長程連線的概率是由它們之間的網格距離決定的
（我想到一個方向，如果我新增一個“人情因素”是在kleinberg模型基礎上新增的是不是使得這樣的模型更加的科學呢？）
（2）所有節點在空間上是均勻分佈的：
而在實際問題中
（1）短距離中，地理因素佔據著主導因素
（2）長距離中，非地理因素佔據著主導地位

於是livejournal提出了基於zhi的二維經緯模型：

（我覺得livejournal模型就是基於“人情”的）

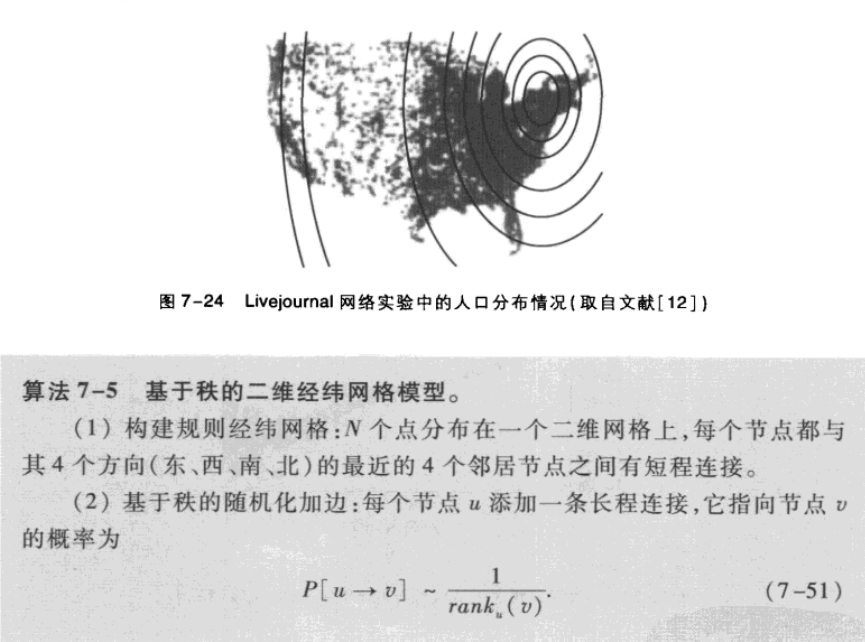
上述研究表明：
（1）從可搜尋角度來看，kleinberg僅考慮地理因素對長程連線的影響是合理的，也就是說，在這樣的理論模型下是可以找到較短路徑的。
（2）從最優化的角度看，基於zhi的模型可能更加的符合實際。