第3章 遞迴

1、基本遞迴

假設想計算整數n的階乘，比如4！=4×3×2×1。

迭代法：迴圈遍歷其中的每一個數，然後與它之前的數相乘作為結果再參與下一次計算。可正式定義為：n! = (n)(n-1)(n-2)…(1)。

遞迴法：將n!定義為更小的階乘形式。可以正式定義為：

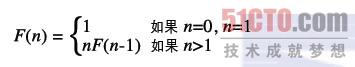
遞迴過程中的兩個基本階段：遞推與迴歸。

遞推階段，每一個遞迴呼叫通過進一步呼叫自己來記住這次遞迴過程。當其中有呼叫滿足終止條件時，遞推結束。每一個遞迴函式都必須擁有至少一個終止條件；否則，遞推階段就永遠不會結束了。一旦遞推階段結束，處理過程就進入迴歸階段，在這之前的函式呼叫以逆序的方式迴歸，直到最初呼叫的函式返回為止，此時遞迴過程結束。

 示例3-1：以遞迴方式計算階乘的函式實現

/* fact.c */   
#include "fact.h"  
/* fact */  
int fact(int n) {  
if (n < 0)  
   return 0;  
else if (n == 0)  
   return 1;  
else if (n == 1)  
   return 1;  
else  
   return n * fact(n - 1);  
} 

補充知識點 ： C程式在記憶體中的組織方式

基本上來說一個可執行程式由4個區域組成：程式碼段、靜態資料區、堆與棧

　　1）程式碼段：包含程式執行時所執行的機器指令；

　　2）靜態資料區：包含在程式生命週期內一直持久的資料，如全域性變數和靜態區域性變數；

　　3）堆：包含程式執行時動態分配的儲存空間，比如用malloc分配的記憶體；

　　4）棧：包含函式呼叫的資訊。

按照慣例，堆的增長方向為從程式低地址到高地址向上增長，而棧的增長方向剛好相反（實際情況可能不是這樣，與CPU的體系結構有關）。

注意：此處的堆與資料結構中的堆沒有什麼關係。

圖3-2：a）C程式在記憶體中的組織形式  b）一份活躍記錄

當C程式中呼叫了一個函式時，棧

棧幀由5個區域組成（見圖3-2b）：

　　1）輸入引數：傳遞到活躍記錄中的引數

　　2）返回值空間：

　　3）計算表示式時用到的臨時儲存空間：

　　4）函式呼叫時儲存的狀態資訊：

　　5）輸出引數：傳遞給在活躍記錄中呼叫的函式所使用的引數。

一個活躍記錄中的輸出引數就成為棧中下一個活躍記錄的輸入引數。函式呼叫產生的活躍記錄將一直存在於棧中直到這個函式呼叫結束。

回到示例3-1，考慮一下當計算4!時棧中都發生了些什麼。

初始呼叫fact會在棧中產生一個活躍記錄，輸入引數n=4（見圖3-3，第1步）。

由於這個呼叫沒有滿足函式的終止條件，因此fact將繼續以n=3為引數遞迴呼叫。這將在棧上建立另一個活躍記錄，但這次輸入引數（見圖3-3，第2步）。這裡，n=3也是第一個活躍期中的輸出引數，因為正是在第一個活躍期內呼叫fact產生了第二個活躍期。

這個過程將一直繼續，直到n的值變為1，此時滿足終止條件，fact將返回1（見圖3-3，第4步）。

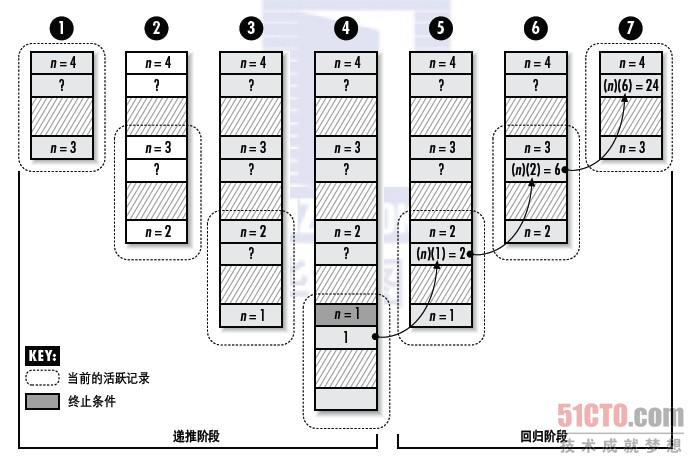
圖3-3：遞迴計算4!時的C程式的棧

棧是用來儲存函式呼叫資訊的絕好方案，這歸功於其後進先出的特點滿足了函式呼叫和返回的順序。然而，使用棧也有一些缺點。

　　1）棧維護了每個函式呼叫的資訊直到函式返回後才釋放，佔用空間大，尤其是在程式中遞迴呼叫很多的情況下。

　　2）因有大量的資訊需儲存和恢復，故生成和銷燬活躍記錄需要耗費一定的時間。

解決方法：可以採用一種稱為尾遞迴的特殊遞迴方式來避免前面提到的這些缺點。

2、尾遞迴

若一個函式中所有遞迴形式的呼叫都出現在函式的末尾，則稱該遞迴函式是尾遞迴的。

當遞迴呼叫是整個函式體中最後執行的語句，且它的返回值不屬於表示式的一部分時，該遞迴呼叫就是尾遞迴。

尾遞迴函式的特點是：在迴歸過程中不用做任何操作，大多數現代的編譯器會利用該特點自動生成優化的程式碼。

當編譯器檢測到一個函式呼叫是尾遞迴時，它就覆蓋當前的活躍記錄，而不是在棧中去建立一個新的，從而將所使用的棧空間大大縮減，這使得實際的執行效率會變得更高。因此，只要有可能我們就需要將遞迴函式寫成尾遞迴的形式。

之前對計算n!的定義：在每個活躍期計算n倍的(n－1)!的值，讓n=n－1並持續這個過程直到n=1為止。這種定義不是尾遞迴的，因為每個活躍期的返回值都依賴於用n乘以下一個活躍期的返回值，因此每次呼叫產生的棧幀將不得不儲存在棧上直到下一個子呼叫的返回值確定。

以尾遞迴的形式來定義計算n!的過程，函式可定義為以下形式：

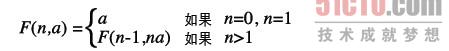
圖3-4說明了用尾遞迴計算4!的過程。

注意在迴歸的過程中不需要做任何操作，這是所有尾遞迴函式的標誌。

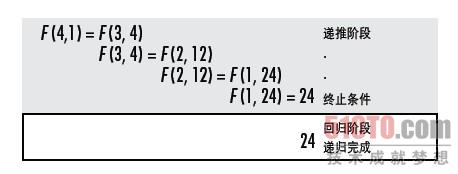
圖3-4：以尾遞迴的方式計算4!

示例3-2：以尾遞迴的形式計算階乘的一個函式實現

/* facttail.c */                                                                                                                                   
#include "facttail.h"  
/* facttail  */  
int facttail(int n, int a) {  
/* Compute a factorial in a tail-recursive manner. */  
if (n < 0)  
   return 0;  
else if (n == 0)  
   return 1;  
else if (n == 1)  
   return a;  
else  
   return facttail(n - 1, n * a);  
}

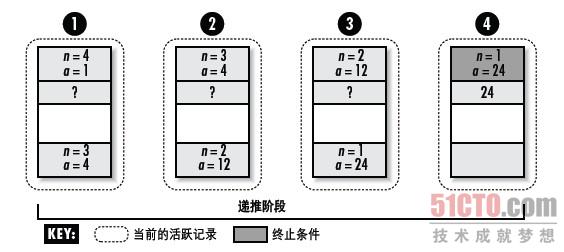
圖3-5：以尾遞迴形式計算4!時棧的情況

3、問與答

問：以下遞迴定義中有錯誤，請指正。歸併排序將一組資料一分為二，然後分別將兩份資料各自再進行分半處理，一直持續這個過程直到每一份都只含一個元素。然後在迴歸過程中完成各份資料的合併最終產生一個有序的集合。

答：該定義的問題在於當n的初始值大於0時將永遠無法滿足終止條件n=0。為了解決問題，需要一個滿足要求的終止條件。n－1這個條件就能很好滿足，這意味著也要修改函式中的第二個條件。合適的遞迴定義應該是這樣的：

問：以遞迴的思想描述一種求解整數質因子的方法。分析該方法是否是尾遞迴的並解釋原因。

答：遞迴是一種求解整數質因子的很自然的方法，因為因子分解無非就是不斷地解決同樣的問題。每當確定了一個因子，剩餘因子的集合就變得越來越小。針對這個問題的遞迴方法可以定義為如下式子：

這個定義的意思是說：為了遞迴地確定整數n的質因子，先確定它的最小質因子i並把它記錄到集合P中，然後對整數n=n/i重複這個過程直到n本身成為質數為止，這就是終止條件。這個定義是尾遞迴的，因為在迴歸過程中不需要做任何處理，如圖3-6所示。

圖3-6：以尾遞迴的方式計算整數2409的質因子

問：思考當執行遞迴函式時棧的使用情況，當遞迴過程的遞推階段永遠不會終止時會出現什麼情況？

答：如果遞迴函式的終止條件永遠得不到滿足，最終棧的增長會超過可接受的值，程式會因為棧溢位而終止執行。當程式執行時，一個稱為幀指標的特殊指標會定址棧頂的幀。正是棧指標指向實際的棧頂（即，下一個棧幀將被壓入的位置。因此，雖然某個系統可能使用來判斷棧溢位，但是它可能是通常會使用的棧指標。）