【音訊】G711編碼原理
1、熟悉G711a/u兩種格式的基本原理
2、熟悉兩種壓縮演算法的實現步驟及提供原始碼實現
G711的內容是將14bit(uLaw)或者13bit(aLaw)取樣的PCM資料編碼成8bit的資料流,播放的時候在將此8bit的資料還原成14bit或者13bit進行播放,不同於MPEG這種對於整體或者一段資料進行考慮再進行編解碼的做法,G711是波形編解碼演算法,就是一個sample對應一個編碼,所以壓縮比固定為:
8/14 = 57% (uLaw)
8/13 = 62% (aLaw)
G.711就是語音模擬訊號的一種非線性量化, bitrate 是64kbps. 詳細的資料可以在ITU 上下到相關的spec,下面主要列出一些效能引數:
G.711(PCM方式)
• 取樣率:8kHz
• 資訊量:64kbps/channel
• 理論延遲:0.125msec
• 品質:MOS值4.10
演算法原理:
A-law的公式如下,一般採用A=87.6
畫出圖來則是如下圖,用x表示輸入的取樣值,F(x)表示通過A-law變換後的取樣值,y是對F(x)進行量化後的取樣值。
由此可見在輸入的x為高值的時候,F(x)的變化是緩慢的,有較大範圍的x對應的F(x)最終被量化為同一個y,精度較低。相反在低聲強區域,也就是x為低值的時候,F(x)的變化很劇烈,有較少的不同x對應的F(x)被量化為同一個y。意思就是說在聲音比較小的區域,精度較高,便於區分,而聲音比較大的區域,精度不是那麼高。
對應解碼公式(即上面函式的反函式):
G711A(A-LAW)壓縮十三折線法
g711a輸入的是13位(S16的高13位),這種格式是經過特別設計的,便於數字裝置進行快速運算。
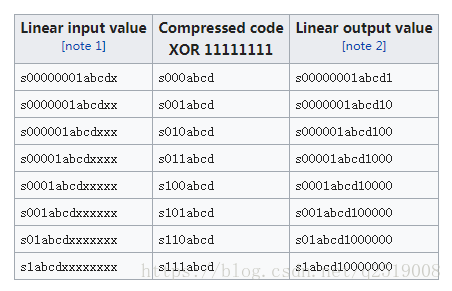
A-law如下表計算,第一列是取樣點,共13bit,最高位為符號位。對於前兩行,折線斜率均為1/2,跟負半段的相應區域位於同一段折線上,對於3到8行,斜率分別是1/4到1/128,共6段折線,加上負半段對應的6段折線,總共13段折線,這就是所謂的A-law十三段折線法。
示例:
輸入pcm資料為1234,二進位制對應為(0000 0100 1101 0010)
二進位制變換下排列組合方式(0 00001 0011 010010)
1、獲取符號位最高位為0,取反,s=1
2、獲取強度位00001,查表,編碼制應該是eee=011
3、獲取高位樣本wxyz=0011
4、組合為10110011,逢偶數為取反為11100110,得到E6
#define SIGN_BIT (0x80) /* Sign bit for a A-law byte. */
#define QUANT_MASK (0xf) /* Quantization field mask. */
#define NSEGS (8) /* Number of A-law segments. */
#define SEG_SHIFT (4) /* Left shift for segment number. */
#define SEG_MASK (0x70) /* Segment field mask. */
static int seg_aend[8] = {0x1F, 0x3F, 0x7F, 0xFF,
0x1FF, 0x3FF, 0x7FF, 0xFFF};
static int seg_uend[8] = {0x3F, 0x7F, 0xFF, 0x1FF,
0x3FF, 0x7FF, 0xFFF, 0x1FFF};
static int search(
int val, /* changed from "short" *drago* */
int * table,
int size) /* changed from "short" *drago* */
{
int i; /* changed from "short" *drago* */
for (i = 0; i < size; i++) {
if (val <= *table++)
return (i);
}
return (size);
}
int linear2alaw(int pcm_val) /* 2's complement (16-bit range) */
/* changed from "short" *drago* */
{
int mask; /* changed from "short" *drago* */
int seg; /* changed from "short" *drago* */
int aval;
pcm_val = pcm_val >> 3;//這裡右移3位,因為取樣值是16bit,而A-law是13bit,儲存在高13位上,低3位被捨棄
if (pcm_val >= 0) {
mask = 0xD5; /* sign (7th) bit = 1 二進位制的11010101*/
} else {
mask = 0x55; /* sign bit = 0 二進位制的01010101*/
pcm_val = -pcm_val - 1; //負數轉換為正數計算
}
/* Convert the scaled magnitude to segment number. */
seg = search(pcm_val, seg_aend, 8); //查詢取樣值對應哪一段折線
/* Combine the sign, segment, and quantization bits. */
if (seg >= 8) /* out of range, return maximum value. */
return (0x7F ^ mask);
else {
//以下按照表格第一二列進行處理,低4位是資料,5~7位是指數,最高位是符號
aval = seg << SEG_SHIFT;
if (seg < 2)
aval |= (pcm_val >> 1) & QUANT_MASK;
else
aval |= (pcm_val >> seg) & QUANT_MASK;
return (aval ^ mask);
}
}int alaw2linear(int a_val)
{
int t; /* changed from "short" *drago* */
int seg; /* changed from "short" *drago* */
a_val ^= 0x55; //異或操作把mask還原
t = (a_val & QUANT_MASK) << 4;//取低4位,即表中的abcd值,然後左移4位變成abcd0000
seg = ((unsigned)a_val & SEG_MASK) >> SEG_SHIFT; //取中間3位,指數部分
switch (seg) {
case 0: //表中第一行,abcd0000 -> abcd1000
t += 8;
break;
case 1: //表中第二行,abcd0000 -> 1abcd1000
t += 0x108;
break;
default://表中其他行,abcd0000 -> 1abcd1000 的基礎上繼續左移(按照表格第二三列進行處理)
t += 0x108;
t <<= seg - 1;
}
return ((a_val & SIGN_BIT) ? t : -t);
}u-law也叫g711u,使用在北美和日本,輸入的是14位,編碼演算法就是查表,計算出:基礎值+平均偏移值 沒啥複雜演算法,就是基礎值+平均偏移值,
μ-law的公式如下,μ取值一般為255
相應的μ-law的計算方法如下表

示例:
輸入pcm資料為1234
1、取得範圍值,查表得 +2014 to +991 in 16 intervals of 64
2、得到基礎值為0xA0
3、得到間隔數為64
4、得到區間基本值2014
5、當前值1234和區間基本值差異2014-1234=780
6、偏移值=780/間隔數=780/64,取整得到12
7、輸出為0xA0+12=0xAC
#define BIAS (0x84) /* Bias for linear code. 線性碼偏移值*/
#define CLIP 8159 //最大量化級數量
int linear2ulaw( int pcm_val) /* 2's complement (16-bit range) */
{
int mask;
int seg;
int uval;
/* Get the sign and the magnitude of the value. */
pcm_val = pcm_val >> 2;
if (pcm_val < 0) {
pcm_val = -pcm_val;
mask = 0x7F;
} else {
mask = 0xFF;
}
if ( pcm_val > CLIP ) pcm_val = CLIP; /* clip the magnitude 削波*/
pcm_val += (BIAS >> 2);
/* Convert the scaled magnitude to segment number. */
seg = search(pcm_val, seg_uend, 8);
/*
* Combine the sign, segment, quantization bits;
* and complement the code word.
*/
if (seg >= 8) /* out of range, return maximum value. */
return (0x7F ^ mask);
else {
uval = (seg << 4) | ((pcm_val >> (seg + 1)) & 0xF);
return (uval ^ mask);
}
}
int ulaw2linear( int u_val)
{
int t;
/* Complement to obtain normal u-law value. */
u_val = ~u_val;
/*
* Extract and bias the quantization bits. Then
* shift up by the segment number and subtract out the bias.
*/
t = ((u_val & QUANT_MASK) << 3) + BIAS;
t <<= (u_val & SEG_MASK) >> SEG_SHIFT;
return ((u_val & SIGN_BIT) ? (BIAS - t) : (t - BIAS));
}
以上是兩種演算法的連續條件下的計算公式,實際應用中,我們確實可以用浮點數計算的方式把F(x)結果計算出來,然後進行量化,但是這樣一來計算量會比較大,實際上對於A-law(A=87.6時),是採用13折線近似的方式來計算的,而μ-law(μ=255時)則是15段折線近似的方式。
參考:
https://en.wikipedia.org/wiki/A-law_algorithm
https://github.com/quatanium/foscam-ios-sdk/blob/master/g726lib/g711.c
https://www.cnblogs.com/charybdis/p/8848457.html