深度學習之PyTorch實戰（3）——實戰手寫數字識別

　　上一節，我們已經學會了基於PyTorch深度學習框架高效，快捷的搭建一個神經網路，並對模型進行訓練和對引數進行優化的方法，接下來讓我們牛刀小試，基於PyTorch框架使用神經網路來解決一個關於手寫數字識別的計算機視覺問題，評價我們搭建的模型的標準是它是否能準確的對手寫數字圖片進行識別。

　　其具體的過程是：先使用已經提供的訓練資料對搭建好的神經網路模型進行訓練並完成引數優化，然後使用優化好的模型對測試資料進行預測，對比預測值和真實值之間的損失值，同時計算出結果預測的準確率。在將要搭建的模型中會使用到卷積神經網路模型，下面讓我們開始學習吧。

知識儲備——深度學習中的常見概念

1：MNIST資料集的瞭解

　　MNIST資料集是一個已經被“嚼爛”了的資料集，很多教程都會對他“下手”，幾乎成為了一個典範。

　　具體詳情請參考 Yann LeCun's MNIST page 或 Chris Olah's visualizations of MNIST.

　　下載下來的檔案如下：

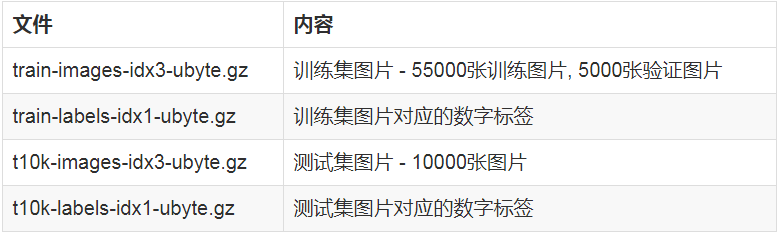
　　可從該頁面獲得的MNIST手寫數字資料庫具有60,000個示例的訓練集和10,000個示例的測試集。它是NIST提供的更大集合的子集。數字已經過尺寸標準化，並以固定尺寸的影象為中心。

　　對於那些希望在實際資料上嘗試學習技術和模式識別方法，同時在預處理和格式化方面花費最少的人來說，它是一個很好的資料庫。

2：梯度遞減演算法

　　在對決策函式進行優化的時候，通常是針對一個誤差的度量，比如誤差的平方，以求得一系列引數，從而最小化這個誤差度量的值來進行的，而目前一般採用的計算方法是梯度遞減法（Gradient Descent Method ）。這是一個非常形象的名字，好比一個遊客要從某個不知名的高山上儘快，安全的下到谷底，這時候需要藉助指南針來引導方向。對於這個遊客，他需要在南北和東西兩個軸向上進行選擇，以保證下山的路在當前環境下即使最快的，又是最安全的。我們可以將南北和東西兩個軸向想象成目標函式裡面的兩個維度或者自變數。那麼這個遊客怎麼獲取這個最優的路徑呢？

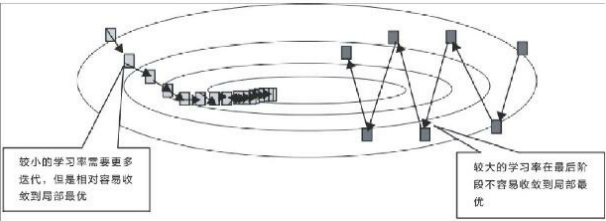
　　在山頂的時候，遊客因為不能完全看到通往谷底的情況，所以很可能隨機選擇一條路線。這個選擇很多時候很關鍵。一般山頂是一塊平地，有多個可以選擇下山的可能點。如果真正下山的路線是在某個地方，而遊客選擇了另外一個地方，則很有可能最終到不了真正的谷底，可能到達半山腰或者山腳下的某一個地方，但是離真正的谷底差距可能不小。這就是優化問題中的由於初始化引數不佳導致只能獲取區域性最優解的情況，下圖就形象的展示了這樣的情況。

在優化演算法中初始值的影響

　　梯度遞減法是一種短視的方法，好比遊客在下山的時候遇到非常濃的大霧，只能看見腳下一小塊的地方，遊客就把一個傾角計放在地上，看哪個方向最陡，然後朝著最陡的方向往下滑一段距離，下滑的距離通常根據遊客對當前地形的審視度勢來決定，停下來，再審視周邊哪個方向現在是最陡的。繼續重複上面的傾角計算並往下滑的動作，這跟優化中常用的最陡下降法很類似，可以看做最陡下降法的一個特例。在最陡下降法中，引數的更新使用如下公式：

　　但是在使用梯度遞減法求解神經網路模型時，通常使用的是隨機梯度遞減法（Stochastic Gradient Descent），其公式如下：

　　這個演算法有如下幾點變化：

首先，在計算時不是通覽所有的資料後再執行優化計算，而是對於每個觀測值或

者每組觀測值執行梯度遞減的優化計算。原來的那種演算法因此被叫作批量（Batch）

或者離線（Offline）演算法，而現在這種演算法則被稱為遞增（Incremental）或者

線上（Online）演算法，因為引數估計值隨著觀測組的更新而更新。

其次，這個步進值通常從一開始就固定為一個較小的值。

最後，通過上述公式可以看出，引數更新部分不僅取決於一階偏微分的大小，還

包含了一個動量項這個動量項的效果是將過去的累計更新項的一部分加入到當前參

數的更新項中，即把過去每一步的更新做一個指數遞減的加權求和，可以看作對過

往的更新值的記憶，越遠的記憶影響越小，越近的記憶影響越大。這有助於演算法的

穩定性。如果步進值極小，而動量項裡的控制變數α接近於數值1，那麼線上演算法就

近似於離線演算法。

　　下圖對梯度遞減演算法進行了形象的展示：

　　雖然現在最常見的演算法是基於一階偏微分的梯度遞減法，但是跟其他幾種以前常用的基於二階偏微分的優化演算法進行比較還是比較有趣的，有助於讀者更好地理解這些演算法。
　　基於二階偏微分的演算法通常統稱為牛頓法，因為使用了比一階偏微分更多的資訊，可以看作遊客在下山的過程中霧小了點，能直接看到周邊的地勢。假定整座山是一個平滑的凸形狀，遊客就可以一路下滑到谷底，不用中途停下來。當然，這個谷底也不能保證是最低的，有可能也是某個半山腰的窪地，因為還是有霧，遊客無法徹底看清整個地勢。
　　對一般的牛頓法的一種改進叫作增穩牛頓法（Stabilized Newton Method）。這種方法相當於遊客帶了一個高度計，因此他在滑下去以後可以檢視結果，如果發現地勢反而增高了，那麼遊客退回到原來的地方，重新跳一小步，從而保證每次下滑都能到達更低的點。對這種方法的進一步改進叫作嶺增穩牛頓法（Ridge Stabilized NewtonMethod）。這種方法在上一種方法的基礎上，遊客不僅可以退回到原來的地方，而且重新下滑時還可以選擇跳的方向，以保證有更多的機會使得下滑都離谷底更進一步。

　　對於深度學習模型中的函式，我們看到在每一層的節點都是一個啟用函式套著一個組合函式的形式（參見圖3.5），即常見的複合函式形式，那麼在引數更新部分就需要用到微積分裡面的鏈式法則（Chain Rule）來計算複合函式的導數

　　如果假設損失函式使用均方差，同時採用logistic的sigmoid啟用函式，而組合函式是求和函式，則採用鏈式法則求解引數的更新可以寫作：

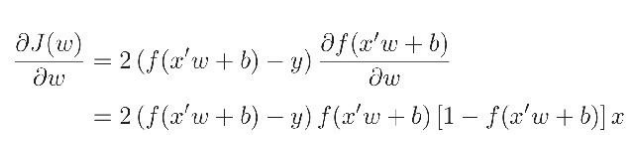
　　將上述公式帶入前面提到的梯度遞減演算法的引數更新步驟中，就可以得到新的引數估計。更新偏置項b採用幾乎一樣的公式，只是這個時候x=1，因此上面公式中最後的x就消掉了。

3：後向傳播演算法

　　上一節對梯度遞減演算法進行了介紹，如果這個神經網路只有一層，那麼反覆運用這個演算法到損失函式，依照上面公式更新引數直到收斂就好了。如果神經網路模型是一個深度模型，在輸入層和輸出層之間包含很多隱含層的話，就需要一個高效率的演算法來儘量減少計算量。後向傳播演算法（Backpropagation）就是一種為了快速估計深度神經網路中的權重值而設計的演算法。

　　設定f0，···，fN代表1，···，N層的決策函式，其中0對應於輸入層，而N對應於輸出層。如果已知各層的權重值和偏置項估計值，那麼可以採用下面的遞迴演算法快速求得在當前引數值下的損失函式大小：

　　為了更新引數值，即權重值和偏置項的估值，後向傳播演算法先正向計算組合函式和其他相關數值，再反向從輸出層N求解損失函式開始，按照梯度遞減演算法逐次往輸入層回算引數的更新量。

　　在深度學習模型所需的計算中會大量使用鏈式法則，這就會使很多計算結果得到重複使用，後向傳播演算法將這些中間結果儲存下來可以極大地減少計算量，提高模型擬合速度。因為在每一層都使用同樣的函式：f：R→R，在這些層中，有：f（1）=f（w），f（2）=f（f（1）），f（3）=f（f（2）），其中上標代表對應的網路層，要計算可以通過鏈式法則得到：

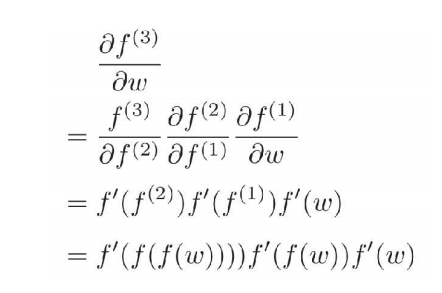
　　可以看到，只需計算f（w）一次，儲存在變數f（1）中，就可以在以後的計算中使用多次，層數越多，效果越明顯。相反，如果不是反向求解引數更新量，而是在正向傳播那一步求解引數更新量，那麼每一步中的f（w）都要重新求解，計算量大增。可以說，後向傳播演算法是神經網路模型普及的基礎之一。

實戰手寫數字識別

　　MNIST手寫數字識別專案因為資料量小，識別任務簡單而成為影象識別入門的第一課，MNIST手寫數字識別專案有如下特點：

　　（1）識別難度低，即使把圖片展開為一維資料，且只使用全連線層也能獲得超過98%的識別準確度。

　　（2）計算量小，不需要GPU加速也可以快速訓練完成。

　　（3）資料容易得到，教程容易得到。

1.1 匯入相關包

import torch

# torchvision包的主要功能是實現資料的處理，匯入和預覽等

import torchvision

from torchvision import datasets

from torchvision import transforms

from torch.autograd import Variable

　　首先，匯入必要的包。對這個手寫數字識別問題的解決只用到了torchvision中的部分功能，所以這裡通過 from torchvision import方法匯入其中的兩個子包 datasets和transforms，我們將會用到這兩個包。

1.2 獲取手寫數字的訓練集和測試集

　　我們就要想辦法獲取手寫數字的訓練集和測試集。使用torchvision.datasets可以輕易實現對這些資料集的訓練集和測試集的下
載，只需要使用 torchvision.datasets再加上需要下載的資料集的名稱就可以了，比如在這個問題中我們要用到手寫數字資料集，它的名稱是MNIST，那麼實現下載的程式碼就是torchvision.datasets.MNIST。其他常用的資料集如COCO、ImageNet、CIFCAR等都可以通過這個方法快速下載和載入。實現資料集下載的程式碼如下：

# 首先獲取手寫數字的訓練集和測試集

# root 用於指定資料集在下載之後的存放路徑

# transform 用於指定匯入資料集需要對資料進行那種變化操作

# train是指定在資料集下載完成後需要載入那部分資料，

# 如果設定為True 則說明載入的是該資料集的訓練集部分

# 如果設定為FALSE 則說明載入的是該資料集的測試集部分

data_train = datasets.MNIST(root="./data/",

transform = transform,

train = True,

download = True)

data_test = datasets.MNIST(root="./data/",

transform = transform,

train = False)

　　其中，root用於指定資料集在下載之後的存放路徑，這裡存放在根目錄下的data資料夾中；transform用於指定匯入資料集時需要對資料進行哪種變換操作，在後面會介紹詳細的變換操作型別，注意，要提前定義這些變換操作；train用於指定在資料集下載完成後需要載入哪部分資料，如果設定為True，則說明載入的是該資料集的訓練集部分；如果設定為False，則說明載入的是該資料集的測試集部分。

1.3 資料預覽和資料裝載

　　在資料下載完成後並且載入後，我們還需要對資料進行裝載。我們可以將資料的載入理解為對圖片的處理，在處理完成後，我們就需要將這些圖片打包好送給我們的模型進行訓練了，而裝載就是這個打包的過程。在裝載時通過batch_size的值來確認每個包的大小，通過shuffle的值來確認是否在裝載的過程中打亂圖片的順序。裝載的程式碼如下：

#資料預覽和資料裝載

# 下面對資料進行裝載，我們可以將資料的載入理解為對圖片的處理，

# 在處理完成後，我們就需要將這些圖片打包好送給我們的模型進行訓練了而裝載就是這個打包的過程

# dataset 引數用於指定我們載入的資料集名稱

# batch_size引數設定了每個包中的圖片資料個數

# 在裝載的過程會將資料隨機打亂順序並進打包

data_loader_train = torch.utils.data.DataLoader(dataset =data_train,

batch_size = 64,

shuffle = True)

data_loader_test = torch.utils.data.DataLoader(dataset =data_test,

batch_size = 64,

shuffle = True)

　　對資料的裝載使用的是是torch.utils.data.DataLoader類，類中的dataset引數用於指定我們載入的資料集名稱，batch_size引數設定了每個包中的圖片資料個數，程式碼中的值是64，所以在每個包中會包含64張圖片。將shuffle引數設定為True，在裝載的過程會將資料隨機打亂順序並進行打包。
　　在裝載完成後，我們可以選取其中一個批次的資料進行預覽，進行資料預覽的程式碼如下：

# 在裝載完成後，我們可以選取其中一個批次的資料進行預覽

images,labels=next(iter(data_loader_train))

img = torchvision.utils.make_grid(images)

img = img.numpy().transpose(1,2,0)

std = [0.5,0.5,0.5]

mean = [0.5,0.5,0.5]

img = img*std +mean

print(labels)

# print([labels[i] for i in range(64)])

# 由於matplotlab中的展示圖片無法顯示，所以現在使用OpenCV中顯示圖片

# plt.imshow(img)

cv2.imshow('win',img)

key_pressed=cv2.waitKey(0)

　　在以上程式碼中使用了iter和next來獲取取一個批次的圖片資料和其對應的圖片標籤，然後使用torchvision.utils中的make_grid類方法將一個批次的圖片構造成網格模式。需要傳遞給torchvision.utils.make_grid的引數就是一個批次的裝載資料，每個批次的裝載資料都是4維的，維度的構成從前往後分別為batch_size、channel、height和weight，分別對應一個批次中的資料個數、每張圖片的色彩通道數、每張圖片的高度和寬度。在通過torchvision.utils.make_grid之後，圖片的維度變成了（channel,height,weight），這個批次的圖片全部被整合到了一起，所以在這個維度中對應的值也和之前不一樣了，但是色彩通道數保持不變。

　　若我們想使用Matplotlib將資料顯示成正常的圖片形式，則使用的資料首先必須是陣列，其次這個陣列的維度必須是
（height,weight,channel），即色彩通道數在最後面。所以我們要通過numpy和transpose完成原始資料型別的轉換和資料維度的交換，這樣才能夠使用Matplotlib繪製出正確的影象。

　　在完成資料預覽的程式碼中，我們先列印輸出了這個批次中的資料的全部標籤，然後才對這個批次中的所有圖片資料進行顯示，程式碼如下

tensor([7, 1, 8, 3, 2, 3, 6, 7, 3, 9, 7, 3, 0, 0, 7, 5, 0, 0, 2, 5, 4, 4, 2, 7,

6, 9, 8, 1, 8, 3, 7, 1, 8, 9, 6, 5, 3, 2, 0, 0, 4, 6, 1, 9, 2, 2, 2, 6,

9, 8, 7, 2, 2, 6, 8, 2, 5, 8, 6, 1, 9, 9, 9, 8])

　　效果如下，可以看到輸出的首先是64張圖片對應的標籤，然後是64張圖片的預覽結果：

1.4 模型搭建和引數優化　

　　在順利完成資料裝載後，我們就可以開始編寫卷積神經網路模型的搭建和引數優化的程式碼了，因為我們想要搭建一個包含了卷積層，啟用函式，池化層，全連線層的卷積神經網路來解決這個問題，所以模型在結構上會和之前簡單的神經網路有所區別，當然，各個部分的功能實現依然是通過torch.nn中的類來完成的，比如卷積層使用torch.nn.Conv2d類方法來搭建，啟用層使用torch.nn.ReLU類來搭建；池化層使用torch.nn.MaxPool2d類方法來搭建；全連線層使用torch.nn.Linear類方法來搭建。

卷積神經網路CNN的結構一般包含這幾層：

輸入層：用於資料的輸入

卷積層：使用卷積核進行特徵提取和特徵對映

激勵層：由於卷積也是一種線性運算，因此需要增加非線性對映

池化層：進行下采樣，對特徵圖稀疏處理，減少特徵資訊的損失

輸出層：用於輸出結果

　　實現卷積神經網路模型搭建的程式碼如下：

#模型搭建和引數優化

# 在順利完成資料裝載後，我們可以開始編寫卷積神經網路模型的搭建和引數優化的程式碼

#卷積層使用torch.nn.Conv2d類來搭建

# 啟用層使用torch.nn.ReLU 類方法來搭建

# 池化層使用torch.nn.MaxPool2d類方法來搭建

# 全連線層使用 torch.nn.Linear 類方法來搭建

class Model(torch.nn.Module):

def __init__(self):

super(Model,self).__init__()

self.conv1 = torch.nn.Sequential(

torch.nn.Conv2d(1,64,kernel_size=3,stride=1,padding=1),

torch.nn.ReLU(),

torch.nn.Conv2d(64,128,kernel_size=3,stride=1,padding=1),

torch.nn.ReLU(),

torch.nn.MaxPool2d(stride=2,kernel_size=2))

self.dense = torch.nn.Sequential(

torch.nn.Linear(14*14*128,1024),

torch.nn.ReLU(),

torch.nn.Dropout(p = 0.5),

torch.nn.Linear(1024,10)

)

def forward(self, x):

x = self.conv1(x)

x = x.view(-1,14*14*128)

x = self.dense(x)

return x

　　因為這個問題並不複雜，所以我們選擇搭建一個在結構層次上有所簡化的卷積神經網路模型，在結構上使用了兩個卷積層：一個最大池化層和兩個全連線層。

　　最後說一下程式碼中前向傳播forward函式中的內容，首先經過self.conv1進行卷積處理，然後進行x.view(-1,14*14*128)，對引數實現扁平化，因為之後緊接著的就是全連線層，所以如果不進行扁平化，則全連線層的實際輸出的引數維度和其定義輸入的維度將不匹配，程式將會報錯，最後通過self.dense定義的全連線層進行最後的分類。

　　在編寫完搭建卷積神經網路模型的程式碼後，我們就可以開始對模型進行訓練和對引數進行優化了。首先，定義在訓練之前使用哪種損失函式和優化函式：

# 在編寫完搭建卷積神經網路模型的程式碼後，我們可以對模型進行訓練和引數進行優化了

# 首先定義在訓練之前使用哪種損失函式和優化函式

# 下面定義了計算損失值的損失函式使用的是交叉熵

# 優化函式使用的額是Adam自適應優化演算法

model = Model()

cost = torch.nn.CrossEntropyLoss()

optimizer = torch.optim.Adam(model.parameters())

　　在以上的程式碼中定義了計算損失值的損失函式使用的是交叉熵，也確定了優化函式使用的是Adam自適應優化演算法，需要優化的引數在Model中生成的全部引數，因為沒有定義學習效率的值，所以使用預設值，然後通過列印輸出的方式檢視搭建好的模型的完整結構們只需要print(model)就OK。輸出的結果如下：

Model(

(conv1): Sequential(

(0): Conv2d(1, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))

(1): ReLU()

(2): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))

(3): ReLU()

(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)

)

(dense): Sequential(

(0): Linear(in_features=25088, out_features=1024, bias=True)

(1): ReLU()

(2): Dropout(p=0.5)

(3): Linear(in_features=1024, out_features=10, bias=True)

)

　　最後，卷積神經網路模型進行模型訓練和引數優化的程式碼如下：

# 卷積神經網路模型進行模型訓練和引數優化的程式碼

n_epochs = 5

for epoch in range(n_epochs):

running_loss = 0.0

running_corrrect = 0

print("Epoch {}/{}".format(epoch, n_epochs))

print("-"*10)

for data in data_loader_train:

X_train , y_train = data

X_train,y_train = Variable(X_train),Variable(y_train)

outputs = model(X_train)

_,pred = torch.max(outputs.data,1)

optimizer.zero_grad()

loss = cost(outputs,y_train)

loss.backward()

optimizer.step()

running_loss += loss.data[0]

running_corrrect += torch.sum(pred == y_train.data)

testing_correct = 0

for data in data_loader_train:

X_test,y_test = data

X_test,y_test = Variable(X_test),Variable(y_test)

outputs = model(X_test)

_,pred = torch.max(X_test)

testing_correct += torch.sum(pred == y_test.data)

print("Loss is {:.4f}, Train Accuracy is:{:.4f}%,Test Accuracy is:{:.4f}"

.format(running_loss/len(data_train),100*running_corrrect/len(data_train),

100*testing_correct/len(data_test)))

　　總的訓練次數為5次，訓練中的大部分程式碼和之前的相比較沒有大的改動，增加的內容都在原來的基礎上加入了更多的列印輸出，其目的是更好的顯示模型訓練過程中的細節，同時，在每輪訓練完成後，會使用測試集驗證模型的泛化能力並計算準確率。在模型訓練過程中列印輸出的結果如下：

（未實現原文結果！！！）

Epoch 0/5

----------

Process finished with exit code -1073741795 (0xC000001D)

（這是原文作者實現的結果）

　　可以看到，結果表現的非常不錯，訓練集達到的最高準確率為99.73%，而測試集達到的最高準確率為98.96%，如果我們使用功能更強大的卷積神經網路模型，則會取得比現在更好的結果。為了驗證我們訓練的模型是不是真的已如結果顯示的一樣準確，則最好的方法就是隨機選取一部分測試集中的圖片，用訓練好的模型進行預測，看看和真實值有多大的偏差，並對結果進行視覺化。

　　本人對程式碼進行修改，實現的結果如下（windows7實現）：

1

Epoch [1/5], Iter [100/600] Loss: 0.1948

Epoch [1/5], Iter [200/600] Loss: 0.1884

Epoch [1/5], Iter [300/600] Loss: 0.1267

Epoch [1/5], Iter [400/600] Loss: 0.2222

Epoch [1/5], Iter [500/600] Loss: 0.0289

Epoch [1/5], Iter [600/600] Loss: 0.0657

Epoch [2/5], Iter [100/600] Loss: 0.0138

Epoch [2/5], Iter [200/600] Loss: 0.1130

Epoch [2/5], Iter [300/600] Loss: 0.0487

Epoch [2/5], Iter [400/600] Loss: 0.0206

Epoch [2/5], Iter [500/600] Loss: 0.0284

Epoch [2/5], Iter [600/600] Loss: 0.0299

Epoch [3/5], Iter [100/600] Loss: 0.0279

Epoch [3/5], Iter [200/600] Loss: 0.0766

Epoch [3/5], Iter [300/600] Loss: 0.0158

Epoch [3/5], Iter [400/600] Loss: 0.0143

Epoch [3/5], Iter [500/600] Loss: 0.0180

Epoch [3/5], Iter [600/600] Loss: 0.0042

Epoch [4/5], Iter [100/600] Loss: 0.0117

Epoch [4/5], Iter [200/600] Loss: 0.0151

Epoch [4/5], Iter [300/600] Loss: 0.0034

Epoch [4/5], Iter [400/600] Loss: 0.0144

Epoch [4/5], Iter [500/600] Loss: 0.0482

Epoch [4/5], Iter [600/600] Loss: 0.0550

Epoch [5/5], Iter [100/600] Loss: 0.0393

Epoch [5/5], Iter [200/600] Loss: 0.0028

Epoch [5/5], Iter [300/600] Loss: 0.0368

Epoch [5/5], Iter [400/600] Loss: 0.0250

Epoch [5/5], Iter [500/600] Loss: 0.1075

Epoch [5/5], Iter [600/600] Loss: 0.0663

Process finished with exit code 0

1.5 完整程式碼及解析

（原文程式碼，本人未實現）

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

#_*_coding:utf-8_*_

import matplotlib.pyplot as plt

import numpy as np

import cv2

import time

import torch

# torchvision包的主要功能是實現資料的處理，匯入和預覽等

import torchvision

from torchvision import datasets

from torchvision import transforms

from torch.autograd import Variable

start_time = time.time()

# 對資料進行載入及有相應變換,將Compose看成一種容器，他能對多種資料變換進行組合

# 傳入的引數是一個列表，列表中的元素就是對載入的資料進行的各種變換操作

transform = transforms.Compose([transforms.ToTensor(),

transforms.Normalize(mean=[0.5,0.5,0.5],std=[0.5,0.5,0.5])])

# 首先獲取手寫數字的訓練集和測試集

# root 用於指定資料集在下載之後的存放路徑

# transform 用於指定匯入資料集需要對資料進行那種變化操作

# train是指定在資料集下載完成後需要載入那部分資料，

# 如果設定為True 則說明載入的是該資料集的訓練集部分

# 如果設定為FALSE 則說明載入的是該資料集的測試集部分

data_train = datasets.MNIST(root="./data/",

transform = transform,

train = True,

download = True)

data_test = datasets.MNIST(root="./data/",

transform = transform,

train = False)

#資料預覽和資料裝載

# 下面對資料進行裝載，我們可以將資料的載入理解為對圖片的處理，

# 在處理完成後，我們就需要將這些圖片打包好送給我們的模型進行訓練了而裝載就是這個打包的過程

# dataset 引數用於指定我們載入的資料集名稱

# batch_size引數設定了每個包中的圖片資料個數

# 在裝載的過程會將資料隨機打亂順序並進打包

data_loader_train = torch.utils.data.DataLoader(dataset =data_train,

batch_size = 64,

shuffle = True)

data_loader_test = torch.utils.data.DataLoader(dataset =data_test,

batch_size = 64,

shuffle = True)

# 在裝載完成後，我們可以選取其中一個批次的資料進行預覽

images,labels = next(iter(data_loader_train))

img = torchvision.utils.make_grid(images)

img = img.numpy().transpose(1,2,0)

std = [0.5,0.5,0.5]

mean = [0.5,0.5,0.5]

img = img*std +mean

# print(labels)

print([labels[i] for i in range(64)])

# 由於matplotlab中的展示圖片無法顯示，所以現在使用OpenCV中顯示圖片

# plt.imshow(img)

# cv2.imshow('win',img)

# key_pressed=cv2.waitKey(0)

#模型搭建和引數優化

# 在順利完成資料裝載後，我們可以開始編寫卷積神經網路模型的搭建和引數優化的程式碼

#卷積層使用torch.nn.Conv2d類來搭建

# 啟用層使用torch.nn.ReLU 類方法來搭建

# 池化層使用torch.nn.MaxPool2d類方法來搭建

# 全連線層使用 torch.nn.Linear 類方法來搭建

class Model(torch.nn.Module):

def __init__(self):

super(Model,self).__init__()

self.conv1 = torch.nn.Sequential(

torch.nn.Conv2d(1,64,kernel_size=3,stride=1,padding=1),

torch.nn.ReLU(),

torch.nn.Conv2d(64,128,kernel_size=3,stride=1,padding=1),

torch.nn.ReLU(),

torch.nn.MaxPool2d(stride=2,kernel_size=2))

self.dense = torch.nn.Sequential(

torch.nn.Linear(14*14*128,1024),

torch.nn.ReLU(),

torch.nn.Dropout(p = 0.5),

torch.nn.Linear(1024,10)

)

# 我們通過繼承torch.nn.Modeule來構造網路，因為手寫數字

# 識別比較簡單，我們只是用了兩個卷積層，一個最大池化層，兩個全連線層。

# 在向前傳播過程中進行x.view(-1, 14 * 14 * 128)

# 對引數實現扁平化。最後通過自己self.dense定義的全連線層進行最後的分類

def forward(self, x):

x = self.conv1(x)

x = x.view(-1,14*14*128)

x = self.dense(x)

return x

# 在編寫完搭建卷積神經網路模型的程式碼後，我們可以對模型進行訓練和引數進行優化了

# 首先定義在訓練之前使用哪種損失函式和優化函式

# 下面定義了計算損失值的損失函式使用的是交叉熵

# 優化函式使用的額是Adam自適應優化演算法

model = Model()

# 將所有的模型引數移動到GPU上

if torch.cuda.is_available():

model.cuda()

cost = torch.nn.CrossEntropyLoss()

optimizer = torch.optim.Adam(model.parameters())

# print(model)

# 卷積神經網路模型進行模型訓練和引數優化的程式碼

n_epochs = 5

for epoch in range(n_epochs):

running_loss = 0.0

running_correct = 0

print("Epoch {}/{}".format(epoch, n_epochs))

print("-"*10)

for data in data_loader_train:

X_train , y_train = data

# 有GPU加下面這行，沒有不用加

# X_train, y_train = X_train.cuda(), y_train.cuda()

X_train , y_train = Variable(X_train),Variable(y_train)

# print(y_train)

outputs = model(X_train)

# print(outputs)

_,pred = torch.max(outputs.data,1)

optimizer.zero_grad()

loss = cost(outputs,y_train)

loss.backward()

optimizer.step()

# running_loss += loss.data[0]

running_loss += loss.item()

running_correct += torch.sum(pred == y_train.data)

# print("ok")

# print("**************%s"%running_corrrect)

print("train ok ")

testing_correct = 0

for data in data_loader_test:

X_test,y_test = data

# 有GPU加下面這行，沒有不用加

# X_test, y_test = X_test.cuda(), y_test.cuda()

X_test,y_test = Variable(X_test),Variable(y_test)

outputs = model(X_test)

_, pred = torch.max(outputs,1)

testing_correct += torch.sum(pred == y_test.data)

# print(testing_correct)

print( "Loss is :{:.4f},Train Accuracy is:{:.4f}%,Test Accuracy is:{:.4f}".format(

running_loss / len(data_train),100 * running_correct / len(data_train),

100 * testing_correct / len(data_test)))

stop_time = time.time()

print("time is %s" %(stop_time-start_time))

（本人對原文程式碼進行修改，然後實現的是這個程式碼）

import torch

import torch.nn as nn

import torchvision.datasets as normal_datasets

import torchvision.transforms as transforms

from torch.autograd import Variable

num_epochs = 5

batch_size = 100

learning_rate = 0.001

# 將資料處理成Variable, 如果有GPU, 可以轉成cuda形式

def get_variable(x):

x = Variable(x)

return x.cuda() if torch.cuda.is_available() else x

# 從torchvision.datasets中載入一些常用資料集

train_dataset = normal_datasets.MNIST(

root='./mnist/', # 資料集儲存路徑

train=True, # 是否作為訓練集

transform=transforms.ToTensor(), # 資料如何處理, 可以自己自定義

download=True) # 路徑下沒有的話, 可以下載

# 見資料載入器和batch

test_dataset = normal_datasets.MNIST(root='./mnist/',

train=False,

transform=transforms.ToTensor())

train_loader = torch.utils.data.DataLoader(dataset=train_dataset,

batch_size=batch_size,

shuffle=True)

test_loader = torch.utils.data.DataLoader(dataset=test_dataset,

batch_size=batch_size,

shuffle=False)

# 兩層卷積

class CNN(nn.Module):

def __init__(self):

super(CNN, self).__init__()

# 使用序列工具快速構建

self.conv1 = nn.Sequential(

nn.Conv2d(1, 16, kernel_size=5, padding=2),

nn.BatchNorm2d(16),

nn.ReLU(),

nn.MaxPool2d(2))

self.conv2 = nn.Sequential(

nn.Conv2d(16, 32, kernel_size=5, padding=2),

nn.BatchNorm2d(32),

nn.ReLU(),

nn.MaxPool2d(2))

self.fc = nn.Linear(7 * 7 * 32, 10)

def forward(self, x):

out = self.conv1(x)

out = self.conv2(out)

out = out.view(out.size(0), -1) # reshape

out = self.fc(out)

return out

cnn = CNN()

if torch.cuda.is_available():

cnn = cnn.cuda()

# 選擇損失函式和優化方法

loss_func = nn.CrossEntropyLoss()

optimizer = torch.optim.Adam(cnn.parameters(), lr=learning_rate)

for epoch in range(num_epochs):

for i, (images, labels) in enumerate(train_loader):

images = get_variable(images)

labels = get_variable(labels)

outputs = cnn(images)

loss = loss_func(outputs, labels)

optimizer.zero_grad()

loss.backward()

o


              
           
              
              
            
            相關推薦
			   
            
            
            
 

    

    
    機器學習--k-近鄰演算法（kNN）實現手寫數字識別
      
								
								            
						
                這裡的手寫數字以0,1的形式儲存在文字檔案中，大小是32x32.目錄trainingDigits有1934個樣本。0-9每個數字大約有200個樣本，命名規則如下：



下劃線前的數字代表是樣本0-9的 

  
 

    

    
    pytorch 入門（二） cnn 手寫數字識別
      
							
							
							import torch
import torch.nn as nn
import torchvision.datasets as normal_datasets
import torchvision.transforms as transforms
from  

  
 

    

    
    Tensorflow深度學習筆記（二）--BPNN手寫數字識別視覺化
      
							
							
							資料集：MNIST  
啟用函式：Relu  
損失函式：交叉熵  
Optimizer：AdamOptimizer  
視覺化工具：tensorboad



迭代21epoch，accuracy結果如下： 
Iter 16,Testing Accuracy: 

  
 

    

    
    Pytorch 快速入門（六）MNIST 手寫數字識別之CNN
      
                接觸過深度學習的朋友對MNIST資料集肯定不陌生。基本上算是玩神經網路裡的“hello,world！”本節基於MNIST資料集，實現CNN學習過程。下面是一個 CNN 最後一層的學習過程, 我們先視覺化看看:MNIST手寫資料 首先是資料集下載，為了看看資料集裡究竟是長什麼樣 

  
 

    

    
    【深度學習】python實現簡單神經網路以及手寫數字識別案例
       
 
  
  
 前言 
 
     
      
       
        
       
       
        \quad
       
      
     
     
      
       
        
       
       
        \qu 

  
 

    

    
    TensorFlow程式碼實現（一）[MNIST手寫數字識別]
      
							
							
							最簡單的神經網路結構：


資料來源準備：資料在之前的文章中分析過了
在這裡我們就構造一層神經網路： 
前提準備： 
引數： 
train images：因為圖片是28*28的個數，換算成一維陣列就是784，因此我們定義x = tf.placeholder(tf 

  
 

    

    
    基於k近鄰（KNN）的手寫數字識別
      
                
作者：faaronzheng 轉載請註明出處！
最近再看Machine
 Learning in Action. k近鄰演算法這一章節提供了不少例子，本著Talk is cheap的原則，我們用手寫數字識別來實際測試一下。 簡單的介紹一下k近鄰演算法（KNN）：給定測試樣本 

  
 

    

    
    深度學習之PyTorch實戰（3）——實戰手寫數字識別
       
 
 　　上一節，我們已經學會了基於PyTorch深度學習框架高效，快捷的搭建一個神經網路，並對模型進行訓練和對引數進行優化的方法，接下來讓我們牛刀小試，基於PyTorch框架使用神經網路來解決一個關於手寫數字識別的計算機視覺問題，評價我們搭建的模型的標準是它是否能準確的對手寫數字圖片進行識別。 
 　　 

  
 

    

    
    20180813視頻筆記 深度學習基礎上篇（1）之必備基礎知識點 深度學習基礎上篇（2）神經網絡模型視頻筆記：深度學習基礎上篇（3）神經網絡案例實戰     和    深度學習基礎下篇
      計算   概念   人臉識別   大量   png   技巧   表現   lex   github   深度學習基礎上篇（3）神經網絡案例實戰
https://www.bilibili.com/video/av27935126/?p=1
第一課:開發環境的配置
Anaconda的安裝 
庫的安裝
Windo 

  
 

    

    
    深度學習實戰（3）-打造自己的影象識別模型
      
                這個筆記弄的我難受，推薦觀看者還是看原書吧............ 

用VGG16作為例子

簡單介紹：如何使用，去掉尾部，保留引數初始值





如何訓練



資料準備



檔案轉換



data_convert.py原始碼：

# coding:utf-8
fr 

  
 

    

    
    Linux學習之路--Mariadb（3）基本使用操作【20】---20180123
      result   run   page   提高   進行   組成   varchar   alias   pan   一、MariaDB程序1、MariaDB的程序組成Client     mysql：CLI交互式客戶端程序    mysqldump,mysqladmin...Server    mysq 

  
 

    

    
    MySQL學習之路4（3）
       
  
  
 資料庫的基本操作3 
 4.刪除資料表 4.1刪除沒有被關聯的表 DROP TABLE可以一次刪除一個或多個沒有被其他表關聯的的資料表。語法格式如下： DROP TABLE [IF EXISITS] 表1，表2，……，表n； 如果要刪除的資料表不存在，則會出現一條錯誤資訊： ERROR 10 

  
 

    

    
    深度學習之物體檢測（一）R-CNN
      
                作者Rgb

在這之前大部分物體檢測演算法都是基於傳統的影象處理方法，這是第一篇將深度學習用到物體檢測上的文章，直接影響是2012年ALEXNET在比賽中的重大成功。

簡單來說，RCNN使用以下四步實現目標檢測：

a. 在影象中用slective search 方法 確定 

  
 

    

    
    深度學習之路：（一）Keras中mnist資料集測試
       
 
  
  
 Keras環境搭建 
  
  本地環境 MacOS 
  
 一、安裝Anaconda 
 1、下載Anaconda最新版本：官網下載地址 
  
  
  附：清華映象源   
  
 2、下載後直接安裝，點選next 
 3、檢測版本 
  
  開啟終端 
  輸入conda - 

  
 

    

    
    深度學習之風格遷移（三）——Deep Photo Style Transfer(Fujun Luan)
      
							
							
							前面已經介紹瞭如何利用神經網路進行風格遷移，參見部落格深度學習之風格遷移（一）——Neural Style(Gatys) 。該文介紹了怎麼把藝術作品的風格遷移到真實圖片中去，生成的圖片是帶有藝術色彩的繪畫作品。那麼現在給定兩個真實的圖片，一張作為風格圖片，一張作 

  
 

    

    
    深度學習之softmax函式（一）
      
                       本文關於深度學習的softmax函式做了詳細的介紹，並給出深度學習中損失函式的對比連結。

一、Softmax詳解













二、Logistic函式

Logistic函式又稱邏輯斯諦函式，也就是經常說的sigmoid函式，它的幾何形狀也就是一 

  
 

    

    
    STL學習之map容器（3）
      
                
map::find

iterator find ( const key_type& x );
const iterator find( const key_type& x) const;
獲取元素的迭代器

獲取map容器中指定鍵值x的元素，如果找到，返回 

  
 

    

    
    fastai案例學習（3）——MNIST手寫資料集
       
 
 
 本文主要介紹fastai自帶的案例，MNIST手寫資料集。 
 1、匯入包。 
 import fastai
from fastai import *
from fastai.vision import * 
 2、下載MNIST資料集。 
 path = untar_data(URLs.MNI 

  
 

    

    
    Deeplearning4j 實戰（2）：Deeplearning4j 手寫體數字識別Spark實現
       
 
 在前兩天的部落格中，我們用Deeplearning4j做了Mnist資料集的分類。算是第一個深度學習的應用。像Mnist資料集這樣圖片尺寸不大，而且是黑白的開源圖片集在本地完成訓練是可以的，畢竟我們用了Lenet這樣相對簡單的網路結構，而且本地的機器配置也有8G左右的記憶體。但實際生產中，圖片的數量 

  
 

    

    
    各種機器學習方法（線性迴歸、支援向量機、決策樹、樸素貝葉斯、KNN演算法、邏輯迴歸）實現手寫數字識別並用準確率、召回率、F1進行評估
      
                
本文轉自：http://blog.csdn.net/net_wolf_007/article/details/51794254



前面兩章對資料進行了簡單的特徵提取及線性迴歸分析。識別率已經達到了85%， 完成了數字識別的第一步：資料探測。
這一章要做的就各


        
      
    
    
  
    搜尋
    
        
      
      
    
  
 
  
  
    基礎教學
     
    Mysql入門  
     Sql入門 
      Android入門 
       Docker入門 
        Go語言入門 
         Ruby程式入門 
          Python入門 
           Python進階 
            Django入門 
             Python爬蟲入門 
             
      
      
  
   
  
    最近訪問
    
  	      
  
      
    
  

 

 


  
    
      
        
          首頁
前端設計
程式設計
免費資源
實用技巧
資料庫
資訊
字典
        
          Copyright © 2002-2020  程式人生 796T.COM All rights reserved.