一、前言

二叉樹的遍歷是比較多樣化的遍歷，有很多種遍歷方式，先序遍歷，中序遍歷，後序遍歷，層次遍歷等等。本次給大家講的是層次遍歷，為了方便，我將題目中的資料改為編號，從左往右，從上往下依次遍歷。方便大家看到結果。

二、題目

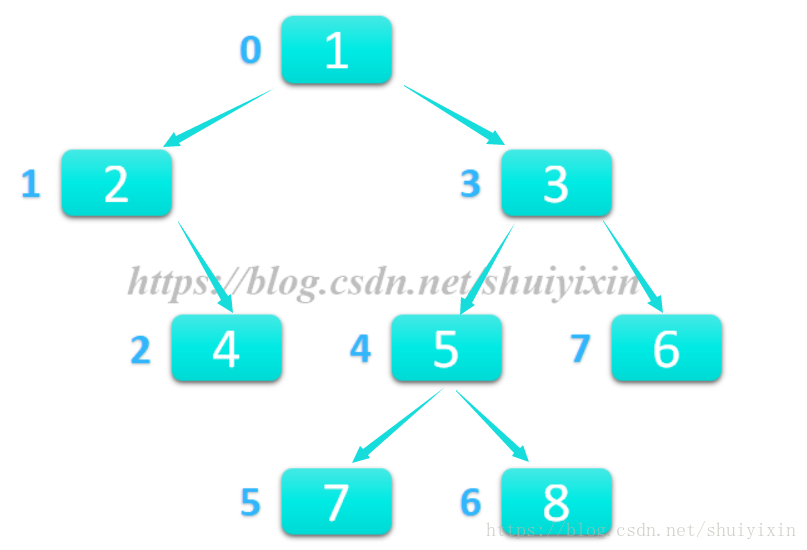
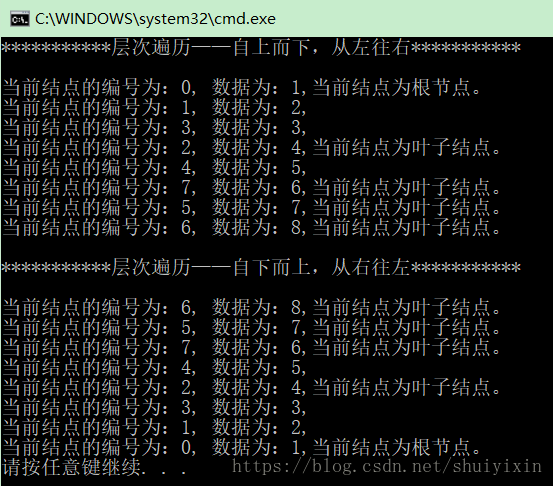
將下圖用二叉樹存入，並通過層次遍歷方式，自上而下，從左往右對該樹進行遍歷。其中圓角矩形內為結點資料，旁邊數字為結點編號，編號為0的結點為根節點，箭頭指向的結點為箭尾的孩子結點。要求遍歷每個結點時能夠查詢當前結點的資料以及編號，如果結點是根節點或者葉子結點，請說明。

實現功能後，將層次遍歷變換為：自下而上，從右往左對該樹進行遍歷。並將結果輸出。

 三、程式碼

#define MAXQUEUESIZE 10

#include<iostream>
#include<malloc.h>

using namespace std;

typedef struct BiTNode {
	int data,number;
	struct BiTNode *lChild, *rChild,*parent;

}BiTNode,*BiTree;

typedef struct {
	BiTree *qBase;
	int front;
	int rear;
}SqQueue;

typedef struct LNode{
	BiTree data;
	struct LNode *next;
}LNode,*LinkStack;

int InitQueue(SqQueue &SQ) {
	SQ.qBase = (BiTree*)malloc(MAXQUEUESIZE * sizeof(SqQueue));
	if (!SQ.qBase)
	{
		cout << "空間分配失敗（Allocate space failure）" << endl;
		exit(OVERFLOW);
	}
	SQ.front = SQ.rear = 0;
	return 1;
}

int EnQueue(SqQueue &SQ, BiTree e) {
	if ((SQ.rear+1)% MAXQUEUESIZE == SQ.front)
	{
		cout << "佇列已滿(The queue is full)" << endl;
		exit(OVERFLOW);
	}
	SQ.qBase[SQ.rear] = e;
	SQ.rear = (SQ.rear + 1) % MAXQUEUESIZE;
	return 1;
}

int DeQueue(SqQueue &SQ, BiTree &e) {
	if (SQ.rear == SQ.front)
	{
		cout << "佇列已空(The queue is null)" << endl;
		return 0;
	}
	e = SQ.qBase[SQ.front];
	SQ.front = (SQ.front + 1) % MAXQUEUESIZE;
	return 1;
}

int InitStack(LinkStack &S) {
	S = (LinkStack)malloc(sizeof(LNode));
	if (!S)
	{
		cout << "空間分配失敗（Allocate space failure）" << endl;
		exit(OVERFLOW);
	}
	S->next = NULL;
	return 1;
}

int Push(LinkStack &S, BiTree e) {
	LinkStack p = (LinkStack)malloc(sizeof(LNode));
	if (!p)
	{
		cout << "結點分配失敗（Allocate node failure）" << endl;
		exit(OVERFLOW);
	}
	S->data = e;
	p->next = S;
	S = p;
	return 1;
}
int Pop(LinkStack &S, BiTree &e) {
	LinkStack p = S->next;
	if (!p)
	{
		cout << "棧空(The stack is null)" << endl;
		exit(OVERFLOW);
	}
	e = p->data;
	S->next = p->next;
	free(p);
	return 1;
}

int number = 0;
int yon = 0;
int yesOrNo[] = { 1,0,1,0,0,1,1,1,0,0,1,0,0,1,0,0 };
int numData[] = { 1,2,4,3,5,7,8,6 };
BiTree treeParent = NULL;

int OperationBiTree(BiTree &BT) {
	BT = (BiTree)malloc(sizeof(BiTNode));
	if (!BT)
	{
		cout << "空間分配失敗" << endl;
		exit(OVERFLOW);
	}
	BT->number = number;
	number++;
	BT->data = numData[BT->number];
	BT->lChild = NULL;
	BT->rChild = NULL;
	BT->parent = treeParent;
	return 1;
}

void PreOrderCreatBiTree(BiTree &BT) {

	OperationBiTree(BT);
	treeParent = BT;
	if (yesOrNo[yon++])
		PreOrderCreatBiTree(BT->lChild);
	treeParent = BT;
	if (yesOrNo[yon++])
		PreOrderCreatBiTree(BT->rChild);
}

void VisitBiTree(BiTree BT) {
	cout << "當前結點的編號為：" << BT->number << ", ";
	cout << "資料為：" << BT->data << ",";
	if (!BT->parent)
		cout << "當前結點為根節點。";
	if (!BT->lChild && !BT->rChild)
		cout << "當前結點為葉子結點。";
	cout << endl;

}

void LevelOrderBiTree(BiTree BT, LinkStack &S) {
	SqQueue SQ;
	InitQueue(SQ);
	InitStack(S);
	BiTree t = BT;
	EnQueue(SQ, t);
	while (SQ.rear != SQ.front)
	{
		DeQueue(SQ, t);
		Push(S, t);
		VisitBiTree(t);
		if (t->lChild)
			EnQueue(SQ, t->lChild);
		if (t->rChild)
			EnQueue(SQ, t->rChild);
	}
}

void main() {
	BiTree BT,t;
	LinkStack S;
	PreOrderCreatBiTree(BT);

	cout << "***********層次遍歷——自上而下，從左往右***********\n\n";
	LevelOrderBiTree(BT,S);

	cout << "\n***********層次遍歷——自下而上，從右往左***********\n\n";
	while (S->next)
	{
		Pop(S, t);
		VisitBiTree(t);
	}
	
}
 

四、實現效果