前言

主席樹可真是個好東西

之前一直都覺得挺難的

今天一看

woc這麼簡單!

怎麼可能,我還是太蒟蒻了

感謝akakw1大佬的指導!

正文:

一.前置知識及演算法思路

1.可持久化

因為主席樹是可持久化線段樹,所以還是有必要了解一下可持久化

可持久化的資料結構是可以支援訪問任一歷史版本的(也就是每一次修改操作之前的情況)

2.如何實現

以可持久化線段樹為例:

很自然的,我們可以想到對於每一個版本開一個線段樹

但考慮到這樣做的空間複雜度是\(O(k*n*4)\) (k為修改次數)

果斷放棄

3.優化

考慮進行優化.

盜一張圖

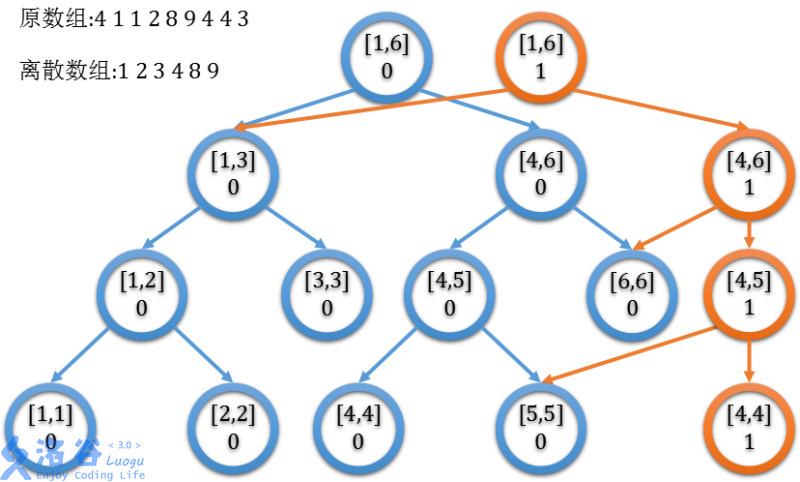
假如我們現在要修改的點是4(也就是區間[4,4])

可以發現區間[1,3]和區間[5,6]是完全沒有改變的,

因此我們考慮利用上一版本

具體解釋:當我們遞迴[1,6]的左子樹[1,3]時發現4根本沒有在其中,這也就意味著當前版本的[1,3]節點與上一版本完全一樣!

因此我們直接讓新開的根節點(也就是橙色的[1.6])的左子節點指向原來的根節點(也就是藍色的[1.6])的左子節點(藍色的[1,3]);

接著繼續遞迴右子樹[4,6],發現[6,6]也可以直接利用上一版本,以此類推

然後就發現每一次就只要開\(log_2 n\)個節點了!

二.例題

洛谷 P3834【模板】可持久化線段樹 1（主席樹）

題目就是讓你查詢區間[l,r]的第k小值

離散化一下值域

這題開個可持久化值域線段樹就可以啦

程式碼

 1 #include<bits/stdc++.h>
 2 #define R register int
 3 #define gc getchar
 4 using namespace std;
 5 const int MAX_N=2e5+10,MAX_MLOGN=4e6+10;
 6 int tot,root[MAX_N],n,m,q,a[MAX_N],b[MAX_N];
 7 int rd()
 8 {
 9     int ans=0,flag=1
 
;
10     char ch=gc();
11     while((ch<'0'||ch>'9')&&ch!='-')ch=gc();
12     if(ch=='-')flag=-1,ch=gc();
13     while(ch>='0'&&ch<='9')ans=ans*10+ch-48,ch=gc();
14     return ans*flag;
15 }
16 struct Segment_Tree{
17     int l,r;
18     int dat;
19 }t[MAX_MLOGN];
20 
21 //l,r為左右子節點編號
22 //dat是當前版本的序列下 x的個數(L_i<=x<=R_i(i為節點編號,這裡的L,R*要與結構體中的l,r加以區分))
23 //*這裡的L,R是指當前節點線上段樹中所代表的值域[L,R]
24 
25 int Build(int l,int r)//l,r都為值域,函式的返回值是節點編號
26 //呼叫入口為Build(1,m) *(1,m)為離散後的值域
27 {
28     int p=++tot;
29     t[p].dat=0;
30     //因為主席樹不再是完全二叉樹,不滿足t[p*2]是t[p]的子節點
31     //所以直接用tot來記錄節點編號
32     if(l>=r)
33     {
34         return p;
35     }
36     int mid=(l+r)>>1;
37     t[p].l=Build(l,mid);
38     t[p].r=Build(mid+1,r);
39     return p;
40 }
41 int Insert(int pre,int l,int r,int x)//pre是上一版本的同一位置的節點的編號;l,r為值域;x為值
42 //函式返回值仍然是節點編號
43 {
44     int p=++tot;
45     t[p].l=t[pre].l,t[p].r=t[pre].r;
46     t[p].dat=t[pre].dat+1;//可以先直接繼承上一版本的資料
47     int mid=(l+r)>>1;
48     if(l<r)
49     {
50         if(x<=mid)//按值域劃分,不用多說
51         {
52             t[p].l=Insert(t[pre].l,l,mid,x);//這裡是遞迴t[pre]而不是t[p]
53         }
54         else
55         {
56             t[p].r=Insert(t[pre].r,mid+1,r,x);//同理
57         }
58     }
59     return p;
60 }
61 int Query(int u,int v,int l,int r,int k)
62 {
63     if(l>=r)return l;
64     int mid=(l+r)>>1;
65     int tmp=t[t[v].l].dat-t[t[u].l].dat;
66     if(tmp<k)return Query(t[u].r,t[v].r,mid+1,r,k-tmp);
67     else return Query(t[u].l,t[v].l,l,mid,k);
68 }
69 int main()
70 {
71     n=rd(),q=rd();
72     for(R i=1;i<=n;i++)
73     {
74         b[i]=a[i]=rd();
75     }
76     /**/
77     sort(b+1, b+1+n);
78     m=unique(b+1,b+1+n)-b-1;//離散化
79     /**/
80     root[0]=Build(1,m);
81     for(R i=1;i<=n;i++)
82     {
83         R t=lower_bound(b+1,b+1+m,a[i])-b;
84         root[i]=Insert(root[i-1],1,m,t);
85     }
86     for(R i=1;i<=q;i++)
87     {
88         int x=rd(),y=rd(),k=rd();
89         R tmp=Query(root[x-1],root[y],1,m,k);
90         printf("%d\n",b[tmp]);
91     }
92     return 0;
93 }

我太蒟了所以加了一大波註釋(怕自己以後看不懂)

我太蒟了所以以上文字有什麼問題可以在評論區回覆

話說會有人看嗎QAQ