【1】 Thin Plate Spline editor - an example program in C++

https://elonen.iki.fi/code/tpsdemo/

Screenshot from the TPS demo

Based mostly on "Approximation Methods for Thin Plate Spline Mappings and Principal Warps" by Gianluca Donato and Serge Belongie, 2002.

Introduction to TPS

Thin Plate Spline, or TPS for short, is an interpolation method that finds a "minimally bended" smooth surface that passes through all given points. TPS of 3 control points is a plane, more than 3 is generally a curved surface and less than 3 is undefined.

The name "Thin Plate" comes from the fact that a TPS more or less simulates how a thin metal plate would behave if it was forced through the same control points.

Thin plate splines are particularily popular in representing shape transformations, for example, image morphing or shape detection/matching. (If you are interested in this application, see the separate example file in the bottom of this page.)

Consider two equally sized sets of 2D-points, A

In some cases, e.g. when the control point coordinates are noisy, you may want to relax the interpolation requirements slightly so that the resulting surface doesn't have to go exactly exactly through the control points. This is called regularization and is controlled by regularization parameter λ. If λ is zero, interpolation is exact and as it approaches infinity, the resulting TPS surface is reduced to a least squares fitted plane ("bending energy" of a plane is 0). In our example, the regularization parameter is also made scale invariant with an extra parameter α.

The math

Given set C of p 3D control points....

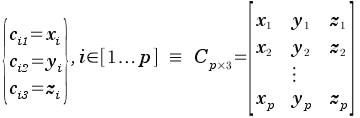
...and regularization parameter λ, solve unknown TPS weights w and a from linear equation system...

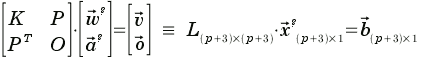
..., where K, P and O are submatrices and w, a, v and o are column vectors, given by:

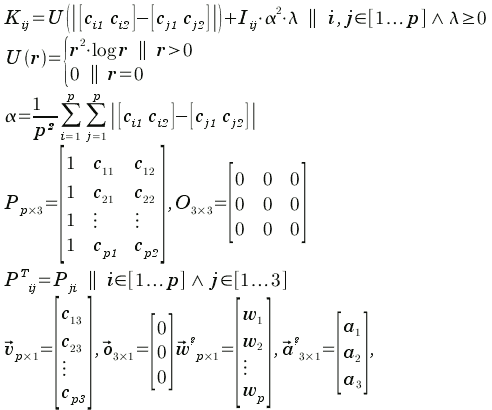
Note that L, and thus also its submatrix K, is symmetric so you can calculate elements for upper triangle only and copy them to the lower one. Also, α (mean of distances between control points' xy-projections) is a constant only present on the diagonal of K, so you can easily calculate it while filling up the upper and lower triangles. I is the standard unit diagonal matrix.

Then, once you know values for w and a, you can interpolate z for arbitrary points (x,y) from:

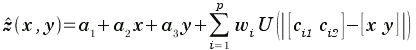
Bending energy (scalar) of a TPS is given by:

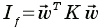
(download formulas in MML)

Speedup for large sets of control point

The LU-decomposition used in this example is a generic, direct solver that doesn't scale well as the size of the matrices grow large: it is O(N3). For large sets of control points, there are optimized (and much more complicated) methods for solving the Thin Plate Spline problem (or more generally, RBF or Radial Basis Function interpolation). They are based on iterative numerical solvers (like Gauss-Seidel or the conjugate gradient method) and the assumption that the effect of the control points is mainly local (i.e. only a few neighboring control points contribute majorly to interpolating a given point). These approximations scale well, in the order of O(N log N ) (albeit with pretty high constants).

For a good, readable introduction to these methods (preconditioning, Krylov subspace method, fast multipole algorithm) see: "Radial basis functions: theory and implementations" by Martin Dietrich Buhmann.

Example code

Tpsdemo is an example program, a graphical thin plate spline editor that demonstrates how to implement TPS interpolation in C++. It uses OpenGL + GLUT for graphics and Boost uBlas library for representing large matrices.

Download the whole source code and this explanation (tpsdemo-1.2.tar.gz) or browse individual files:

• main.cpp - code for solving the TPS weights, interpolating a grid with them and all OpenGL user interface stuff. Features:
  • mouse drive UI: click button 1 to add or elevate a point, hold down button 2 to rotate camera and click button 3 to show a popup menu
  • the shaded surface consists of 100x100 rectangles
  • shows XY plane as a grid and cartesian axes X,Y,Z in colors R,G,B
  • shows control points in relation to XY plane as bright yellow "pins"
  • keyboard commands: + and - tune regularization, d deletes selected control point, / and * zoom in/out
  • simple to modify to use as a generic 2D-function visualizer
• ludecomposition.h - a linear equation system solver for uBlas, using LU decomposition. I've heard that there's now a solver included in uBlas itself, though.
  • The package also contains a crude Gauss elimination solver , gauss-elim.h, but the LU decomposition is faster (and the code is also cleaner) so use it only if you run into numerical problems with LU.
• linalg3d.h - a one file long linear algebra library for simple 3D applications in C++. (uBlas is not very handly for simple 3D). Features:
  • scale and translation matrices, rotation matrices from euler angles and orientation vectors
  • transforming 3-vectors with 4x4 matrices
  • dot and cross product, norm and abs (length) of 3-vectors
  • simple plane-vector classification

The binary program only consists of one executable file and doesn't need any texture, model or other data files. To build and run it on a unix variant (with OGL and Boost installed of course), simply type:

g++ -c -O2 main.cpp && g++ main.o -lglut -lGL -lGLU -o tpsdemo && ./tpsdemo

2D point morph example

2d-morph.cpp - a class that fits a TPS on a given set of point displacements and applies (interpolates/extrapolates) the deformation to new sets of points. This also implements the TPS approximation algorithm #3 from Donato's and Belongie's paper. Unlike the other example, this one includes no visualization code at all.

License

Copyright (C) 2003, 2004, 2005 by Jarno Elonen

TPSDemo is Free Software / Open Source with a very permissive license:

Permission to use, copy, modify, distribute and sell this software and its documentation for any purpose is hereby granted without fee, provided that the above copyright notice appear in all copies and that both that copyright notice and this permission notice appear in supporting documentation. The authors make no representations about the suitability of this software for any purpose. It is provided "as is" without express or implied warranty.

(This page and images on it count as documentation of the software and are thus under the same license.)