OO has got a array A of size n ,defined a function f(l,r) represent the number of i (l<=i<=r) , that there’s no j(l<=j<=r,j<>i) satisfy a i mod a j=0,now OO want to know

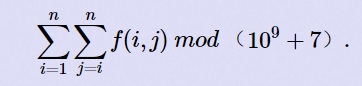
Input
There are multiple test cases. Please process till EOF.
In each test case:
First line: an integer n(n<=10^5) indicating the size of array
Second line:contain n numbers a i(0<a i<=10000)
Output
For each tests: ouput a line contain a number ans.
Sample Input
5
1 2 3 4 5
Sample Output
23

題意：

給你n個數，讓你求如圖所示的一個累加，f(l,r)表示問你在l到r區間內有多少個數，使得這個區間任意其他數不整除這個數.

題解：

先預處理因子，在for一遍，求每個數貢獻的區間，找到左邊它的第一個因子，右邊它的第一個因子，然後它的貢獻就是以他為端點的區間數+不以他為端點包括他的區間數= $\left(ll\right)($

r i g h t − l e f t − 1 ) + ( l l ) ( i − l e f t − 1 ) ∗ ( r i g h t − i − 1 ) (ll)(right-left-1)+(ll)(i-left-1)*(right-i-1)

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e9+7;
vector<int>vec[10005],yz[10005];
void init()
{
    for(int i=1;i<=10000;i++)
    {
        for(int j=1;j<=sqrt(i);j++)
        {
            if(i%j==0)
            {
                yz[i].push_back(j);
                if(j*j!=i&&j!=1)
                    yz[i].push_back(i/j);
            }
        }
    }

}
int a[100005];
int main()
{
    init();
    int n;
    while(~scanf("%d",&n))
    {
        for(int i=1;i<=10000;i++)
            vec[i].clear(),vec[i].push_back(0);
        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]),vec[a[i]].push_back(i);
        //for(int i=0;i<vec[1].size();i++)
            //cout<<vec[1][i]<<endl;
        for(int i=1;i<=10000;i++)
            vec[i].push_back(n+1);
        ll ans=0;
        for(int i=1;i<=n;i++)
        {
            int left=0,right=n+1;
            if(a[i]!=1)
            {
                for(int j=0;j<yz[a[i]].size();j++)
                {
                    int num=yz[a[i]][j];
                    //for(int k=0;k<vec[a[i]].size();k++)
                        //cout<<a[i]<<": "<<yz[a[i]][j]<<": "<<vec[a[i]][k]<<endl;
                    int p=upper_bound(vec[num].begin(),vec[num].end(),i)-vec[num].begin();
                    left=max(left,vec[num][p-1]);
                    right=min(right,vec[num][p]);
                }
            }
            int p=lower_bound(vec[a[i]].begin(),vec[a[i]].end(),i)-vec[a[i]].begin();
            left=max(left,vec[a[i]][p-1]);
            //cout<<vec[a[i]][p+1]<<endl;
            right=min(right,vec[a[i]][p+1]);
            (ans+=(ll)(right-left-1)+(ll)(i-left-1)*(right-i-1))%=mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}