語音學習筆記（四）【傳統聲學模型】

 

1.混合高斯模型（GMM） 
當使用混合高斯隨機變數的分佈用於匹配語音特徵時，就形成了混合高斯模型（GMM）。 
1.1隨機變數 
1）隨機變數可以理解為從隨機實驗到變數的一個對映； 
2）隨機變數所有可能的取值成為域； 
3）連續隨機變數的概率密度函式（Probability density function，PDF）：p（x） 
4）隨機變數在x=a處的累計分佈函式 ：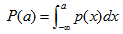 
 
1.2 高斯分佈和混合高斯隨機變數 
1）高斯分佈 
標量：若隨機變數x的概率密度函式是： 

 
那麼它服從正態分佈或高斯分佈，記為： 
 
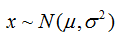
向量/向量：對於高斯分佈的隨機變數向量x=（x1,x2,…,xD）T,也成為多元或向量值高斯隨機變數，其聯合概率密度函式為： 
 
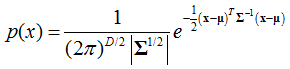
同樣，記為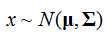： （均值，協方差） 
2）混合高斯分佈 
標量：服從混合高斯分佈的隨機變數x，其概率密度函式為：（M個高斯） 
 
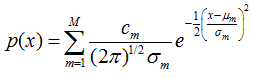
其中混合權重為正實數，其和為1： 
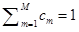
混合高斯分佈最明顯的性質是他的多模態（M大於1），不同於高斯分佈的單模態（M=1），這使得混合高斯模型足以描述很多顯示出多模態性質的物理資料，比如語音資料，而單高斯分佈則不合適。 
向量/向量：多變數的多元混合高斯分佈，即，服從高斯分佈的隨機變數向量，其聯合概率密度函式為： 
 
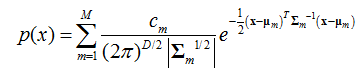
在DNN出現之前，GMM是提升語音識別系統性能的一個關鍵，且一般M為一個先驗值。 
如果變數x的維度D很大，比如語音識別中的特徵40維，那麼使用全協方差矩陣（非對角）（∑m）將引入大量引數（大約M x D^2）。為了減少這個數量，可以使用對角協方差矩陣。對角協方差矩陣極大簡化了計算量。將全協方差矩陣近似為對角協方差矩陣看似是使用了各維度不相關的假設，實際是一種誤導，因為，混合高斯模型具有多個高斯成分，雖然每個成分都使用了對角協方差矩陣，但總體上至少可以有效的描述由一個使用全協方差矩陣的單高斯模型所描述的向量維度相關性。