我們知道遞迴演算法非常低效，低效的原因在於遞迴的過程會產生冗餘計算。

拿我們熟悉的斐波那契數列為例，計算公式為：F(n) = F(n - 1) + F(n - 2)，其中F(0) = F(1) = 1。

例如計算F(5)的執行過程：

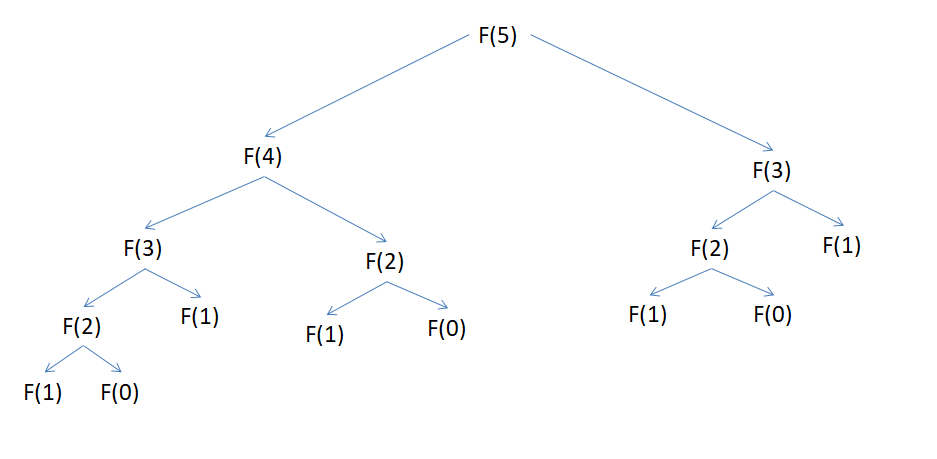
在此過程中，F(4) 執行了1次；F(3)執行了2次；F(2)執行了3次；F(1)執行了5次；F(0)執行了3次;由此可見，遞迴演算法低效的原因。

為了提高執行效率，通常可以用一個表來代替遞迴，例如 C++ 中的vector。

這裡舉兩個例子，分別以遞迴和非遞迴兩種方式實現：

問題一：菲波那切數列

第一種方法：遞迴實現

int fib(int
 
 n)
{
    if(n <= 1)
        return 1;

    return fib(n - 1) + fib(n - 2);
}

第二種方法：非遞迴實現——用表代替遞迴

int fibona(int n)
{
    if(n <= 1)
        return 1;

    vector<int> aNumber(n + 1,0);
    aNumber[0] = 1;
    aNumber[1] = 1;
    for (int i = 2;i <= n;i++)
    {
        aNumber[i] 
 
=  aNumber[i - 1] + aNumber[i - 2];
    }

    return aNumber[n];
}

問題二：計算數學公式

演算法實現此公式：

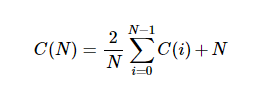
第一種方法：遞迴實現

float eval1(int n)
{
    if(n == 0)
        return 1;

    float sum = 0;
    for (int i = 0; i < n;i++)
        sum += eval1(i);
    return 2 * sum / n + n;
}

第二種方法：非遞迴實現——用表代替遞迴

1. 複雜度是O(N * N)

float eval2(int n)
{
    vector<float> aNumber(n + 1,0);
    aNumber[0] = 1;

    for (int i = 1; i <= n;i++)
    {
        float fSum = 0;
        for (int j = 0; j < i;j++)
        {
            fSum += aNumber[j];
        }
        aNumber[i] = 2 * fSum/i + i;
    }

    return aNumber[n];
}

2. 最完美的方案， 複雜度是O(N)

float eval3(int n)
{
    vector<int> aNumber(n + 1,0);
    aNumber[0] = 1;

    float fSum = 0;
    for (int i = 1;i <= n;i++)
    {
        fSum += aNumber[i - 1];
        aNumber[i] = 2 * fSum/i + i;
    }

    return aNumber[n];
}