Time Limits: 2000 ms Memory Limits: 262144 KB

Description

Input

Output

Sample Input

Sample Input1：
4 3 9 6
5 8 7 7

Sample Input2：
見下發檔案中的 ex_pow2.in/out.

Sample Output

Sample Output1：
0

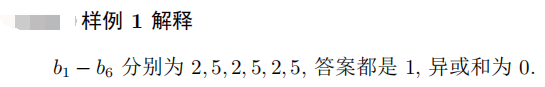
Sample Output2：

Data Constraint

Solution

多次給出同一個數的指數，求這個數的冪
因為是同一個數嘛，肯定不可以每次都用快速冪，這太浪費時間了
於是我們可以先預處理 $a$

Code

#include<algorithm>
#include<cstdio>

#define fo(i,a,b) for(int i=a;i<=b;++i)
#define fd(i,a,b) for(int i=a;i>=b;--i)
#define ll long long

using namespace std;

const int N=1e6;
ll a,p,q,k,b,l,m,c,d[N+5],e[N+5];

int main()
{
	freopen("pow.in","r",stdin);
	freopen("pow.out","w",stdout);
	scanf("%lld%lld%lld%lld",&a,&p,&q,&k);
	scanf("%lld%lld%lld%lld",&b,&l,&m,&c);
	d[0]=1; fo(i,1,N) d[i]=d[i-1]*a%p;
	e[0]=1; fo(i,1,N) e[i]=e[i-1]*d[N]%p;
	ll ans=0;
	fo(i,1,q/k)
	{
		ll sum=0;
		fo(j,(i-1)*k+1,i*k)
		{
			b=(m*b%l+c)%l;
			sum^=d[b%N]*e[b/N]%p;
		}
		ans^=sum;
		printf("%lld\n",ans);
	}
}