深入理解計算機系統 第二章 資訊的表示和處理
欣哥劃的重點:
第二章比較難,建議至少掌握下面幾個知識點: 1. 位元組順序 : 大端和小端 2. 執行 圖2-24, 圖2-25程式 show-bytes.c 觀察結果,看看有什麼問題 3. 理解布林運算,位運算 4. 理解無符號數和有符號數, 給一個數,能計算出補碼 5. 理解浮點數的表示法,給一個十進位制小數,能轉換成二進位制的浮點數表示
由於第二章知識點很多,上班又比較忙,所以按欣哥劃的重點來閱讀。
本週看了 3 個點:
1、位元組順序:大端和小端
2、理解布林運算,位運算
3、理解無符號數和有符號數,給一個數,能計算出補碼
下面按點寫筆記:
1、位元組順序:大端和小端
前提:
對於跨越多位元組地址的物件,在幾乎所有的機器上,都會被儲存為連續的位元組序列,物件的地址為所使用的位元組中最小的地址。
先說大端和小端的定義
小端法:最低有效位元組在最前面的方式
大端法:最高有效位元組在最前面的方式
舉例說明:
對於數 0xA1FE,它在計算機中會被儲存為連續的兩個位元組,當 A1 被儲存在前時,即為大端表示法;當 FE 被儲存在前時,即為小端表示法
在這個例子中,A1 為最高有效位元組,FE 為最低有效位元組
注:
現在我們假設有一個 w 位的二進位制數,只要 w 大於 8,它就總能被表示為多個位元組(即,從右到左,8 位結合為 1 位元組,最後不夠 8 位的部分,在左邊用 0 補齊)
總結:
結合前提和定義,我們可以說,地址為最高有效位元組的多位元組物件使用的是大端法,反過來,地址為最低有效位元組的多位元組物件使用的是小端法
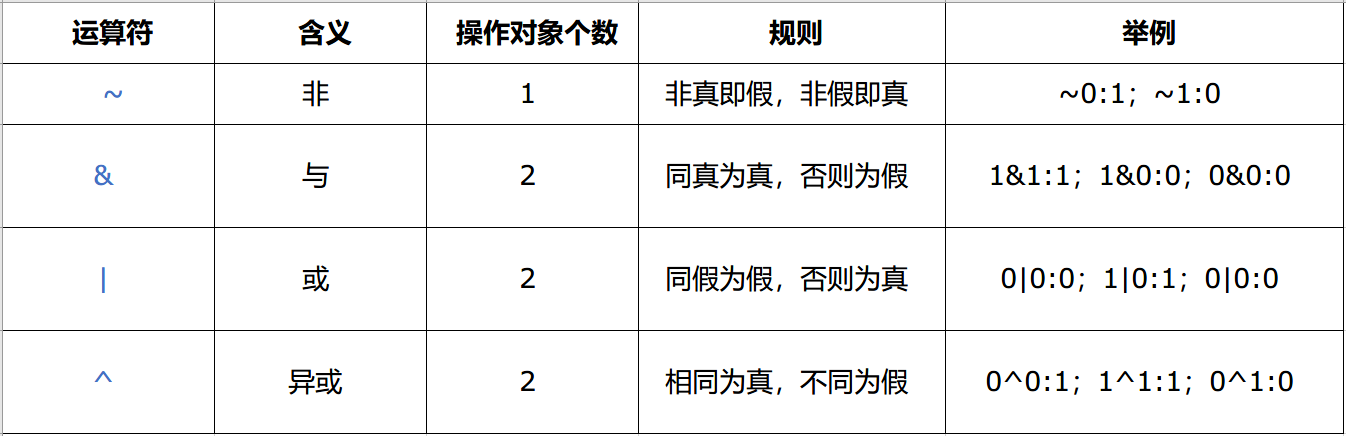
2、布林運算,位運算
主要要記住 4 個運算子的意義,對相應的規則整理如下
3、理解無符號數和有符號數,給一個數,能計算出補碼
無符號數:所有的位都表示數值
有符號數:第一位是符號位(0 為正,1 為負),其餘都表示數值
補碼計算例項:
負數 6 的原碼為 1000 0110
其反碼為 1111 1001
其補碼為 1111 1010
補充一下原碼、反碼和補碼的概念:
原碼
就是符號位加上真值的絕對值, 即用第一位表示符號, 其餘位表示值
反碼:
正數的反碼是其本身
負數的反碼是在其原碼的基礎上, 符號位不變,其餘各個位取反
補碼:
正數的補碼就是其本身
負數的補碼是在其原碼的基礎上, 符號位不變, 其餘各位取反, 最後+1. (即在反碼的基礎上+1)
希望在下週的閱讀中,能解決以下問題:
原碼、反碼、補碼是隻針對有符號數嗎?無符號數有沒有這三種編碼方式?
