Luogu P3616 【富金森林公園】
阿新 • • 發佈:2018-11-08
我們首先考慮一塊石頭高度變化對每個高度的查詢的答案的影響,
即我們要記錄,對於每個高度的查詢的答案
所以要離散化高度(不然哪開的下陣列啊)
不難發現,一次變化的對於不同高度的影響,對於一段連續高度是相同的
即一次修改操作,對於一段連續高度的答案,影響相同,滿足區間修改性質
就決定是你了,樹狀陣列
具體來說,考慮修改位置修改前後和兩邊的高度關係
但是情況很多,不妨把修改操作換成先刪除(把高度降為0),再插入
考慮刪除,插入的話,反過來就好,中間的是刪除位置
情況1:中間比兩邊低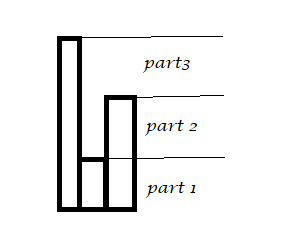
最簡單的情況,不難發現,刪除掉中間的只能讓高度為$part1$的區間的答案$+1$,因為它割裂了兩邊的連續區間
情況2:中間比兩邊高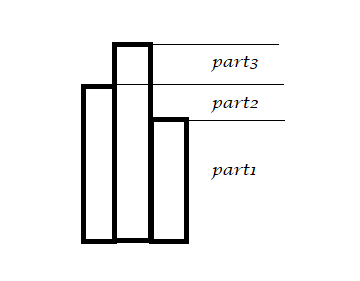
最高的區間影響就很廣了
對於$part1:$它的刪除會割裂兩邊的區間$val~of~part1++$
對於$part2:$因為兩邊沒有構成連續區間,所以沒有影響
對於$part3:$原來是有露出來的,現在沒了,當然要減掉了
情況3:中間的高度也中等
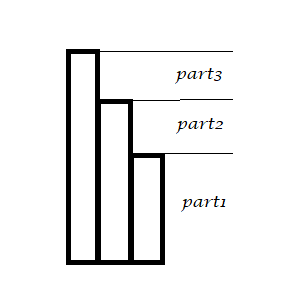
也很簡單了,只對$part1$有影響
然而這樣處理的只是答案的變化,我們還需要統計初始答案
還是考慮高度變化對答案的影響,不難發現,隨著高度上升,未被覆蓋的點的個數是單調不升的
按高度開$vector$,把每個高度恰好被覆蓋的所有位置扔進去
從小到大列舉高度,先將這個高度的答案設為上一個高度的答案,取出這個高度恰好被覆蓋的所有位置,統計這個位置的影響
如果它比兩邊高,類比上面情況2,答案減一
低呢,答案加一
這樣我們就解決了這個問題
上程式碼:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
using namespace std;
const int maxn=2e5+10;
vector<int>v[2*maxn];
int pre[2*maxn],n,m,a[maxn],mp[2*maxn],op[maxn],cnt,b[maxn],d[maxn],c[2*maxn];
bool vis[2*maxn];
int lowbit(int
