Double Array Trie(一)
Trie是一種常見的資料結夠,可以實現字首匹配(hash是不行的),而且對於詞典搜尋來說也是O(1)的時間複雜度,雖然比不上Hash,但是空間會省不少。
Trie樹主要應用在資訊檢索領域,非常高效。今天我們講Double Array Trie,請先把Trie樹忘掉,把資訊檢索忘掉,我們來講一個確定有限自動機(deterministic finite automaton ,DFA)的故事。所謂“確定有限自動機”是指給定一個狀態和一個變數時,它能跳轉到的下一個狀態也就確定下來了,同時狀態是有限的。請注意這裡出現兩個名詞,一個是“狀態”,一個是“變數”,下文會舉例說明這兩個名詞的含義。
舉個例子,假設我們一共有10個漢字,每個漢字就是一個“變數”。我們為每個漢字編個序號。
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 啊 |
阿 |
埃 |
根 |
膠 |
拉 |
及 |
廷 |
伯 |
人 |
表1. “變數”的編號
這10個漢字一共可以構成6個詞語:啊,埃及,阿膠,阿根廷,阿拉伯,阿拉伯人。
這裡的每個詞以及它的任意字首都是一個“狀態”,“狀態”一共有10個:啊,阿,埃,阿根,阿根廷,阿膠,阿拉,阿拉伯,阿拉伯人,埃及
我們把DFA圖畫出來:
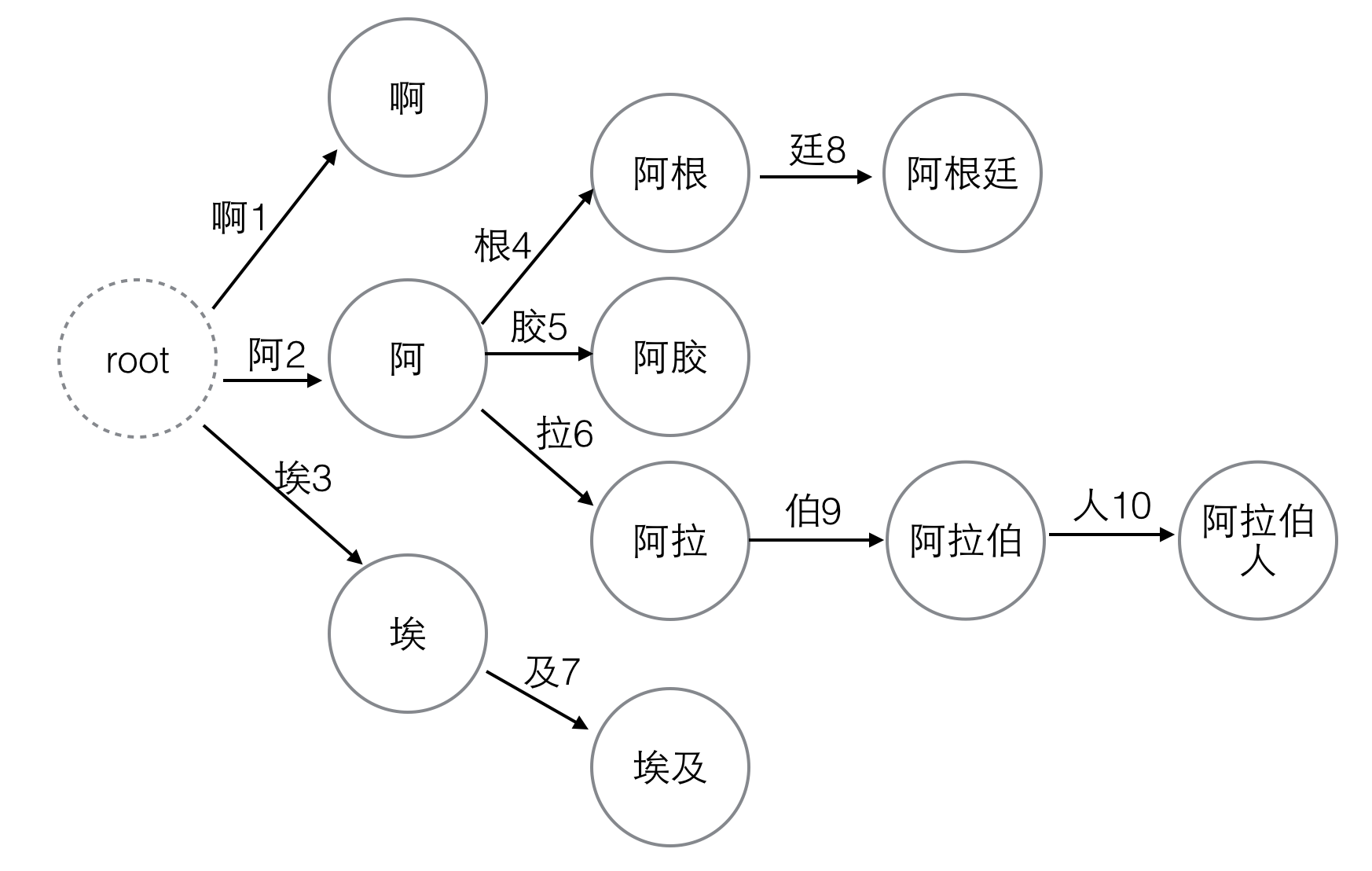
圖1. DFA,同時也是Trie樹
在圖中每個節點代表一個“狀態”,每條邊代表一個“變數”,並且我們把變數的編號也標在了圖中。
下面我們構造兩個int陣列:base和check,它們的長度始終是一樣的。陣列的長度定多少並沒有嚴格的規定,反正隨著詞語的插入,陣列肯定是要擴容的。說到陣列擴容,大家可以看一下java中HashMap的擴容策略,每次擴容陣列的長度都會變為2的整次冪。HashMap中有這麼一個精妙的函式:
| 1 2 3 4 5 6 7 8 9 10 |
|
回到今天的正題,我們不妨把double array的初始長度就定得大一些。兩陣列元素初始值均為0。
double array的初始狀態:
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| state |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
把詞新增到詞典的過程就給base和check陣列中各元素賦值的過程。下面我們層次遍歷圖1所示的Trie樹。
step1.
第一層上取到3個“狀態”:啊,阿,埃。把這3個狀態按照其對應的變數的編號(查表1)放到state陣列中。
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| state |
啊 |
阿 |
埃 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
step2.
當存在狀態轉移![]() 時,有
時,有
| 1 2 |
|
其中s和t代表某個狀態在陣列中的下標,c代表變數的編號。
此時層次遍歷來到了圖1所示DFA的第二層,我們看到“阿”的子節點有“阿根”、“阿膠”、“阿拉”,已知狀態“阿”的下標是2,變數“根”、“膠”、“拉”的編號依次是4、5、6,下面我們要給base[2]賦值:從小到大遍歷所有的正整數,直到發現某個數正整k滿足base[k+4]=base[k+5]=base[k+6]=check[k+4]=check[k+5]=check[k+6]=0。(查詢到base和check等於0的, 是因為0代表該位沒有被使用)得到k=1,那麼就把1賦給base[2],同時也確定了狀態“阿根”、“阿膠”、“阿拉”的下標依次是k+4、k+5、k+6,即5、6、7,而且check[5]=check[6]=check[7]=2。
同理,“埃”的子節點是“埃及”,狀態“埃”的下標是3,變數“及”的編號是7,此時有check[1+7]=base[1+7]=0,所以base[3]=1,狀態“埃及”的下標是8,check[8]=3。
遍歷完DFA的第二層後得到下表:
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| state |
啊 |
阿 |
埃 |
|
阿根 |
阿膠 |
阿拉 |
埃及 |
|
|
|
|
|
|
|
|
|
|
|
step3.
重複step2,層次遍歷完整查詢樹之後,得到:
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
3 |
5 |
7 |
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| state |
啊 |
阿 |
埃 |
|
阿根 |
阿膠 |
阿拉 |
埃及 |
阿根廷 |
阿拉伯 |
阿拉伯人 |
|
|
|
|
|
|
|
|
step4.
最後遍歷一次DFA,當某個節點已經是一個詞的結尾時,按下列方法修改其base值。
| 1 2 3 4 |
|
得到:
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
-1 |
1 |
1 |
0 |
1 |
-6 |
1 |
-8 |
-9 |
-1 |
-11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
3 |
5 |
7 |
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| state |
啊 |
阿 |
埃 |
|
阿根 |
阿膠 |
阿拉 |
埃及 |
阿根廷 |
阿拉伯 |
阿拉伯人 |
|
|
|
|
|
|
|
|
double array建好之後,如果詞典中又動態地添加了一個新詞,比如“阿拉根”,那麼“阿拉”的所有子孫節點在double array中的位置要重新分配。

圖2. 動態新增一個詞
首先,把“阿拉伯”和“阿拉伯人”對應的base、check值清0,把“阿拉伯”和“阿拉伯人”從state陣列中刪除掉,把“阿拉”的base值清0。
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
-1 |
1 |
1 |
0 |
1 |
-6 |
0 |
-8 |
-9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
3 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| state |
啊 |
阿 |
埃 |
|
阿根 |
阿膠 |
阿拉 |
埃及 |
阿根廷 |
|
|
|
|
|
|
|
|
|
|
然後,按照上面step2所述的方法把“阿拉伯”、“阿拉根”插入到double array中。變數“根”、“伯”的編號是4和9,滿足base[k+4]=base[k+9]=check[k+4]=check[k+9]=0的最小的k是6,所以base[7]=6,“阿拉伯”和“阿拉根”對應的下標是10和15。同理把“阿拉伯人”插入到double array中。
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
-1 |
1 |
1 |
0 |
1 |
-6 |
6 |
-8 |
-9 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
3 |
5 |
7 |
15 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
| state |
啊 |
阿 |
埃 |
|
阿根 |
阿膠 |
阿拉 |
埃及 |
阿根廷 |
阿拉根 |
阿拉伯人 |
|
|
|
阿拉伯 |
|
|
|
|
最後,遍歷圖2所示的DFA,當某個節點已經是一個詞的結尾時按照step4中的方法修改其base值。
| 下標 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
| base |
-1 |
1 |
1 |
0 |
1 |
-6 |
6 |
-8 |
-9 |
-10 |
-11 |
0 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
| check |
0 |
0 |
0 |
0 |
2 |
2 |
2 |
3 |
5 |
7 |
15 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
| state |
啊 |
阿 |
埃 |
|
阿根 |
阿膠 |
阿拉 |
埃及 |
阿根廷 |
阿拉根 |
阿拉伯人 |
|
|
|
阿拉伯 |
|
|
|
|
double array建好之後,如何查詢一個詞是否在詞典中呢?
比如要查“阿膠及”,每個字的編號是已知的,我們畫出狀態轉移圖。

變數“阿”的編號是2,base[2]=1,變數“膠”的編號是5,base[2]+5=6,我們檢查一下check[6]是否等於2。check[6]確實等於2,則繼續看下一個狀態轉移。同時我們發現base[6]是負數,這說明“阿膠”已經是一個完整的詞了。
繼續看下一個狀態轉移,base[6]=-6,負數取其相反數,base[6]=6,變數“及”的編號是7,base[6]+7=13,我們檢查一下check[13]是否等於6,發現不滿足,則“阿膠及”不是一個詞,甚至都是不是任意一個詞的字首。
