再談韋伯/費希納定律以及我對數學公式的理解
浙江溫州皮鞋溼,下雨進水不會胖!
今年年初的時候,我寫過一篇關於費希納定律的文章,當時也算是即興寫作,記得本來是看了個電影,電影到高潮的時候喝了一瓶真露看到結束,然後有點微暈,就寫了那篇文章:
韋伯-費希納定律與對數關係的深意 :https://blog.csdn.net/dog250/article/details/79111759
酒後之作難免不嚴謹,太多些隨意的東西,前幾日有人問到這篇文章中關於費希納定律的細節問題,我就決定就這個問題再寫幾筆。
其中,比較不好理解的是費希納定律的公式是怎麼來的。這就不得不從心理學的角度開始說起。
溫水煮青蛙都應該知道,同樣的水溫,如果是逐漸加熱的,青蛙可能還會不亦樂乎地游泳,但是你要是直接把青蛙扔進這個水溫的鍋裡,青蛙一定會跳起來!
韋伯發現了一個一般性的現象,最終他假設,人們對物理刺激的感覺是離散化的,針對每一個強度的物理刺激,在該刺激強度下,若要人們有所感覺,需要額外物理刺激強度和當前物理刺激強度成正比。 韋伯定律即:
其中 為韋伯係數。
舉個例子,我抱著10斤的重物,你再給我偷偷加1兩我是沒感覺的,加2兩也是沒有感覺的,一旦你加了1斤,我就會發現,怎麼變重了。那麼根據上面的韋伯定律公式,就是:
此時,可以得出,我的韋伯係數就是 ,那麼現在,如果我抱著100斤的重物(假設我能抱得動),你給我添多重的物品,我能感覺得到。
很簡單,套用上面的公式即可:
可以得到, 等於10斤,也就是說,你再加10斤的重量才能讓我感覺到重了。
韋伯定律揭示了一個關係,即 當前物理刺激和引起你感覺的額外物理刺激之間的關係。值得注意的是,上面這個韋伯定律的表示其實是費希納給出的,而韋伯當時只是給出了一組實驗以及一個描述。
為什麼費希納要總結這樣一個公式?
因為費希納希望得到一個更加普遍的關係,即 物理刺激的度量和心理感覺的度量之間的關係。這是一個定量的關係,他希望能用數學表達出精確的關係。所以,費希納總結了韋伯的工作,並且將其命名為 韋伯定律。
費希納為了得到更加普遍的物理刺激量和心理感覺量之間的關係,在他自己整理出的韋伯定律的式子的基礎上,提出了自己的假設。
我不是費希納,但是我也許能感覺到他當時的設想,因為如果是我的話,我也會這麼想。
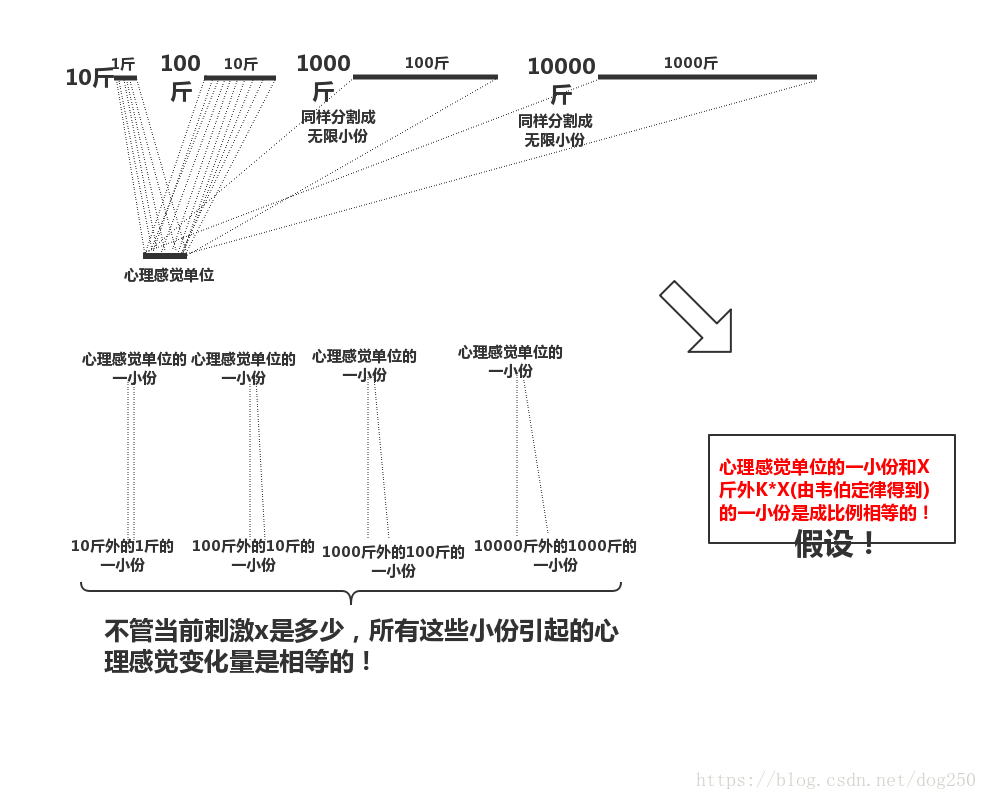
還是以10斤到11斤的重量變化,100斤到110斤的重量變化為例。雖然10斤到11斤只差了1斤,而100斤到110斤差了10斤,但是 在效果上卻是相同的。 二者都是引發了 同樣的心理感覺變化。進一步地,由韋伯定律可知,重量從1000斤到1100斤,也會引發與前二者相同的心理感覺變化。如果我們把能感受到的心理感覺變化視為一個基本單位,物理刺激和它的關係如下圖所示:
非常容易理解,既然1斤,10斤,100斤,1000斤都能引起相同的心理感覺效果,那麼將它們無限切割,對應到連續統動力學上,不管是1斤還是10斤,100斤,其中每一份小的物理刺激的增加,也同樣能帶來 小的且相同的心理感覺的變化 (只是這種心理學上微妙的變化沒能引發我們的感覺而已,量變在 的時候才會引起質變)。
按照這個假設,設心理感覺量為 ,在當前刺激 下,能引發心理感覺的額外刺激量為 ,根據韋伯定理,上圖中的感覺量小份 則為:
寫成微積分的形式就是,設 ,則有:
解方程則有:
哇!原來是對數關係!
就這樣。一開始費希納並不知道這是個對數關係,在韋伯的工作的基礎上,結合自己的實驗以及大膽的假設,才最終推匯出了這個對數關係,最終我們通過這個對數關係可以獲知:人的感覺滯後於物理刺激的變化。
最後,人們得到的東西實在是太多了,這個費希納定律解釋了為什麼長髮突然刮成光頭會很爽,這也解釋了為什麼食色性在頻繁滿足後會厭倦,等等等等,不一而足。
… 很晚了。不過…
我得說說我對這種數學公式的理解。
幾乎任何可以用數學式子表示的定律,都是從 一個假設 開始的,之後加上一個 求證 的過程,是為 大膽假設,小心求證 。基於最初的假設,大段大段地整理數學式子,最終,哇,這麼漂亮的一個結論!
也就是說,就算是作者本人可能一開始也不知道最終的結論性的數學式子長什麼樣子,他一開始只是假設幾條簡單的他認為自洽,和諧的假設,然後用數學技巧一步一步推導,最後得到一個化簡後的式子。如果大自然是簡單優美的,那麼能正確描述大自然的式子一定就是簡單優美的,至少迄今為止,還沒看到哪個科學家喜歡複雜。
所以說,像平方反比律,像 這種,都是結論,而不是前提。最終,當他有了這種簡單式子表示的結論後,他便可以從式子的數學性質來獲取其物理意義的關聯了,就是這樣,而不是反過來。
但是我們的學校在教這些定律時,恰恰是反過來教的,老師一般會先給出式子,然後給出一個證明,最後做幾道使用這個式子解答的作業題,老師會讓我們把式子背下來,以應對考試之需。
由於大腦容量有限,一旦考完試,這些東西就再也用不到了,於是就都忘了…其實正確的做法中應該包含一個故事的,即人們碰到了什麼問題,然後有個科學家提出了什麼樣的假設,他如何用數學表示他的假設,他如何一步一步地根據他的假設得到最終的那個老師讓我們背下來的公式。是這樣。
我記得很清楚,高中的物理老師說的那句話,一定要培養大段大段整理數學式子的能力, 後來仔細想想,這是非常必要的,因為這個能力可能真的就能帶到一個美好的新世界,在這個世界裡,所有的結論都是那麼的簡單,優美,和諧。
皮鞋沒有登上,露著白襪子!