線段樹優化連邊

要求點 \(x\) 向區間 \([L, R]\) 連邊， 一次的複雜度上限為 \(O(n)\)
然後弄成線段樹的結構

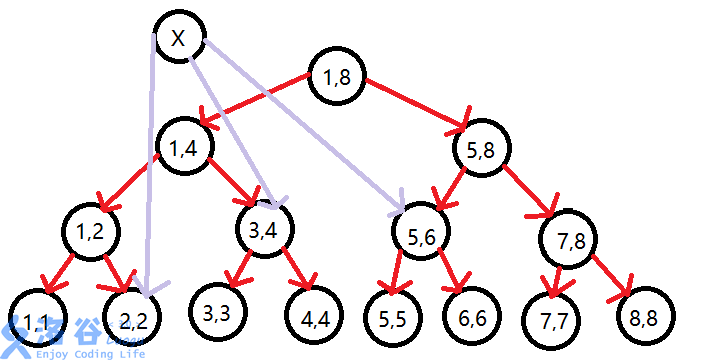
先父子連邊邊權為 \(0\)
這樣連邊就只需要連父親就可以等效於連了區間內每個點
空間複雜度為線段樹大小， 一次區間連邊時間複雜度為 \(O(\log n)\)
這是連入邊， 連出邊的話反向建線段樹內邊即可

CF786B Legacy

預設情況下他不能用這把槍開啟任何傳送門。在網路上有q個售賣這些傳送槍的使用方案。每一次你想要實施這個方案時你都可以購買它，但是每次購買後只能使用一次。每個方案的購買次數都是無限的。

網路上一共有三種方案可供購買： 1.開啟一扇從星球v到星球u的傳送門； 2.開啟一扇從星球v到標號在[l,r]區間範圍內任何一個星球的傳送門。(即這扇傳送門可以從一個星球出發通往多個星球) 3.開啟一扇從標號在[l,r]區間範圍內任何一個星球到星球v的傳送門。(即這扇傳送門可以從多個星球出發到達同一個星球)

Rick並不知道Morty在哪兒，但是Unity將要通知他Morty的具體位置，並且他想要趕快找到通往所有星球的道路各一條並立刻出發。因此對於每一個星球(包括地球本身)他想要知道從地球到那個星球所需的最小錢數。

Solution

線段樹優化連邊即可

Code

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
#define LL long long
#define REP(i, x, y) for(LL i = (x);i <= (y);i++)
using namespace std;
LL RD(){
    LL out = 0,flag = 1;char c = getchar();
    while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
    while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
    return flag * out;
    }
const LL maxn = 100019 << 2, inf = 0xfffffffffffffff;
LL head[maxn],nume = 1;
struct Node{
    LL v,dis,nxt;
    }E[maxn << 3];
void add(LL u,LL v,LL dis){
    E[++nume].nxt = head[u];
    E[nume].v = v;
    E[nume].dis = dis;
    head[u] = nume;
    }
LL num, nr, s;
#define lid (id << 1)
#define rid (id << 1) | 1
LL tot;
struct seg_tree{
    LL l, r;
    LL Index[2];
    }tree[maxn << 2];
void build(LL id, LL l, LL r){
    tree[id].l = l, tree[id].r = r;
    if(l == r){
        tree[id].Index[0] = tree[id].Index[1] = l;
        return ;
        }
    tree[id].Index[0] = ++tot;//入邊
    tree[id].Index[1] = ++tot;//out
    LL mid = (l + r) >> 1;
    build(lid, l, mid), build(rid, mid + 1, r);
    add(tree[id].Index[0], tree[lid].Index[0], 0);
    add(tree[id].Index[0], tree[rid].Index[0], 0);
    add(tree[lid].Index[1], tree[id].Index[1], 0);
    add(tree[rid].Index[1], tree[id].Index[1], 0);
    }
void IG(LL id, LL u, LL dis, LL l, LL r, LL o){//0 --> in, 1 --> out
    if(tree[id].l == l && tree[id].r == r){
        if(o == 2)add(u, tree[id].Index[0], dis);
        else add(tree[id].Index[1], u, dis);
        return ;
        }
    LL mid = (tree[id].l + tree[id].r) >> 1;
    if(mid < l)IG(rid, u, dis, l, r, o);
    else if(mid >= r)IG(lid, u, dis, l, r, o);
    else IG(lid, u, dis, l, mid, o), IG(rid, u, dis, mid + 1, r, o);
    }
void init(){
    num = RD(), nr = RD(), s = RD();
    tot = num;
    build(1, 1, num);
    REP(i, 1, nr){
        LL cmd = RD(), u = RD();
        if(cmd == 1){
            LL v = RD(), dis = RD();
            add(u, v, dis);
            }
        else{
            LL l = RD(), r = RD(), dis = RD();
            IG(1, u, dis, l, r, cmd);
            }
        }
    }
LL d[maxn];
bool vis[maxn];
void Djs(LL s){
    REP(i, 1, tot)d[i] = inf;
    priority_queue<pair<LL, LL> >Q;
    d[s] = 0;
    Q.push(make_pair(-d[s], s));
    while(!Q.empty()){
        LL u = Q.top().second;Q.pop();
        if(vis[u])continue;
        vis[u] = 1;
        for(LL i = head[u];i;i = E[i].nxt){
            LL v = E[i].v, dis = E[i].dis;
            if(d[u] + dis < d[v]){
                d[v] = d[u] + dis;
                Q.push(make_pair(-d[v], v));
                }
            }
        }
    }
void solve(){
    Djs(s);
    REP(i, 1, num){
        if(d[i] == inf)printf("-1 ");
        else printf("%lld ", d[i]);
        }
    puts("");
    }
int main(){
    init();
    solve();
    return 0;
    }