http://poj.org/problem?id=2777 

題意：

區間1到n，起始顏色都為1，每次更新一段區間的顏色（C left right val），問區間內的顏色有幾種（P left right）

思路：

這題給的顏色種類最多30，可以想到用位運算來求解，顏色是1到n那麼，我們用二進位制1<<(n-1)來表示顏色，

比如顏色1 ：1，2:10，3：100，4：1000

然後關鍵是怎麼求區間顏色的種類數，

可以發現一段區間的顏色是1 2

那麼我們用或運算|，來把這段區間的顏色值都或起來，得到11，這時候，1的個數就是區間顏色的種類

在比如1 2 =》1 1

1 3 =》1 0 1

那麼1 2 1 3=》1 1 1（3種顏色）

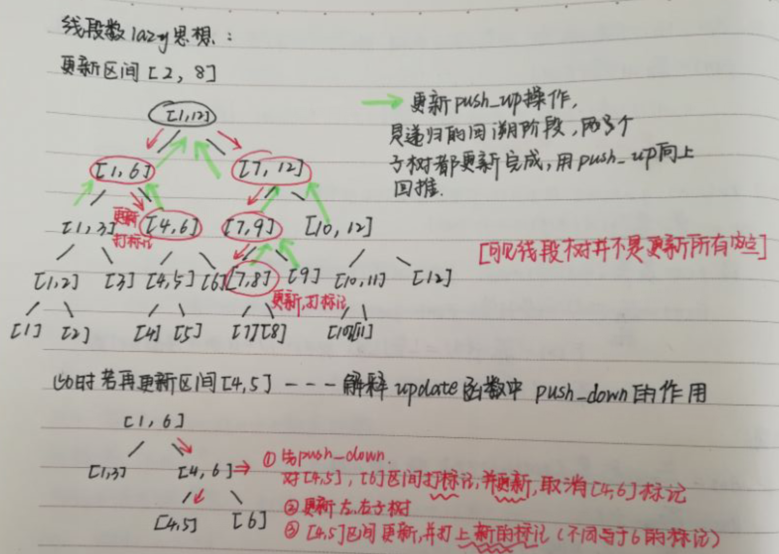
（感覺這題對lazy思想又進一步的理解了，總結如下圖：）

（還有一個坑，就是輸入的時候要判斷left和right，保證left<right……）

程式碼如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<cmath>
#include<set>
#define ll long long
using namespace std;
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int N=1000005;
int sum[N<<2],flag[N<<2];

void push_up(int rt){
    sum[rt]=sum[rt<<1]|sum[rt<<1|1];
}

void build(int l,int r,int rt){
    sum[rt]=1;
    if(l==r)return ;
    int m=(l+r)>>1;
    build(lson);
    build(rson);
}

void push_down(int rt){
    if(flag[rt]){
        int C=flag[rt];
        flag[rt<<1]=C;
        flag[rt<<1|1]=C;
        sum[rt<<1]=1<<(C-1);
        sum[rt<<1|1]=1<<(C-1);
        flag[rt]=0;
    }
}

void update(int L,int R,int C,int l,int r,int rt){
    if(L<=l&&r<=R){
        sum[rt]=1<<(C-1);
        flag[rt]=C;
        return ;
    }
    int m=(l+r)>>1;
    push_down(rt);
    if(L<=m)update(L,R,C,lson);
    if(R>m)update(L,R,C,rson);
    push_up(rt);
}

int query(int L,int R,int l,int r,int rt){
    if(L<=l&&r<=R){
        return sum[rt];
    }
    int m=(l+r)>>1;
    push_down(rt);
    int ans=0;
    if(L<=m)ans|=query(L,R,lson);
    if(R>m)ans|=query(L,R,rson);
    return ans;
}

int main(){
    int n,T,O,a,b,c;
    scanf("%d%d%d",&n,&T,&O);
    char s[5];
    build(1,n,1);
    memset(flag,0,sizeof(flag));
    while(O--){
        scanf("%s",s);
        if(s[0]=='C'){
            scanf("%d%d%d",&a,&b,&c);
            if(a>b)swap(a,b);
            update(a,b,c,1,n,1);
        }
        else{
            scanf("%d%d",&a,&b);
            if(a>b)swap(a,b);
            int tmp=query(a,b,1,n,1);
            int res=0;
            while(tmp){
                if(tmp&1)res++;
                tmp>>=1;
            }
            printf("%d\n",res);
        }
    }
}