演算法之貪心學習 --- 兩個案例
阿新 • • 發佈:2018-11-09
貪心演算法
演算法簡介:
- 貪心演算法是指:在每一步的求解的步驟中,他要求"貪婪"的選擇最佳操作,並希望通過一系列的最優選擇,找到一個全域性的最優解。(但有時候是找不到全域性最優);
- 貪心演算法需滿足:
- 可行性:即每一步都必須滿足問題的約束
- 區域性最優 :他是當前步驟中所有可行選擇中最佳的區域性選擇。
- 不可取消: 即選擇一旦做出,在演算法的後面步驟就不可改變。
- 貪心演算法需滿足:
演算法案例:
- 活動選擇問題:
問題描述:有n個需要在同一天使用同一個教室的活動a1,a2,…,an,教室同一時刻只能由一個活動使用。每個活動ai都有一個開始時間si和結束時間fi 。一旦被選擇後,活動ai就佔據半開時間區間[si,fi)。如果[si,fi]和[sj,fj]互不重疊,ai和aj兩個活動就可以被安排在這一天。該問題就是要安排這些活動使得儘量多的活動能不衝突的舉行。例如下圖所示的活動集合S,其中各項活動按照結束時間單調遞增排序
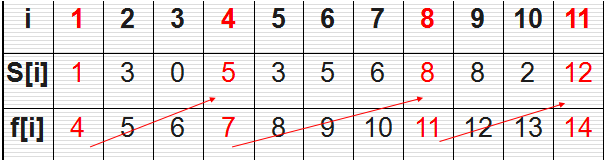
貪心思想:活動越早結束,剩餘的時間越多,那我就選最早結束的那個活動,找到後繼續在剩餘的活動中找最早結束的活動 … …
事實證明貪心演算法在這個問題中可以得到最優解:
實現如下(c++):
#include <iostream> #include <algorithm> using namespace std; struct active { int L; int R; }; bool cmp(active a, active b) { return a.R < b.R; } int main() { int N; cin >> N; int M; // M代表結束時間,可能為0 時,當結束時間為 0 時其實是M時 cin >> M; struct active acts[N]; int ret = 0; for(int i = 0; i < N; i++) { cin >> acts[i].L; cin >> acts[i].R; if(acts[i].R == 0) { acts[i].R = M; } } sort(acts, acts + N -1, cmp); int time_now = 0; for(int i = 0; i < N; i++) { if(time_now <= acts[i].L) { ++ret; time_now = acts[i].R; } } cout<< ret; return 0; }
結果:
實現(java (來自網際網路,我沒有試,不過邏輯正確)):
public class ActiveTime { public static void main(String[] args) { //建立活動並新增到集合中 Active act1 = new Active(1, 4); Active act2 = new Active(3, 5); Active act3 = new Active(0, 6); Active act4 = new Active(5, 7); Active act5 = new Active(3, 8); Active act6 = new Active(5, 9); Active act7 = new Active(6, 10); Active act8 = new Active(8, 11); Active act9 = new Active(8, 12); Active act10 = new Active(2, 13); Active act11 = new Active(12, 14); List<Active> actives = new ArrayList<Active>(); actives.add(act1); actives.add(act2); actives.add(act3); actives.add(act4); actives.add(act5); actives.add(act6); actives.add(act7); actives.add(act8); actives.add(act9); actives.add(act10); actives.add(act11); List<Active> bestActives = getBestActives(actives, 0, 16); for (int i = 0; i < bestActives.size(); i++) { System.out.println(bestActives.get(i)); } } /** * * @param actives * 活動集合 * @param startTime * 教室的開始使用時間 * @param endTime * 教室的結束使用時間 * @return */ public static List<Active> getBestActives(List<Active> actives, int startTime, int endTime) { //最佳活動選擇集合 List<Active> bestActives = new ArrayList<Active>(); //將活動按照最早結束時間排序 actives.sort(null); //nowTime 用來記錄上次活動結束時間 int nowTime = startTime; /** * 因為我們已經按照最早結束時間排序,那麼只要活動在時間範圍內 * actives.get(1)就應當是第一個活動的結束時間. * 則我們記錄第一次活動結束的時間,在結合剩下的活動中, * 選取開始時間大於nowTime且結束時間又在範圍內的活動,則為第二次活動時間, * 知道選出所有活動 */ for (int i = 0; i < actives.size(); i++) { Active act = actives.get(i); if(act.getStartTime()>=nowTime&&act.getEndTime()<=endTime){ bestActives.add(act); nowTime = act.getEndTime(); } } return bestActives; } } /** * 活動類 * @CreatTime 下午9:45:37 * */ class Active implements Comparable<Active>{ private int startTime;//活動開始時間 private int endTime;//活動結束時間 public Active(int startTime, int endTime) { super(); this.startTime = startTime; this.endTime = endTime; } public int getStartTime() { return startTime; } public void setStartTime(int startTime) { this.startTime = startTime; } public int getEndTime() { return endTime; } public void setEndTime(int endTime) { this.endTime = endTime; } @Override public String toString() { return "Active [startTime=" + startTime + ", endTime=" + endTime + "]"; } //活動排序時按照結束時間升序 @Override public int compareTo(Active o) { if(this.endTime>o.getEndTime()){ return 1; }else if(this.endTime == o.endTime){ return 0; }else{ return -1; } } }
- 找零錢問題
問題描述:這個問題在我們的日常生活中就更加普遍了。假設1元、2元、5元、10元、20元、50元、100元的紙幣分別有c0, c1, c2, c3, c4, c5, c6張。現在要用這些錢來支付K元,至少要用多少張紙幣?用貪心演算法的思想,很顯然,每一步儘可能用面值大的紙幣即可。在日常生活中我們自然而然也是這麼做的。
程式碼實現(C++):
#include <iostream>
#include <algorithm>
using namespace std;
int change(int money, int *values, int *counts , int length)
{
int ret[length];
int num = 0;
for (int i = length - 1; i >=0; i--)
{
int cou = min(money/values[i], counts[i]);
cout << cou <<endl;
money = money - cou * values[i];
num += cou;
ret[i] = cou;
}
cout << num << endl;
for (int i=0; i < length; i++)
{
cout << ret[i] << " ";
}
return num;
}
int main()
{
//人民幣面值集合
int values[] = {1,2,5,10,20,50,100};
int counts[] = {3,1,2,1,1,3,5};
int length = sizeof(values) / sizeof(values[0]);
cout << length;
int num = change(442, values, counts, length);
return 0;
}
java程式碼實現:(來自網際網路):
package GreedyAlgorithm;
public class CoinChange {
public static void main(String[] args) {
//人民幣面值集合
int[] values = { 1, 2, 5, 10, 20, 50, 100 };
//各種面值對應數量集合
int[] counts = { 3, 1, 2, 1, 1, 3, 5 };
//求442元人民幣需各種面值多少張
int[] num = change(442, values, counts);
print(num, values);
}
public static int[] change(int money, int[] values, int[] counts) {
//用來記錄需要的各種面值張數
int[] result = new int[values.length];
for (int i = values.length - 1; i >= 0; i--) {
int num = 0;
//需要最大面值人民幣張數
int c = min(money / values[i], counts[i]);
//剩下錢數
money = money - c * values[i];
//將需要最大面值人民幣張數存入陣列
num += c;
result[i] = num;
}
return result;
}
/**
* 返回最小值
*/
private static int min(int i, int j) {
return i > j ? j : i;
}
private static void print(int[] num, int[] values) {
for (int i = 0; i < values.length; i++) {
if (num[i] != 0) {
System.out.println("需要面額為" + values[i] + "的人民幣" + num[i] + "張");
}
}
}
}

總結:於是我們可以看出,有些情況,貪心演算法確實可以給出最優解,然而,還有一些問題並不是這種情況。對於這種情況,我們關心的是近似解,或者只能滿足於近似解,貪心演算法也是有價值的。
ps: 在這裡我想學習這種貪心的策略,就是找到該貪什麼心,這是重點,例如第一題就是貪最早結束的心,第二題就是貪從最大錢開始拼湊的心,我覺得這是重點!
