【時間】2018.10.18

【題目】剪下波的一些知識(附python及matlab實現剪下波變換的程式碼）

概述

    本文是閱讀論文《基於剪下波變換的人臉表情識別》後，對於其中有關剪下波內容的一些筆記。

    剪下波是一種多尺度幾何分析工具，可以看做是對小波變換的一種改進。小波因其多解析度特性而成為表情識別的有效演算法之一。但眾所周知的是，小波變換具有有限的方向選擇性和基函式各向同性。剪下波是2006年提出的一種新的多尺度幾何方法，在影象處理領域已經得到了廣泛應用。

【附】GitHub中剪下波變換的python實現程式碼--

             matlab實現程式碼---百度雲 連結：https://pan.baidu.com/s/1LbB8nanqW-MBOxajOf4XvA

             提取碼：1rvw

1.1  剪下波的定義及離散演算法

      Shearlet【48】是一類新的多尺度幾何分析方法,該方法通過對基本函式的縮放、剪下和平移等仿射變換來構造，體現了函式的幾何和數學特性，如近幾年來許多領域的研究學者所強調的函式的方向性、尺度和振盪等。Shearlet 可以和多解析度分析關聯起來，這樣就可以獲得像小波-樣的迭代演算法，並推廣到經典的級聯演算法(49。因此Shearlet變換作為一種新型的多尺度幾何分析工具為影象處理領域的研究人員所廣泛接受。

 1.1.1  Shear let變換的定義和性質

   連續剪下波變換解決了波前集問題，其平移引數可檢測到所有奇異點的位置，而剪下引數則可顯示出奇異曲線的方向。

1.1.2.ShearIet變換的離散化

1.2離散可分離剪下波變換及其數值計算

1.2.1 離散可分離剪下波變換(DSST)

    Wang．Q Lim[481在2010年提出了離散可分離剪下波變換(Discrete Shearlet Transform，DSST).

    離散可分離剪下波變換(DSST)的計算方法可通過如下步驟表示：

1.3影象的剪下波分解

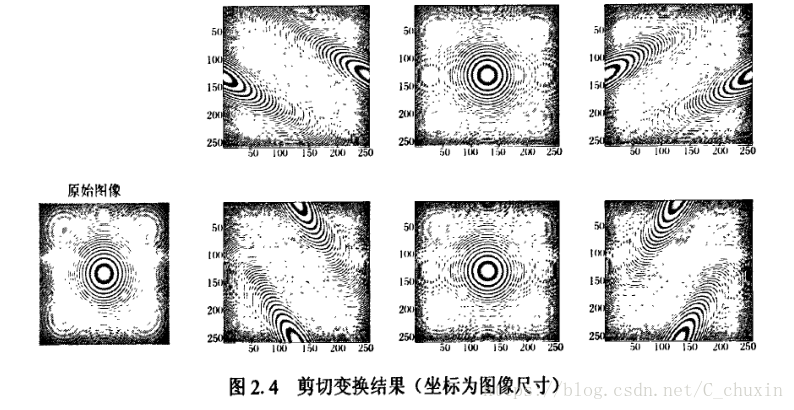
          離散剪下變換通過剪下矩陣將原始影象對映到不同的方向上。方向性的實現通常有兩種方法：旋轉和剪下。在某種意義上，旋轉是一個非常方便的工具，它保留了重要的幾何資訊，如長度、角度和並行性。然而，這種方法不保留整數格，對於數字化有一定的困難。與此相反，剪下矩陣最不但能夠提供方向性，當剪下引數k是整數時，還保留了整數格。圖2．4顯示了一副標準影象“zoneplate"(256X256)經過剪下變換後的結果，有L=6個方向。

     在圖2．4中，上行為在水平錐cn內的三個方向，下行為在垂直錐cl內的三個方向。輸入原始影象尺寸為256×256，由圖可知剪下變換後各個方向分量尺寸仍為256×256。由圖2．4可以看出，剪下波具有很強的方向敏感性。

    各向異性小波變換將影象分解為低頻子帶和高頻子帶。在各向異性小波變換中，沿水平和垂直方向的變換個數是不相等的，也就是說在同一尺度上，沿水平方向上的變換，l-和垂直方向上的變換％並不需要相等【49】。

  將剪下變換得到的各方向子帶進行各向異性離散小波變換完成多解析度分解，即實現剪下波變換。圖2．6顯示了標準影象“zoneplate’’經過三尺度6方向剪下波變換後的剪下波係數。

1.4 ShearIet域的影象特徵分析

1.4.1 影象在Shear Iet域的能量分佈

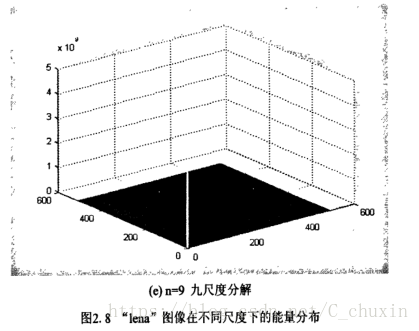
     影象經過某種離散變換後的能量分佈體現了影象的變換特徵，從無失真壓縮的角度考慮，變換的目的是希望影象經離散變換後能量儘可能的集中在少量的幾個係數中，即具有能量聚集性，由此可得到較高的壓縮比。影象經過Shearlet變換後，能量的分佈會隨著變換尺度n的變化呈現出一定的規律。本節通過模擬分析了影象在Shearlet域的能量分佈。為了體現結論的普遍性，模擬影象選用標準“lena’’(512X512)灰度影象，如圖(2．7)所示，並給出了其在Shearlet域能量峰值最分解尺度變化的曲線。圖2．8(a)--2．8(e)給出了“lena’’影象在分解尺度n=l，3，5，7，9時的Shearlet係數的能量分佈。

從圖2．8(a)～(e)可以清楚的看出：對於的影象，對其進行11尺度二維離散Shearlet變換時，能量主要集中在的區

域內，即低頻分量部分；隨著分解尺度的增大，影象在Shearlet域的能量分佈趨於二維座標平面的原點。此對於的影象，Shearlet變換的係數為

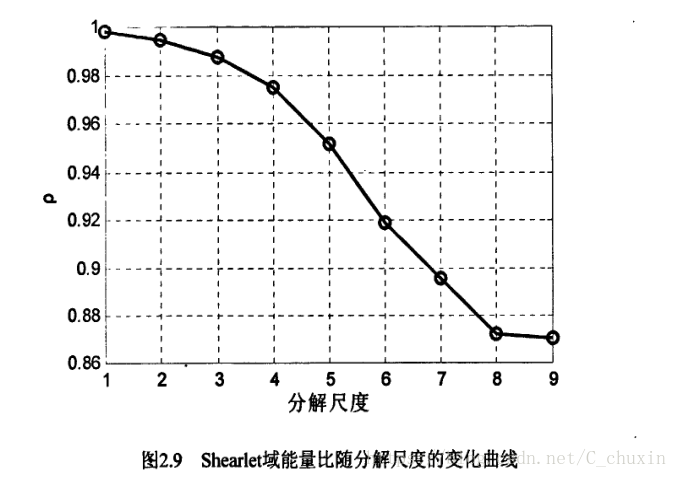
，定義能量比p為:

  圖2.9分別給出了“lena”影象的Shearlet域能量比值P隨尺度變化的過程。由圖2．9可以看出，隨著分解尺度的增大，低頻區域包含的總能量卻在慢慢減少，儘管如此，在六尺度Shearlet分解時，Shearlet域的能量在此區域內的聚焦度依然達到了90％以上。由以上分析可知，影象的Shearlet變換具有良好的聚焦性。所以當我們利用Shearlct變換提取表情特徵時，低頻分量應該作為識別的重要特徵。

1.4.2影象在ShearIet域的低頻與高頻特徵

(1)由圖2．10(a)～圖2．14(a)可以看出，Shearlet變換後的低頻分量主要體現了影象的輪廓資訊。在表情識別中，體現的主要是表情的概貌。當分解尺度由小變大時，低頻分量含有的資訊越來越少，僅由低頻部分重構的影象越來越模糊。當分解尺度較少時，相當於經歷了截止頻率較高的低通濾波器，高頻成分浮現出來，還能清晰的看到影象的邊緣，如圖2．10(a)所示。分解尺度較大時，相當於截止頻率較低的低通濾波器，如圖2．14(a)所示。

(2)由圖2．10(b)～圖2．14(b)可以看出，由高頻部分重構的影象可以很明顯的觀察到“lena"的邊緣資訊。影象的邊緣和紋理資訊主要包含在含有高頻部分的資訊中，隨著分解尺度的增大，邊緣和紋理資訊越來越明顯，而在表情識別中，人臉面部的邊緣和紋理資訊在識別過程中發揮著重要的作用。當對影象進行完全分解時，對應於截止頻率非常低的高通濾波器，只有小部分低頻分量被濾除出，僅由高頻資訊重構的影象接近原影象，如圖2．14(b)所示。

(3)當分解尺度適中時，由低頻和高頻所重構的影象均既包含了原影象的輪廓資訊，也包含了原影象的邊緣資訊，如圖2．1l(a)和2．12(b)所示，這對於表情識別是非常重要的。

1.4.3影象在ShearIet域的各尺度高頻特徵

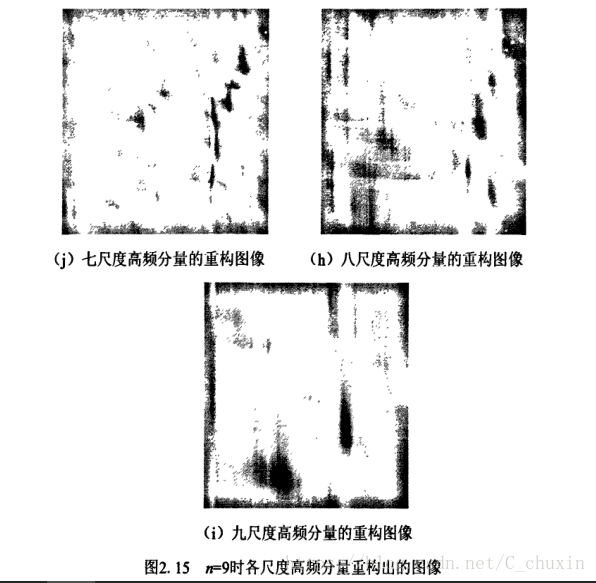
    高頻部分主要體現了影象的邊緣和紋理資訊，那麼對於刀尺度Shearlet變換來說，研究各尺度高頻分量之間的有何區別，又有何相關的性質的有必要的。對影象進行完全分解，分別使用各尺度高頻係數做二維離散Shearlet反變換，得到分別由各尺度高頻Shearlet係數重構出的影象。

    選用“lena’’(512X512)影象進行模擬，在完全分解尺度，腳下的模擬結果如圖2．15(a)～(i)所示，方向數目均為6。

    由圖2．15(a)～(i)可以看出，隨著尺度的逐漸增大，影象在Shearlct域的各尺度高頻資訊經過逆變換所得到的影象的邊緣經歷了一個由模糊到清晰再到模糊的過程，圖2．15(b)～(d)重構邊緣效果比較好，而且在圖2．15(g)一(i)中，邊緣資訊越來越模糊。因此在本文的識別系統中，並不將表情影象的Shearlet係數全部用做特徵，而考慮將低頻分量與某一尺度體現邊緣效果好的高頻分量融合作為表情特徵進行提取。