GAIL生成對抗模仿學習詳解《Generative adversarial imitation learning》
前文是一些針對IRL,IL綜述性的解釋,後文是針對《Generative adversarial imitation learning》文章的理解及公式的推導。
- 通過深度強化學習,我們能夠讓機器人針對一個任務實現從0到1的學習,但是需要我們定義出reward函式,在很多複雜任務,例如無人駕駛中,很難根據狀態特徵來建立一個科學合理的reward。
- 人類學習新東西有一個重要的方法就是模仿學習,通過觀察別人的動作來模仿學習,不需要知道任務的reward函式。模仿學習就是希望機器能夠通過觀察模仿專家的行為來進行學習。
- OpenAI,DeepMind,Google Brain目前都在向這方面發展。
[1] Model-Free Imitation Learning with Policy Optimization, OpenAI, 2016
[2] Generative Adversarial Imitation Learning, OpenAI, 2016
[3] One-Shot Imitation Learning, OpenAI, 2017
[4] Third-Person Imitation Learning, OpenAI, 2017
[5] Learning human behaviors from motion capture by adversarial imitation, DeepMind, 2017
[6] Robust Imitation of Diverse Behaviors, DeepMind, 2017
[7] Unsupervised Perceptual Rewards for Imitation Learning, Google Brain, 2017
[8] Time-Contrastive Networks: Self-Supervised Learning from Multi-View Observation, Google Brain, 2017
[9] Imitation from Observation/ Learning to Imitate Behaviors from Raw Video via Context Translation, OpenAI, 2017
[10] One Shot Visual Imitation Learning, OpenAI, 2017
模仿學習
- 從給定的專家軌跡中進行學習。
- 機器在學習過程中能夠跟環境互動,到那時不能直接獲得reward。
- 在任務中很難定義合理的reward(自動駕駛中撞人reward,撞車reward,紅綠燈reward),人工定義的reward可能會導致失控行為(讓agent考試,目標為考100分,但是reward可能通過作弊的方式)。
- 三種方法:
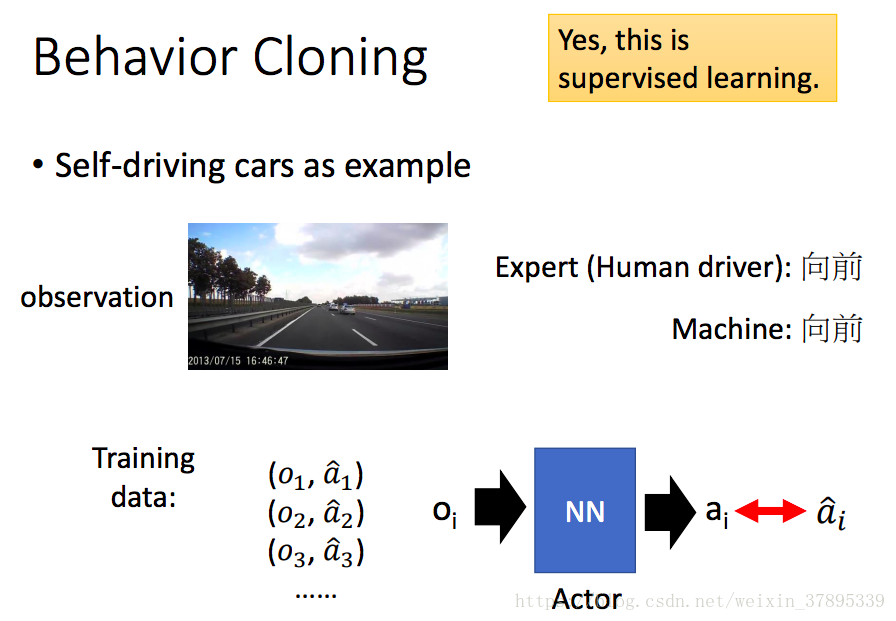
a. 行為克隆(Behavior Cloning)
b. 逆向強化學習(Inverse Reinforcement Learning)
c. GAN引入IL(Generative Adversarial Imitation Learning) - 行為克隆
有監督的學習,通過大量資料,學習一個狀態s到動作a的對映。
但是專家軌跡給定的資料集是有限的,無法覆蓋所有可能的情況。如果更換資料集可能效果會不好。則只能不斷增加訓練資料集,儘量覆蓋所有可能發生的狀態。但是並不實際,在很多危險狀態採集資料成本非常高。 - 逆向強化學習
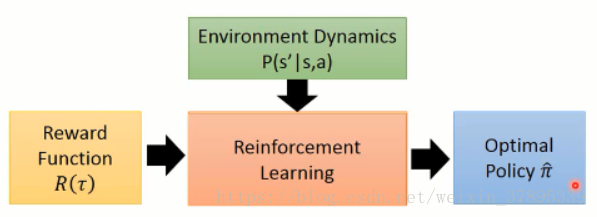
RL是通過agent不斷與environment互動獲取reward來進行策略的調整,最終得到一個optimal policy。但IRL計算量較大,在每一個內迴圈中都跑了一遍RL演算法。
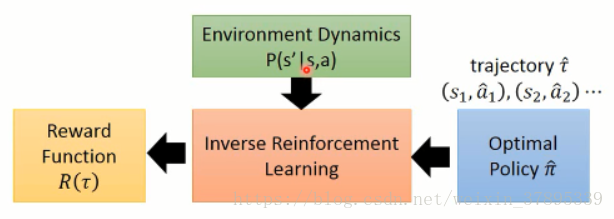
IRL不同之處在於,無法獲取真實的reward函式,但是具有根據專家策略得到的一系列軌跡。假設專家策略是真實reward函式下的最優策略,IRL學習專家軌跡,反推出reward函式。
得到復原的reward函式後,再進行策略函式的估計。
RL演算法:
IRL演算法:
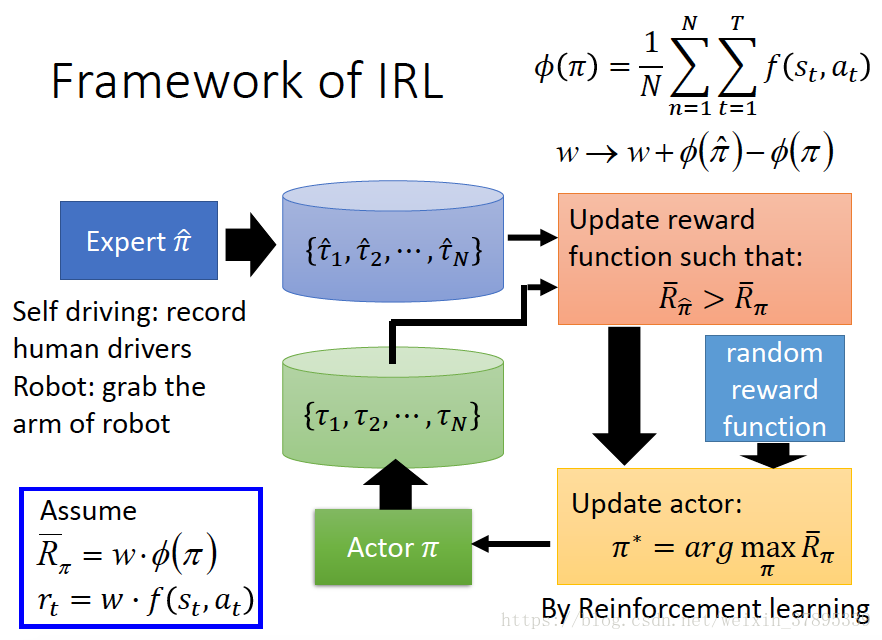
在給定的專家策略後(expert policy),不斷尋找reward function來使專家策略是最優的。(解釋專家行為,explaining expert behaviors)。具體流程圖如下:
- 生成對抗模仿學習(GAN for Imitation Learning)
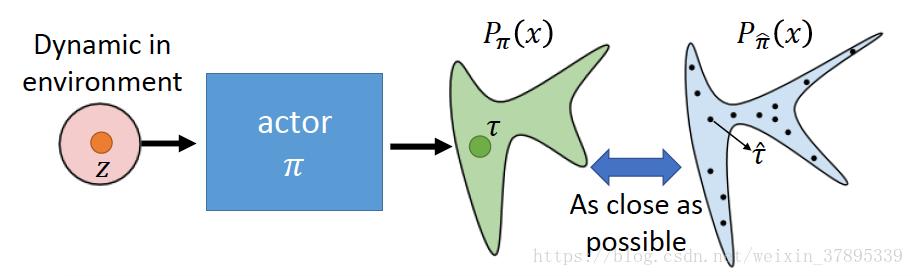
我們可以假設專家軌跡是屬於某一分佈(distribution),我們想讓我們的模型也去預測一個分佈,並且使這兩個分佈儘可能的接近。
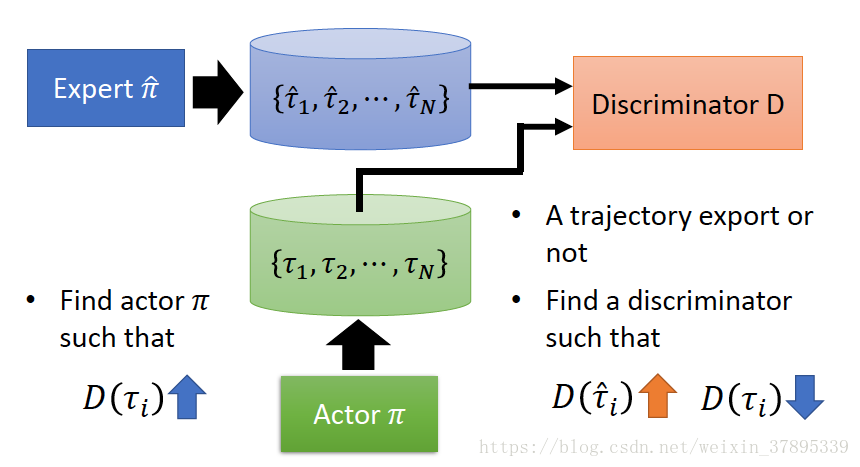
演算法流程如下:
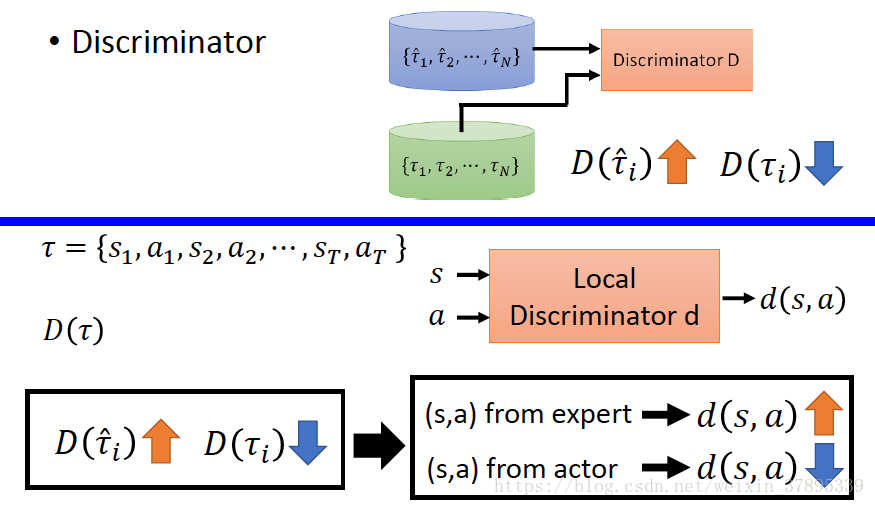
Discriminator:儘可能的區分軌跡是由expert生成還是Generator生成。
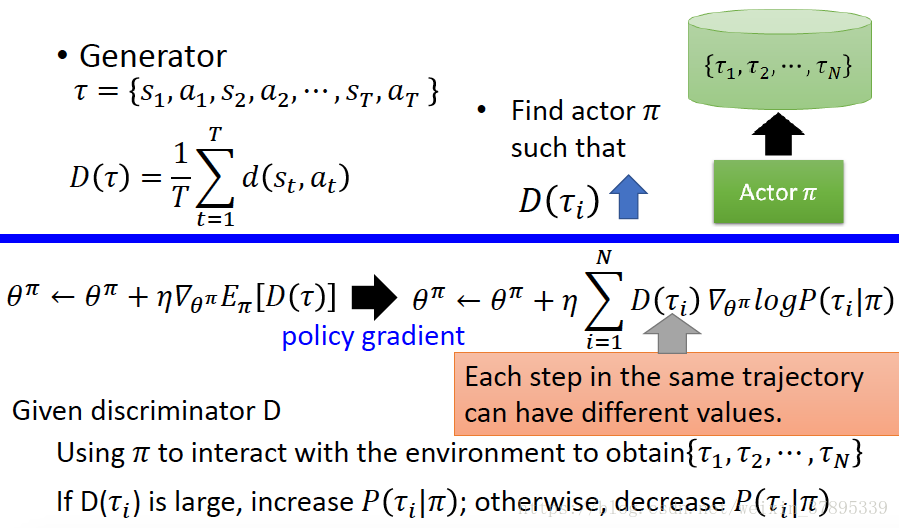
Generator(Actor):產生出一個軌跡,使其與專家軌跡儘可能相近,使Discriminator無法區分軌跡是expert生成的還是Generator生成的。
其演算法可以寫為:
生成對抗模仿學習(Generative Adversarial Imitation Learning)
GAIL能夠直接從專家軌跡中學得策略,繞過很多IRL的中間步驟。
逆向強化學習(IRL)
假定cost function的集合為
,
為專家策略。帶有正則化項
最大熵逆向強化學習是想找到一個cost function似的專家策略的效果優於其餘所有策略(cost越小越優):
其中
,
是一個
折扣累積熵。IRL過程中包含一個RL過程:
Defination 1.
對於一個策略
,定義其佔用率度量(occupancy measure)
為
佔用率度量可以近似看做是使用策略
時,狀態-動作對的分佈。
是有效的佔用率度量的集合。
[1] U. Syed, M. Bowling, and R. E. Schapire. Apprenticeship learning using linear programming. In
Proceedings of the 25th International Conference on Machine Learning, pages 1032–1039, 2008. 證明
與
是一一對應關係。
Lemma 3.1.
若 ,則 是策略 的佔用率度量,並且 是唯一的。
根據Definition 1,可以將
折累計代價寫為
Lemma 3.2.
若 ,