目錄

• 中國市場上的利率互換估值
  • 1. 導論
  • 2. 定價模型
    • 2.1. 雙曲線貼現
    • 2.2. 單曲線貼現
    • 2.3. 估值差異
  • 3. 中國互換市場中無風險利率的候選項
  • 4. 數值測試
  • 5. 結論
  • 參考文獻

中國市場上的利率互換估值

本文翻譯自《Interest Rate Swap Valuation in the Chinese Market》

作者：Wei Cui、Min Dai、Steven Kou、Yaquan Zhang、Chengxi Zhang、Xianhao Zhu

機構：Risk Management Institute，National University of Singapore

成文時間：December 8, 2017

在 2008 年金融危機之後，雙曲線貼現法被廣泛用於以主要貨幣計價的利率互換估值，這意味著市場一致接受隔夜互換利率作為無風險利率的新代表。然而，在中國市場，過時的單曲線貼現法仍然被廣泛使用，因為對代表無風險利率的選擇沒有達成共識。我們將雙曲線貼現法應用於中國利率互換市場，並建議使用中國回購市場的基準利率 7 天回購定盤利率作為無風險利率。根據經驗，對於固定利率接收方，使用單曲線貼現方法可能會顯著低估互換合約。

關鍵詞：Multi-curve models; Short rate models; Pricing of interest rate swaps; The Chinese market; Risk-free rate; Repo rate.

1. 導論

在金融市場中，利率互換一直被用作投資和風險管理的工具。最常見的型別是“普通香草”利率互換。在此互換中，一方定期支付由固定互換利率確定的現金流，並接收由基準浮動利率確定的現金流。這是中國市場上唯一一種利率互換交易，也是本文的重點。（譯註：至少原文寫作時期是這樣的。）

利率互換的定價在不同背景下具有不同的含義。在市場上，只有新合約才被經常交易。這些合約以固定互換利率報價，使合約在初始時期的價值為零。因此，為新的利率互換合約定價意味著確定互換利率。另一種情況是為已知互換利率的現有互換合約定價。在這種情況下，定價通常意味著計算其淨現值，這對會計、風險管理或提前終止合約很重要。在本文中，互換估值等式用於第二種情況。但是，可以通過重新安排合約條款輕鬆地修改它們，以獲得新合約的互換利率。

擁有合適的互換估值等式的好處不僅限於正確計算互換價格。通常情況下，利率（例如 Libor 或 Shibor）僅在短期限內（最多 1 年）報價，而其互換可能具有更長的期限。因此，市場參與者依靠互換利率來推導長期利率期限結構。這種技術稱為自舉法，它是互換合約估值等式的逆過程。因此，合適的估值等式對於市場正確推導期限結構至關重要。

國際上，在 2008 年金融危機之前，為了定價利率互換，行業慣例是將 Xibor 利率¹視為無風險利率，並使用利率本身來預測和貼現 Xibor 互換現金流。由於此過程僅涉及 Xibor 曲線，因此此估值方法稱為單曲線貼現法。

但是，Xibor 利率並非真正無風險。這是金融機構之間無擔保的貸款利率。例如，Collin-Dufresne 和 Solnik [1] 認為 Libor 與 AA 評級的金融機構具有相同的信用風險。在 2008 年金融危機之前，Xibor 中嵌入的風險在實踐中並不顯著，Xibor 與隔夜互換（OIS）²曲線之間的差距很小。在 2008 年金融危機之後，如圖 1 所示，這些利差變得越來越重要。Hull 和 White [2] 指出利差反映了銀行對彼此的信用擔憂。這種現象使得用 Xibor 曲線貼現現金流的做法存在問題。

為了解釋 Xibor 中嵌入的風險，從業者已經轉而使用稱為雙曲線貼現的新估值方法。在此框架下，在 Xibor 互換的估值中，選擇另一種無風險利率曲線用於貼現現金流。由於無風險利率曲線的選擇通常是主要貨幣的 OIS 利率，因此這種方法也被稱為 OIS 貼現，Grbac 和 Runggaldier [3] 以及許多其他人均有記述。

中國在岸市場的利率互換場外交易始於 2006。在過去十年中，中國互換市場取得了長足的進步。2016 年，互換交易超過 87,000 筆，名義價值為 9.9 萬億人民幣。流行的基準浮動利率是 7 天銀行間回購定盤利率（7D 回購利率），佔市場份額的 86%，以及 3 個月的 Shibor（3M Shibor），佔市場份額的 11%。

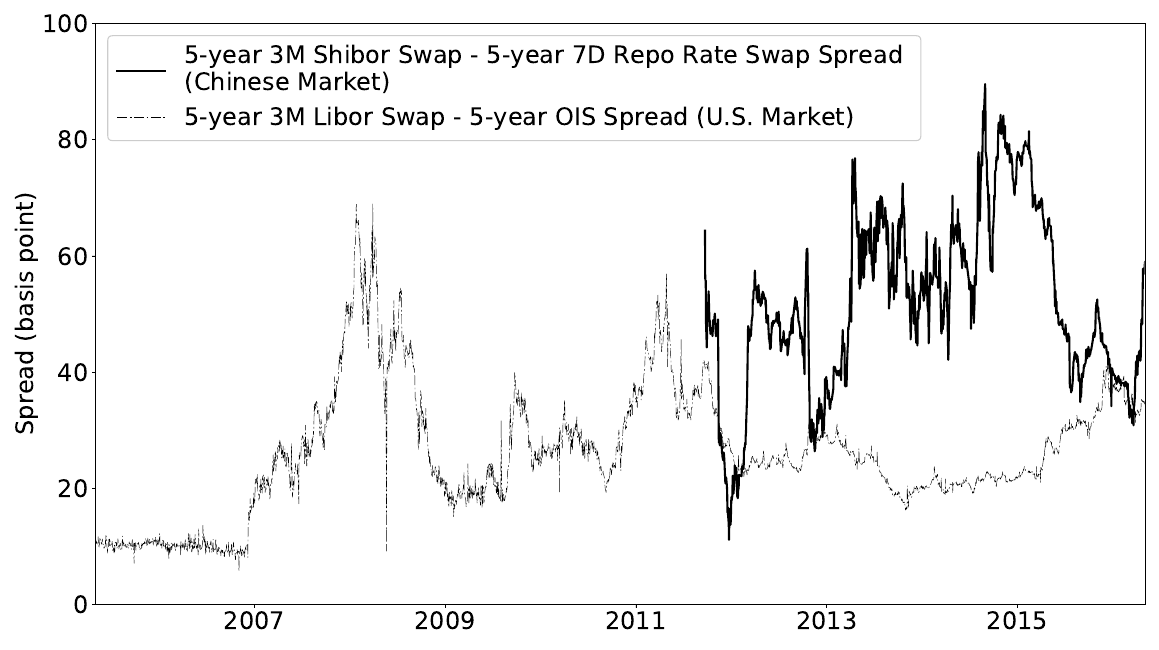
圖 1 顯示了 3M Shibor 與中國市場 7D 回購利率之間的利差。這種利差比在美國市場觀察到的風險和無風險利率之間的利差更為顯著。合理地定價互換合約需要考慮這種利差。

儘管市場規模迅速增長，但中國市場使用的估值方法仍然落後。市場參與者仍然使用單曲線方法基於風險浮動利率對互換進行定價。以下是在中國市場使用單曲線方法的一些例子。（譯註：至少原文寫作時期是這樣的。）

1. 中國外匯交易中心（CFETS）是一個組織和監管中國利率互換市場的政府機構。它每天在其網站³上報告一些基準浮動利率的遠期利率。這些遠期利率是通過使用單曲線方法推導市場互換利率而獲得的。
2. 除了報告遠期利率外，CFETS 還提供互換合約的雙邊提前終止服務。在此服務中，CFETS 使用單曲線方法計算要終止的合約的價值。
3. 彭博通過其終端提供利率互換估值服務。它提供一系列主要貨幣的雙曲線貼現，包括美元和歐元，但不包括人民幣。以人民幣計價的互換，彭博估值使用單曲線法推匯出遠期利率。

圖 1 虛線顯示了 3M Libor 的 5 年期互換利率與美國市場 5 年期 OIS 利率之間的利差。實線顯示 3M Shibor 的 5 年期互換利率與中國市場的 7D 回購利率之間的利差。中國市場的歷史互換利率資料始於 2012 年中期。

本文的貢獻是雙重的。首先，我們比較中國市場的幾個利率。我們建議使用 7D 回購利率作為互換估值的無風險利率。其次，我們測試了中國市場的雙曲線貼現方法。我們的結果顯示，對固定利率接收方來說，目前的單曲線貼現法可能會顯著低估互換合約。

本文的其餘部分安排如下。第 2 節重新審視了利率互換的建模框架和估值等式，並在數學上分析了估值方法的變化如何影響估值結果。第 3 節討論了中國互換市場中無風險利率的選擇。在第 4 節，使用來自中國市場的資料，我們分別使用單曲線和雙曲線貼現法對 Shibor 互換合約進行定價，並分析估值差異。最後，我們在第 5 節中得出結論。

2. 定價模型

2.1. 雙曲線貼現

為了後續分析的完整性，我們首先介紹數學符號並回顧利率互換的定價等式。有大量文獻討論危機後的利率模型。一些例子是 Ametrano 和 Bianchetti [4]、Filipovic 和 Trolle [5] 以及 Grbac 和 Runggaldier [3]。儘管他們的結果非常相似，但他們的術語和中間步驟有微妙的差異。在本文中，我們通常遵循 Grbac 和 Runggaldier [3] 的邏輯，因為它與危機前的單曲線情形相似。

雙曲線建模框架從無風險零息債券的價格開始，記為 \(D_{rf}(t,T)\)⁴。時間 \(t\) 處的無風險零息債券曲線指的是函式 \(T \to D_{rf}(t,T)\)。對應於零息債券，我們將連續複利的無風險瞬時遠期利率定義為 \(f_{rf}(t,T):= - \partial_T \ log D_{rf}(t,T)\)，並定義 \(r_{rf}(t)= f_{rf}(t,t)\) 為連續複利無風險短期利率。

設 \(Q\) 代表風險中性測度，其中計價單位是貨幣市場賬戶 \(B_{rf}(0, T)= \exp \left(\int_0^1 r_{rf}(u)du \right)\)。在這一測度下，應用資產定價基本定理的直接結果是無風險債券價格為 \(D_{rf}(t,T)= E^Q \left [\exp \left \{ - \int_t^T r_{rf}(u)du \right \} | F_t \right]\)。我們使用 \(D_{rf}(t,T)\) 作為計價單位進一步定義了遠期測度 \(Q^T\)。

在市場上，（至少）有兩個簡單的利率。用 \(R_{rf}(t_i,t_j)\) 表示無風險利率，以及 \(R_{risky}(t_i,t_j)\) 表示風險利率⁵。兩種利率都是固定的，並在 \(t_i\) 生效，在 \(t_j\) 到期。然後 \(R_{rf}(t_i,t_j)\) 是區間 \([t_i,t_j]\) 上的單利，即在 \(t_i\) 投資購買 \(t_j\) 到期的無風險債券，數學表示，

\[ R_{rf}(t_i,t_j)=\left(\frac{1}{D_{rf}(t_i,t_j)} -1 \right) \frac{1}{t_j -t_i}. \]

當期限不重要時，我們只是使用 \(R_{rf}\) 和 \(R_{risky}\) 來指代利率。

我們將 \(R_{rf}\) 和 \(R_{risky}\) 在 \(t < t_i\) 的離散複利遠期利率分別表示為 \(F_{rf}(t; t_i,t_j)\) 和 \(F_{risky}(t;t_i,t_j)\)。在本文的其餘部分，它們被稱為遠期利率。遵循 Grbac 和 Runggaldier [3]，它們被定義如下：

\[ F_{rf} (t; t_i , t_j) := E^{Q^{t_j}}[R_{rf} (t_i , t_j)|F_t] \\ F_{risky} (t; t_i , t_j) := E^{Q^{t_j}}[R_{risky} (t_i , t_j)|F_t]. \]

我們將 \(t_{0 \le i \le n}\) 表示付款時間表，其中 \(t_i = t_{i-1} + \Delta\)，\(t_0\) 是開始日期，\(\Delta\) 是固定長度的時間間隔⁶。雙曲線利率互換估值等式可以在 Grbac 和 Runggaldier [3]⁷中找到。更確切地說，我們將浮動利率 \(R_{rf}\) 或 \(R_{risky}\) 上的利率互換分別稱為 \(R_{rf}\) 互換或 \(R_{risky}\) 互換。在 \(t \le t_1\) 時，固定利率接收方的 \(R_{rf}\) 互換和 \(R_{risky}\) 互換的價格如下：

\[ V_{rf}(t) = N\sum_{i=0}^{n-1}D_{rf}(t,t_{i+1})\Delta[s_{rf}-F_{rf}(t;t_i,t_{i+1})], \]

\[ V_{risky}(t) = N\sum_{i=0}^{n-1}D_{rf}(t,t_{i+1})\Delta[s_{risky}-F_{risky}(t;t_i,t_{i+1})]. \tag{1} \]

其中 \(N\) 是名義金額，\(s_{rf}\) 和 \(s_{risky}\) 是各自的互換利率。

使用等式（1）估算 \(R_{risky}\) 互換，需要用 \(R_{rf}\) 的利率曲線來校準貼現因子 \(D_{rf}\)，並按 \(R_{risky}\) 的利率曲線校準遠期利率。由於此方法涉及兩條曲線，因此將其命名為雙曲線貼現。

然而，很少有長期限單利直接在市場上報價。例如，Libor 和 Shibor 的最長期限為 1 年。為了獲得整個利率曲線，市場慣例是使用稱為自舉（譯註：bootstraping）的方法，這實質上是互換估值等式的逆過程。此方法的輸入是一系列市場互換利率。長期限的標準化互換合約在市場上經常交易。該方法的輸出是貼現因子或遠期利率的曲線，然後可用於估值非標準或現有的互換合約。讀者可以參考 Ametrano 和 Bianchetti [4] 進行詳細實現。請注意，除了互換利率之外，Ametrano 和 Bianchetti [4] 中的自舉過程也使用期貨合約作為輸入。由於中國市場沒有 Shibor 的期貨，我們在實現中僅使用互換利率。

在上面的推導中，我們故意忽略由天數計算規則產生的細微差別，以保持表示符號的清晰。但是，在實現中，我們應該考慮它們以產生正確的數值結果。有關天數計算規則的更多詳細資訊，請參閱 Henrard [7]。（譯註：或者這裡）

2.2. 單曲線貼現

如引言中所述，在當前的中國市場中，單曲線貼現法仍然存在於互換定價中。為了分析這兩種方法的數值差異，我們簡要介紹單曲線方法。

單曲線和雙曲線貼現法之間的區別在於 \(R_{risky}\) 互換的估值。在單曲線建模框架下，儘管存在風險，但 \(R_{risky}\) 也被視為無風險。估值等式由下式給出：

\[ V_{risky}(t) = N\sum_{i=0}^{n-1}D_{risky}(t,t_{i+1})\Delta[s_{risky}-F_{risky}(t;t_i,t_{i+1})]. \tag{2} \]

其中 \(D_{risky}(t,t_{i + 1})\) 是在 \(R_{risky}\) 是無風險的錯誤假設下計算的貼現因子。有關單曲線估值等式的推導，請參閱 Brigo 和 Mercurio [8]。

如果兩個利率曲線接近，則在實踐中使用 \(R_{rf}\) 和 \(R_{risky}\) 作為無風險利率是可以接受的。然而，如圖 1 所示，在中國市場，7D 回購利率與 3M Shibor 之間存在巨大差異。因此，單曲線方法顯然存在問題。

最後，類似於雙曲線的情況，實現等式（2），首先需要以 \(R_{risky}\) 互換的互換利率作為輸入執行自舉。人們仍然可以參考 Ametrano 和 Bianchetti [4]，瞭解如何在單曲線方法下執行自舉。請注意，自舉方法依賴於互換估值等式。因此，在與輸入相同的互換利率下，更改估值等式會導致不同的貼現因子、遠期利率和估值結果。

2.3. 估值差異

在這一部分中，我們分析了在估值 \(R_{risky}\) 互換時從單曲線方法切換到雙曲線方法所產生的估值差異。我們嘗試憑經驗確定這種估值差異的驅動因素。

假設我們最初從固定利率接收方進入 \(R_{risky}\) 互換合約。我們用 \(s^{fix}_{risky}\) 表示這個合約的固定利率，用 \(V_{risky}\) 表示它的價值。一段時間後，我們進入一份新的合約作為固定利率支付方，其基準浮動利率與之前的相同。新合同旨在與前一個合同具有相同的到期日、付款日期和名義本金。因此，兩個合約浮動端產生的未來現金流量將相互抵消。假設這個新合約是在時間 \(t\) 時進入的，互換利率為 \(s^{par}_{risky}\)，使得合約的價值在 \(t\) 時為零。請注意，這份新合約的互換利率恰好是舊合約在 \(t\) 的平價利率。進一步假設 \(s^{fix}_{risky}\) 和 \(s^{par}_{risky}\) 均來自流動好的市場，因此這些值與我們選擇的估值方法無關。

考慮由兩個互換組成的投資組合的價值。注意第二個合約在 \(t\) 處的價值為零。因此，投資組合的價值與舊互換的價值相同。同樣，這兩個互換的浮動端產生的現金流被抵消。雙曲線和單曲線貼現法下的 \(R_{risky}\) 互換的值分別由下式給出：

\[ V_{risky}^{dual}(t) = V_{risky}^{dual}(t) + 0 = N \sum_{i=0}^{n-1}(s^{fix}_{risky}-s^{par}_{risky})D_{rf}(t,t_{i+1})\Delta,\\ V_{risky}^{single}(t) = V_{risky}^{single}(t) + 0 = N \sum_{i=0}^{n-1}(s^{fix}_{risky}-s^{par}_{risky})D_{risky}(t,t_{i+1})\Delta, \]

其中 \(V_{risky}^{dual}(T)\) 和 \(V_{risky}^{single}(T)\) 代表從雙曲線和單曲線方法得出的估值。取兩者的差，然後由轉換估值方法得出的估值變化是

\[ V_{risky}^{dual}(t) - V_{risky}^{single}(t) = N \sum_{i=0}^{n-1}(D_{rf}(t,t_{i+1}) - D_{risky}(t,t_{i+1}))(s^{fix}_{risky}-s^{par}_{risky})\Delta. \]

受益於這個等式，我們不需要在後面的分析中處理無法追蹤的遠期利率。現在很明顯，估值差異有兩個驅動因素，即兩種方法中使用的貼現因子的差異，以及估值時規定的互換利率與平價利率之間的差額。

貼現因子造成的差異由估值日的風險浮動利率與無風險利率之間的差額確定。通常，這種差異是正的。這非常直觀，\(D_{risky}\) 是從風險利率中獲得的，其中隱含但錯誤的假設是利率是無風險的。市場要求承擔風險的溢價，相應的貼現因子較小。

我們從兩個方面分析 \((s^{fix}_{risky} - s_{risky}^{par})\)。首先，市場中互換利率的期限結構通常是向上傾斜的，即期限較長的互換利率大於期限較短的利率。請注意，平價利率實際上是短期限的新互換的互換利率。如果利率市場保持穩定，則規定的固定利率將大於估值時的平價利率。對於在估值時間之前很久簽署的合同，尤其如此。其次，差異將受到市場波動的影響。請注意，平價利率由估值時的市場狀況決定。特別是，如果在簽訂互換合約後市場利率持續上升，第一方面的影響將被抵消，估值差異將不大。相反，如果市場利率向下移動，互換利率與平價利率之間的差異將相應增大。在大多數情況下，\((s^{fix}_{risky} - s_{risky}^{par})\) 是正的，並且觀察到大到 100 個基點的差異並不罕見。

總之，在大多數情況下，使用單曲線方法往往會低估固定利率接收方的利率互換合約。特別是，對於仍然有很長時間到期的合約，以及在合約開始後市場利率不斷下降的情況下，估值偏差最為顯著。在後面的章節中使用市場資料證明了這一論點。但是，我們必須強調，上述分析是經驗性的。實際差異在很大程度上取決於市場條件。

3. 中國互換市場中無風險利率的候選項

在估值理論中，無風險利率是一個重要的組成部分。然而，在金融市場中，幾乎沒有完全無風險的利率。所有從業者都可以做的是比較市場上可用的候選項，並選擇不利性最小的候選項。例如，為了證明 OIS 利率在美國市場的有效性，Hull 和 White [2] 將其與 Libor、國債利率和回購利率進行了比較。在這裡，我們將進行相同的討論，將 7D 回購利率與中國政府債券利率和中國市場的其他利率進行比較。一些論點是從美國市場借鑑來的。

中國政府債券利率：中國政府債券經常在中國在岸市場交易。這些債券得到中國政府的背書，是中國最安全的投資。最受認可的政府債券利率曲線由中央國債登記結算有限責任公司（CCDC）釋出，這是一個政府機構。利率曲線每日使用市場價格計算，期限長達 50 年。利率曲線資料集可在 CCDC 網站上獲得⁸。我們將 \(t\) 時期開始，期限為 \(t + \delta\) 的利率表示 \(Y(t,t+\delta)\)。如果政府利率是無風險利率的代表，則相應的零息債券價格由下式給出

\[ D_{bond}(t,t+\delta)=\frac{1}{(1+Y(t,t+\delta))^\delta},\tag{3} \]

中國政府債券利率與美國國債利率有類似的弊端。首先，政府債券的票息支付是免稅的。這種稅收優惠使得政府債券收益被人為地壓低。其次，政府債券通常用作回購交易的抵押品。這種額外需求也降低了利率。請注意，這些也是美國市場不使用美國國債利率作為無風險利率的原因，見 Hull [9]。如果將政府債券利率用作無風險利率的代表，則產生的貼現因子將人為地放大。因此，政府債券利率可能不是無風險利率的良好代表。

7D 回購利率：2016年，中國回購市場回購交易的總名義價值為 831 萬億元人民幣，約為債券交易總額的 6 倍。在所有期限中，隔夜回購合約是最具流動性的，其次是 7 天回購合約。作為回購市場的基準利率，銀行間回購定盤利率由 CFETS 每個交易日計算和公佈。由於回購交易總是需要抵押品，回購利率似乎是無風險利率的良好代表。

當然，7D 回購利率仍然不是一個完美的選擇。首先，Hull 和 White [2] 觀察到美國市場的回購利率具有很大的橫截面變化：由美國國債擔保的回購利率低於其他債務擔保的回購利率。雖然到目前為止中國市場還沒有關於這種觀察的報道，但我們不應該完全忽視這個問題。另一個潛在的問題是流動性。7 天回購交易並不像隔夜交易那樣具有流動性，這可能是無風險利率的更好代表。然而，在目前的市場中，隔夜回購利率沒有利率互換，也沒有辦法確定一個完整的期限結構。（譯註：至少原文寫作時期是這樣的。）

其他候選項：作為隔夜利率，隔夜 Shibor 乍一看似乎是無風險利率的良好代表。在中國市場也有隔夜 Shibor 互換交易。然而，隔夜 Shibor 互換交易量非常有限：它們佔市場份額不到 3%。因此，所得的互換曲線不被充分的市場資訊所支援。此外，隔夜 Shibor 互換的最長期限僅為 3 年。對於這個利率，沒有辦法確定長期的期限結構。

另一個可能的選擇是存款類機構回購定盤利率。這是 CFETS 釋出的回購市場的新基準利率。顧名思義，這個利率是根據只有存款類機構的回購交易計算的。然而，在撰寫本文時，該利率的歷史資料仍然不足以支援任何結論性分析。我們留下這個新的利率用於未來的研究。

為了在數字上比較政府債券利率和 7D 回購利率，表 1 給出了平均貼現因子，假設相應的市場利率是無風險的。更準確地說，它報告了時間區間 \([t,t + \delta]\) 上的平均貼現因子，其中 \(t\) 是 2016 年 1 月 1 日至 2016 年 12 月 31 日的交易日。\(\delta\) 選擇為 1 年、3 年、5 年、7 年和 10 年。與政府債券利率相對應的貼現因子使用等式（3）以及 CCDC 公佈的利率曲線計算。7D 回購利率貼現因子是使用第 2.1 節中提到的自舉法計算的。

從表 1 可以看出，與政府債券利率相對應的貼現因子普遍大於 7D 回購利率，這與之前的分析一致。

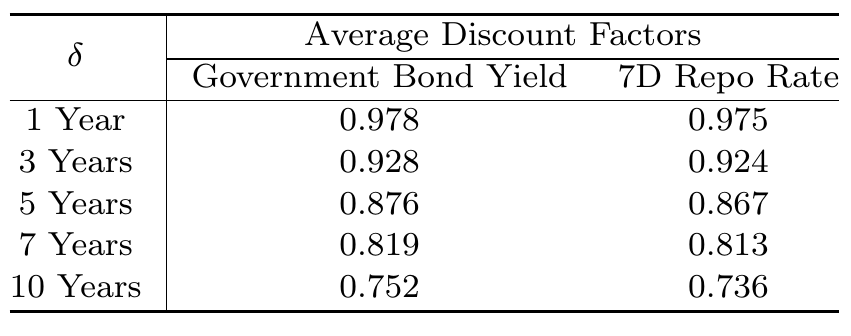
表 1，2016 年的平均貼現因子，分別對應中國政府債券利率和 7D 回購利率。

4. 數值測試

在中國市場，目前的市場慣例是使用單曲線估值等式（2）對 3M Shibor 互換定價。為了說明這種做法可能導致的估值偏差幅度，我們對 3M Shibor 利率互換合約進行估值。合約的選擇基於第 2.3 節中概述的標準，這使得雙曲線和單曲線貼現方法之間的估值差異顯著。

2013 年 12 月 26 日，CFETS 公佈的 5 年期 3M Shibor 互換利率為 5.6827%。該互換利率是根據主要市場參與者的報價計算得出的，並且很好地反映了當時的市場狀況。此後，中國市場的利率不斷下降。2016 年初，5 年期 3M Shibor 互換利率降至 3% 左右。

假設 2013 年 12 月 26 日簽署了一份名義價值為 100 萬元的 5 年期 3M Shibor 合同，互換率為 5.6827%。表 2 和圖 2 顯示了 2014 年至 2016 年的估值結果。合約分別使用當前的單曲線和雙曲線估值方法進行定價。在雙曲線貼現中，我們分別選擇 7D 回購利率和政府債券利率作為無風險利率。由於建議採用 7D 回購利率，因此將與該利率對應的結果作為基準。所有估值均來自固定利率接收方。

DV01 或一個基點的美元價值，是使用 7D 回購利率作為無風險利率的雙曲線貼現法獲得的。實際上，DV01 是通過將輸入的互換利率曲線⁹上下移動 x 個基點來計算的。我們分別用 \(V_{up}\) 和 \(V_{down}\) 表示估值結果

\[ DV01 = \frac{V_{up} - V_{down}}{2x}. \]

\(x\) 的選擇是經驗性的。CFETS 採用 \(x = 5\)（見 Lai [10]），而彭博採用 \(x = 10\)（見 Wu [11]）。我們遵循 CFETS 的選擇。

為了衡量估值差異的重要性，我們還報告了 DV01 的差異。該值的單位是基點。DV01 上 \(x\) 基點的差異解釋如下：如果通過 7D 回購利率貼現的估值是正確的，那麼使用相應方法導致的估值偏差相當於將輸入的 3M Shibor 互換利率曲線變動 \(x\) 基點。

關於估值結果有一些有趣的看點。首先，目前中國市場的做法是使用單曲線貼現法對 3M Shibor 互換定價。彭博和中國外匯交易中心的估值均接近表 2 的單曲線¹⁰欄中顯示的數字。與使用 7D 回購利率的雙曲線方法相比，目前的單曲線方法可能低估了 100 萬互換合約高達 1400 元人民幣。就 DV01 而言，差異達到 4.37 個基點，這意味著差異相當於將浮動利率曲線移動 4.37 個基點。在 2014 年至 2016 年的 749 個交易日內，平均估值差異和 DV01 差異分別為 701.47 元和 2.24 個基點。相比之下，從 2014 年到 2016 年，3M Shibor 的 5 年期互換利率每日絕對變化的中位數僅為 1.48 個基點。這些結果表明，在市場中使用當前的單曲線方法可能會嚴重低估固定利率接收方的互換合約，並給市場帶來很大的模型風險。

其次，如圖 2 所示，在採用 7D 回購利率的雙曲線法和單曲線法之間，估值差異先擴大，然後在合同簽訂一年半後達到最大值，然後下降。這種模式符合我們先前在第 2.3 節中的分析。在頭一年半的時間裡，市場利率不斷下降。因此，\((s^{fix}_{risky} - s_{risky}^{par})\) 擴大並主導了估值差異的變化。從 2015 年下半年開始，市場逐漸趨於穩定，\((s^{fix}_{risky} - s_{risky}^{par})\) 也是如此。在此期間，\((D_{rf} - D_{risky})\) 主導了這一變化。隨著互換合約的剩餘期限減少，\((D_{rf} - D_{risky})\) 變小，導致估值差異減少。

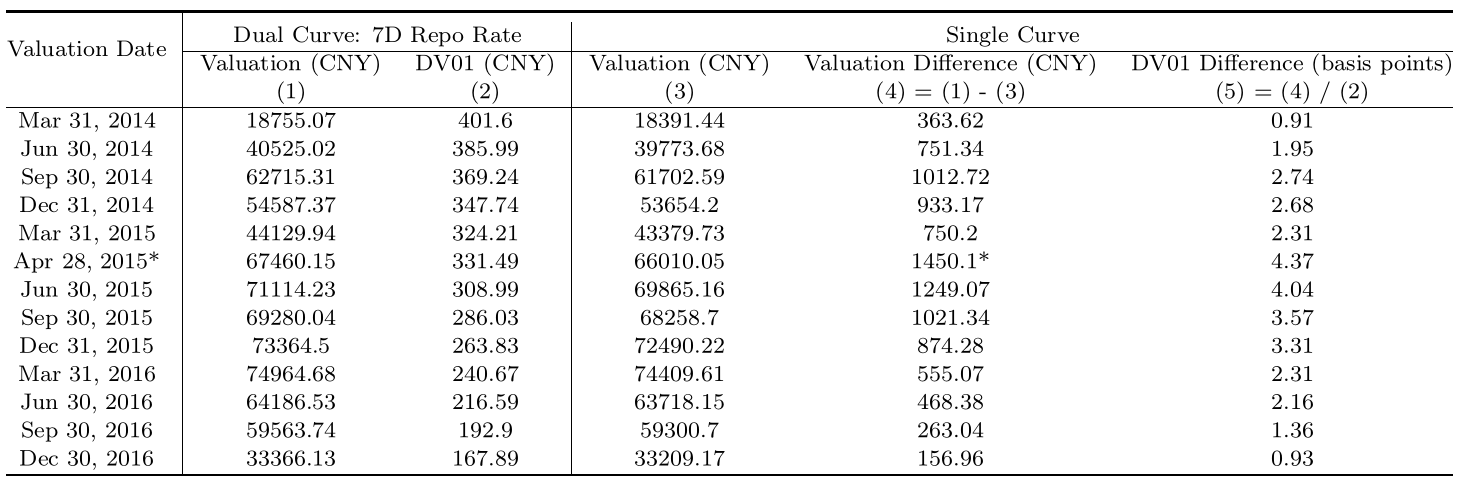
表 2，使用兩種方法估值 3M Shibor 互換合約，即單曲線貼現方法和使用 7D 回購利率的雙曲線貼現方法。該合約的價格於 2014 年至 2016 年每季度末定價。估值、DV01 和估值差異均以人民幣計價。為了衡量差異的重要性，估值差異也除以 DV01。

這兩種方法之間的估值差異在 2015 年 4 月 28 日達到最大值（標有\(*\)）。

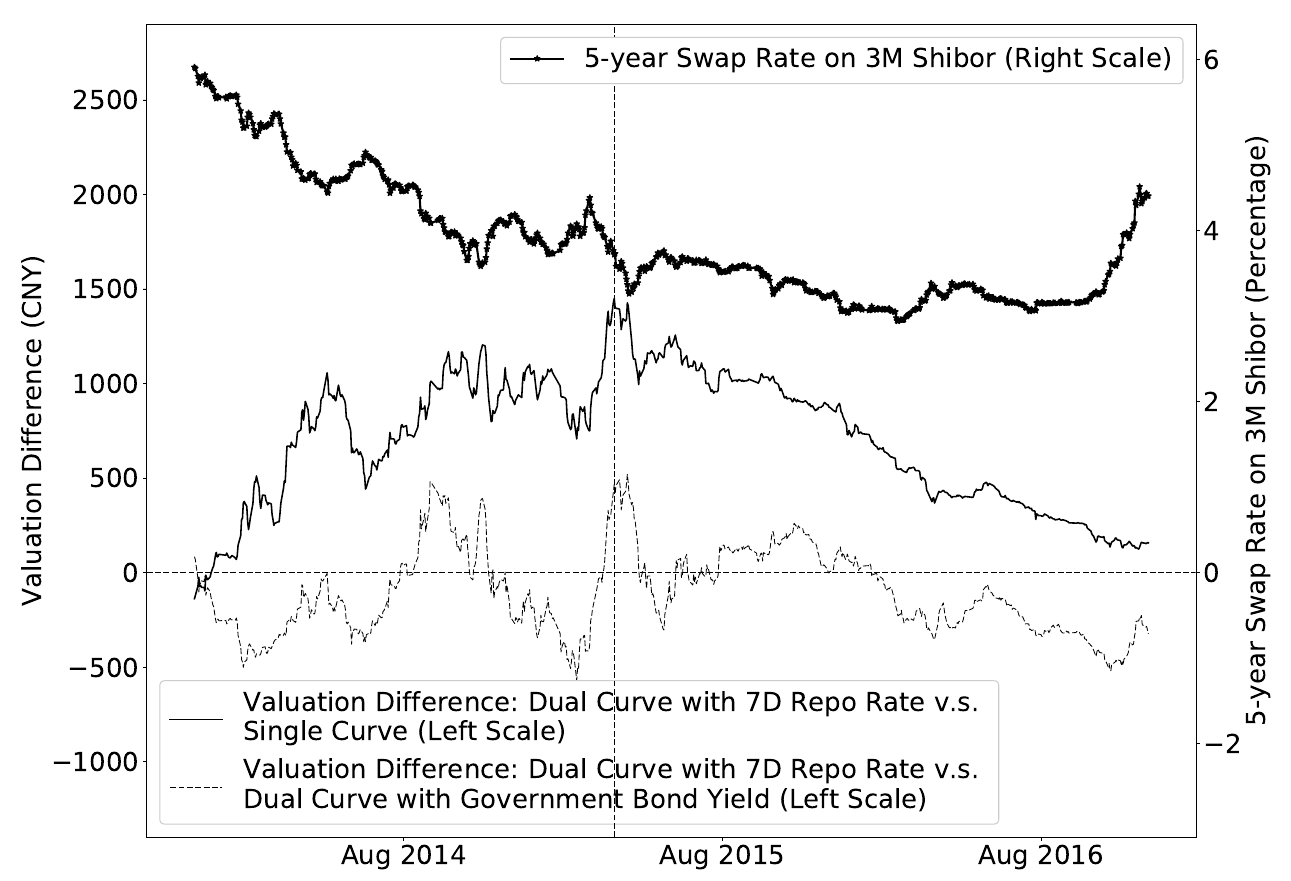
圖 2，左側比例：使用 7D 回購利率的雙曲線法與和單曲線法之間的估值差異，使用 7D 回購利率的雙曲線法與使用政府債券利率的雙曲線法之間的估值差異。右側比例：3M Shibor 互換的 5 年期互換利率。這些互換利率代表市場走勢。垂直線為 2015 年 4 月 28 日，使用 7D 回購利率的雙曲線法和單曲線法之間的估值差異達到最大值。

最後的觀察是，如圖 2 所示，在使用 7D 回購利率的雙曲線方法和使用政府債券利率的雙曲線方法之間，估值差異在大多數交易日是負的，這表明使用政府債券利率作為無風險利率會高估固定利率接收方的互換合約。這與表 1 中的結果一致，因為更高的貼現因子導致更高的估值結果。在 749 個交易日內，估值偏差幅度最大為 569.83 元人民幣，相當於 2.70 個基點的 DV01 差異。

5. 結論

在本文中，我們首先從理論上分析了單曲線貼現方法和雙曲線貼現方法的估值結果之間的差異。然後使用中國利率互換市場的資料驗證結論。我們已經證明，單曲線方法傾向於低估固定利率接收方的互換合約。對於仍然有很長存續期限的舊合約，且市場利率不斷下降的情況下偏差最為顯著。我們的數值測試表明，估值偏差的大小可能是中國互換市場中通常日間變動的 3 倍。本文的另一個重要討論是中國互換市場的無風險利率的選擇。在與中國政府債券利率和其他利率進行比較後，我們發現 7D 回購利率似乎是雙曲線貼現法最合適的選擇。我們希望這些結果能夠引起對中國市場利率互換估值問題的關注和洞察。

這項研究可以通過多種方式進行擴充套件。首先，為了選擇無風險利率，我們比較了市場中的三種不同利率。在這種比較中，我們意識到我們的支援論點是經驗性的。需要更系統的理由。其次，利率互換不是雙曲線框架中唯一需要估值的金融資產。此方法也適用於許多其他資產，例如貨幣互換（cross currency swap）和互換期權。看看估值方法的變化將如何影響這些資產在中國市場的估值將會很有趣。

參考文獻

1. P. Collin Dufresne and B. Solnik, On the term structure of default premia in the swap and libor markets, J. Financ. 56, 1095 (2001).
2. J. Hull and A. White, Libor vs. OIS: The derivatives discounting dilemma, Journal Of Investment Management 11, 14 (2012).
3. Z. Grbac and W. J. Runggaldier, Interest rate modeling: post-crisis challenges and approaches (Springer, 2015).
4. F. M. Ametrano and M. Bianchetti, Everything you always wanted to know about multiple interest rate curve bootstrapping but were afraid to ask (2013).
5. D. Filipovi and A. B. Trolle, The term structure of interbank risk, J. Financ. Econ. 109, 707 (2013).
6. M. Johannes and S. Sundaresan, The impact of collateralization on swap rates, J. Financ. 62, 383 (2007).
7. M. Henrard, Interest rate instruments and market conventions guide, OpenGamma Quantitative Research (2012).
8. D. Brigo and F. Mercurio, Interest rate models-theory and practice: with smile, inflation and credit (Springer Science & Business Media, 2007).
9. J. Hull, Options, futures and other derivatives, 3rd edn. (Pearson, 2015).
10. Y. Lai, Introduction to the interest rate swap intraday fixing curves, closing curves and valuation methodology, tech. rep., China Foreign Exchange Trading System (2012).
11. Z. Wu, DV01 Calculation Method, tech. rep., Bloomberg Professional (2011), Available at: subscription service.