機器學習篇三
目錄
十一、SVM
SVM,全稱是support vector machine,中文名叫支援向量機。SVM是一個面向資料的分類演算法,基本模型是在特徵空間中尋找間隔最大化的分離超平面的線性分類器。(間隔最大是它有別於感知機)
(1)當訓練樣本線性可分時,通過硬間隔最大化,學習一個線性分類器,即線性可分支援向量機;
(2)當訓練資料近似線性可分時,引入鬆弛變數,通過軟間隔最大化,學習一個線性分類器,即線性支援向量機;
(3)當訓練資料線性不可分時,通過使用核技巧及軟間隔最大化,學習非線性支援向量機。
1、SVM為什麼採用間隔最大化?
當訓練資料線性可分時,存在無窮多個分離超平面可以將兩類資料正確分開。感知機利用誤分類最小策略,求得分離超平面,不過此時的解有無窮多個。
線性可分支援向量機利用間隔最大化求得最優分離超平面,這時,解是唯一的
2、函式間隔和幾何間隔
函式間隔:
幾何間隔:
3、推導




4、KKT條件(凸優化問題)
1)對於無約束的優化問題,直接令梯度等於0求解。
2)對於含有等式約束的優化問題,拉格朗日乘子法,構造拉格朗日函式,令偏導為0求解。
3)對於含有不等式約束的優化問題,同樣構造拉格朗日函式,利用KKT條件求解。

5、SVM核函式的選擇
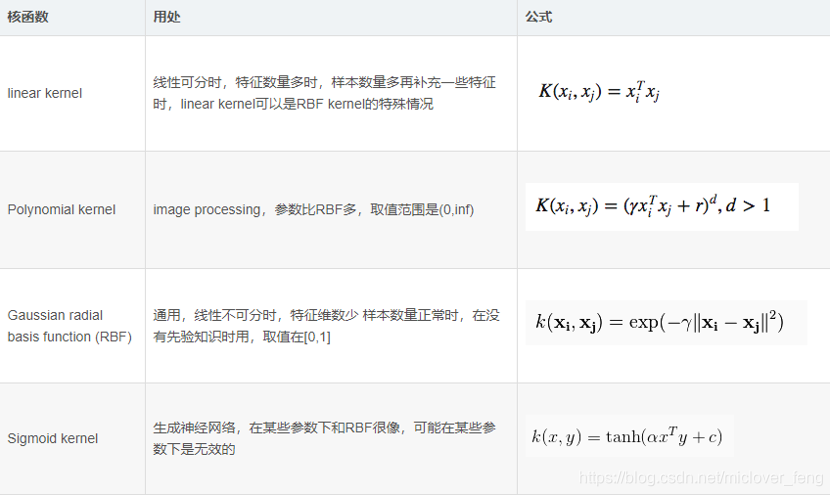
6、SVM演算法的主要優點和缺點:
優點:
1) 解決高維特徵的分類問題和迴歸問題很有效,在特徵維度大於樣本數時依然有很好的效果。
2) 僅僅使用一部分支援向量來做超平面的決策,無需依賴全部資料。
3) 有大量的核函式可以使用,從而可以很靈活的來解決各種非線性的分類迴歸問題。
4) 樣本量不是海量資料的時候,分類準確率高,泛化能力強。
缺點
1) 如果特徵維度遠遠大於樣本數,則SVM表現一般。
2) SVM在樣本量非常大,核函式對映維度非常高時,計算量過大,不太適合使用。
3)非線性問題的核函式的選擇沒有通用標準,難以選擇一個合適的核函式。
4)SVM對缺失資料敏感。
7、SVM為什麼會引入拉格朗日優化演算法?
更為高效的結局最優化問題
8、SVM投票機制
一對多法(one-versus-rest,簡稱OVR SVMs)
訓練時依次把某個類別的樣本歸為一類,其他剩餘的樣本歸為另一類,這樣k個類別的樣本就構造出了k個SVM。分類時將未知樣本分類為具有最大分類函式值的那類。
假如我有四類要劃分(也就是4個Label),他們是A、B、C、D。
於是我在抽取訓練集的時候,分別抽取
(1)A所對應的向量作為正集,B,C,D所對應的向量作為負集;
(2)B所對應的向量作為正集,A,C,D所對應的向量作為負集;
(3)C所對應的向量作為正集,A,B,D所對應的向量作為負集;
(4)D所對應的向量作為正集,A,B,C所對應的向量作為負集;
使用這四個訓練集分別進行訓練,然後的得到四個訓練結果檔案。
在測試的時候,把對應的測試向量分別利用這四個訓練結果檔案進行測試。
最後每個測試都有一個結果f1(x),f2(x),f3(x),f4(x)。
於是最終的結果便是這四個值中最大的一個作為分類結果。
評價:
這種方法有種缺陷,因為訓練集是1:M,這種情況下存在biased.因而不是很實用。可以在抽取資料集的時候,從完整的負集中再抽取三分之一作為訓練負集。
一對一法(one-versus-one,簡稱OVO SVMs或者pairwise)
其做法是在任意兩類樣本之間設計一個SVM,因此k個類別的樣本就需要設計k(k-1)/2個SVM。
當對一個未知樣本進行分類時,最後得票最多的類別即為該未知樣本的類別。
Libsvm中的多類分類就是根據這個方法實現的。
假設有四類A,B,C,D四類。在訓練的時候我選擇A,B; A,C; A,D; B,C; B,D;C,D所對應的向量作為訓練集,然後得到六個訓練結果,在測試的時候,把對應的向量分別對六個結果進行測試,然後採取投票形式,最後得到一組結果。
投票是這樣的:
A=B=C=D=0;
(A,B)-classifier 如果是A win,則A=A+1;otherwise,B=B+1;
(A,C)-classifier 如果是A win,則A=A+1;otherwise, C=C+1;
...
(C,D)-classifier 如果是A win,則C=C+1;otherwise,D=D+1;
The decision is the Max(A,B,C,D)
評價:這種方法雖然好,但是當類別很多的時候,model的個數是n*(n-1)/2,代價還是相當大的。
參考資料:
李航《統計學習方法》
http://www.cnblogs.com/jiangxinyang/p/9337094.html
https://blog.csdn.net/wjwfighting/article/details/82532847
https://www.cnblogs.com/pinard/category/894692.html
https://www.baidu.com/link?url=HfzWgzeRIWPH08txoXXCO7lJBotxDpxOfRDJE44TUY_-sKMQnXXrXZ7e3-Vs9BBsjKsd7ZXZ9v8_QjWj4fcIzNHVxZ8PnbhWOmUUvjeff0m&wd=&eqid=ffca968a000e7f22000000035bab7277
宣告:本人從網際網路蒐集了一些資料整理,由於查詢資料太多,好多內容出處不能記得,如有侵權內容,請各位博主及時聯絡我,我將盡快修改,並註明出處,再次感謝各位廣大博主的資料。
