Perception感知器（用於線性二分類）

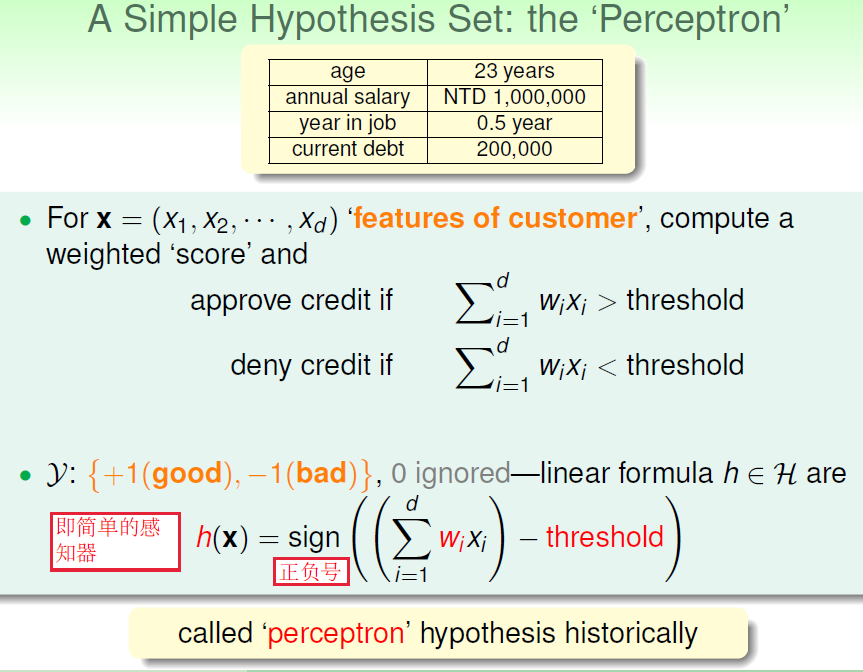
PLA演算法：怎樣從假設空間中找到g$H$$g$

1.目標：克約等於女，最好的結果，但是˚F未知此方法不行

2.目標：使得在給定資料上兩者預測結果接近

3.感知器優化演算法（PLA）

上述公式的理解：
（1）y是正的，出來結果w是負的

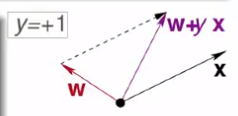
通過w + x，講w拉回來一點（作為新的分介面法向量，​​此圖中黑色x為原分介面法向量）

（ 2）Y是負的，出來結果瓦特正的英文的

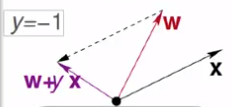
通過W + X，講瓦特拉過去一點

舉例：

（1）最開始沒有線


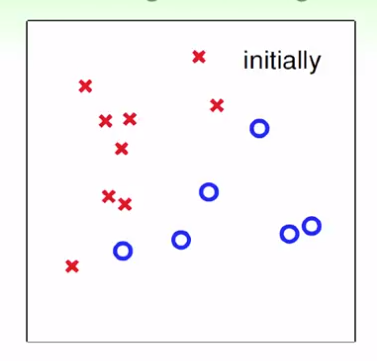
（2）預設每個點都是錯的，找到任意一點與原點連線（原點在圖中間），而這個點剛好為正（圈為正，叉為負），即為分介面的法向量



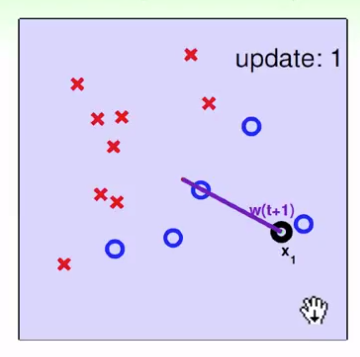
（3）
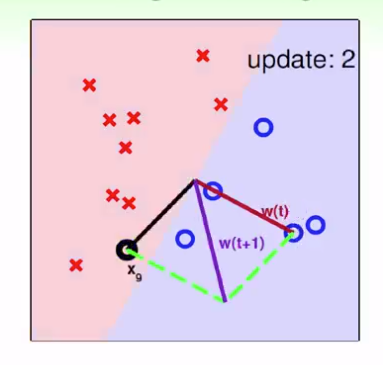
黑點為分類錯誤的點，與原法向量相加，產生紫色線，即可以調整分介面，紫色作為新的法向量，如此持續，沒有直到分類照片錯誤


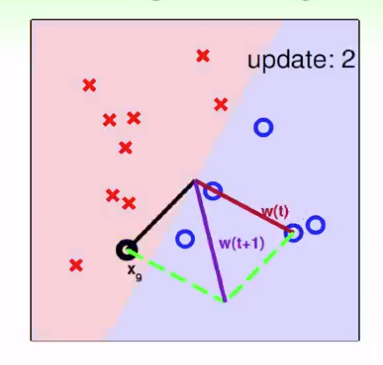
思考：

解放軍終止條件

1.PLA保證：資料必須線性可分


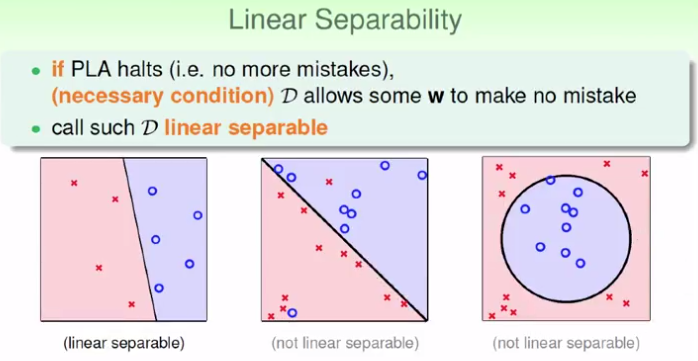
2.PLA條件1：線性可分


3.PLA條件2：有錯才更新


結合條件1和2的結論：令

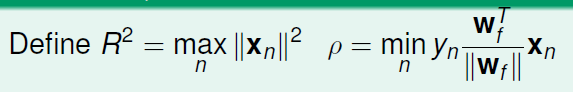
則由（1）得：
對於第T次更新，

（因為）：$w_0=0$

由（2）得

對於第Ť次更新，

$||w_T||^2 > ||w_0||^2+T*R^2=T*R^2$

從而（1）結果除以（2）：
$\frac{w_f^T*w_T}{||w_T||})> \frac{T*\rho*||w_f||}{\sqrt{T}*R}$

$\frac{w_f^T*w_T}{||w_T||*||w_f||}> \sqrt{T}\frac{\rho}{R}$

而$\frac{w_f^T*w_T}{||w_T||*||w_f||}$ 即兩個向量的相似度，最大不超過1，故

$1 > \sqrt{T}\frac{\rho}{R}$，最大更新次數 T 不超過 $\frac{R^2} {\rho^2}$

PLA優缺點分析

（1）優點：比較容易去實現
（2）缺點：
1.假定資料線性可分，但事實上我們不知道資料的分佈
2.不確定多久才會終止，因為上述條件中的 $\rho$ 與 $w_f$ 有關，但 $w_f$ 未知

解決上述缺點

即使資料線性可分，當資料有噪聲時PLA應該如何停止？

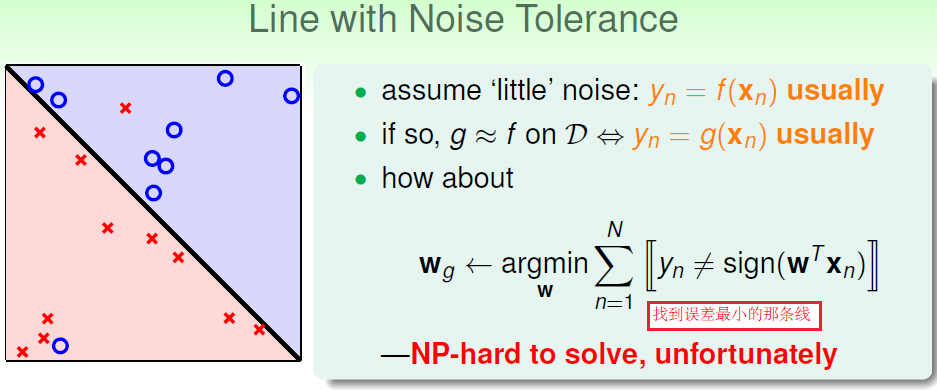
解決方法：
1.口袋演算法（貪心演算法，PLA的一個變形）

兩者比較：

當線性可分時，口袋演算法對於每條線，需要找出所有錯誤分類的點，而PLA只需要找到一個即可