ACM-ICPC 2018 world final A題 Catch the Plane
題目連線:https://icpc.kattis.com/problems/catch
Catch the Plane
Your plane to the ICPC Finals departs in a short time, and the only way to get to the airport is by bus. Unfortunately, some of the bus drivers are considering going on strike, so you do not know whether you can get to the airport on time. Your goal is to plan your journey in such a way as to maximize the probability of catching your plane.
You have a detailed map of the city, which includes all the bus stations. You are at station 00 and the airport is at station 11. You also have a complete schedule of when each bus leaves its start station and arrives at its destination station. Additionally, for each bus you know the probability that it is actually going to run as scheduled, as opposed to its driver going on strike and taking the bus out of service. Assume all these events are independent. That is, the probability of a given bus running as planned does not change if you know whether any of the other buses run as planned.
If you arrive before the departure time of a bus, you can transfer to that bus. But if you arrive exactly at the departure time, you will not have enough time to get on the bus. You cannot verify ahead of time whether a given bus will run as planned – you will find out only when you try to get on the bus. So if two or more buses leave a station at the same time, you can try to get on only one of them.
![\includegraphics[width=0.5\textwidth ]{catch2}](https://icpc.kattis.com/problems/catch/file/statement/en/img-0001.png)
Consider the bus schedule shown in Figure 1. It lists the start and destination stations of several bus routes along with the departure and arrival times. You have written next to some of these the probability that that route will run. Bus routes with no probability written next to them have a 100%100% chance of running. You can try catching the first listed bus. If it runs, it will take you straight to the airport, and you can stop worrying. If it does not, things get more tricky. You could get on the second listed bus to station 22. It is certain to leave, but you would be too late to catch the third listed bus which otherwise would have delivered you to the airport on time. The fourth listed bus – which you can catch – has only a 0.10.1 probability of actually running. That is a bad bet, so it is better to stay at station 00 and wait for the fifth listed bus. If you catch it, you can try to get onto the sixth listed bus to the airport; if that does not run, you still have the chance of returning to station 0 and catching the last listed bus straight to the airport.
Input
The first line of input contains two integers mm (1≤m≤1061≤m≤106) and nn (2≤n≤1062≤n≤106), denoting the number of buses and the number of stations in the city. The next line contains one integer kk (1≤k≤10181≤k≤1018), denoting the time by which you must arrive at the airport.
Each of the next mm lines describes one bus. Each line contains integers aa and bb (0≤a,b<n0≤a,b<n, a≠ba≠b), denoting the start and destination stations for the bus. Next are integers ss and tt (0≤s<t≤k0≤s<t≤k), giving the departure time from station aa and the arrival time at station bb. The last value on the line is pp (0≤p≤10≤p≤1, with at most 1010 digits after the decimal point), which denotes the probability that the bus will run as planned.
Output
Display the probability that you will catch your plane, assuming you follow an optimal course of action. Your answer must be correct to within an absolute error of 10−610−6.
| Sample Input 1 | Sample Output 1 |
|---|---|
8 4 1000 0 1 0 900 0.2 0 2 100 500 1.0 2 1 500 700 1.0 2 1 501 701 0.1 0 3 200 400 0.5 3 1 500 800 0.1 3 0 550 650 0.9 0 1 700 900 0.1 |
0.3124 |
| Sample Input 2 | Sample Output 2 |
|---|---|
4 2 2 0 1 0 1 0.5 0 1 0 1 0.5 0 1 1 2 0.4 0 1 1 2 0.2 |
0.7 |
Icpc2018 題目A:趕飛機
你乘坐的去ICPC總決賽的飛機很快就要起飛了,前往機場的唯一方式是乘坐公交車。 不幸的是,一些公交車司機正在考慮罷工,所以你不知道能否按時到達機場。你的目標是規劃路線使趕上飛機的可能性最大化。
你有一份標有所有公交車站的這座城市的詳細地圖。你在0站,機場在1站。你也有一份完整的每輛公交車出發時間和到達時間的計劃表。除此之外,知道每輛公交車實際按照計劃表執行的可能性,而不是司機罷工的可能性。假設所有事件相互獨立,也就是說,如果知道任何其他公交車是否按計劃執行,則給定公交車按計劃執行的概率不會改變。
如果你能在公交車離開之前到達,就能換乘該公交車。但是如果你正好的公交車離開的時間到達則沒有足夠的時間上車。你無法提前驗證給定的公交車是否按計劃執行—只有當嘗試上車時才會發現。所以當有兩輛或更多公交車同時離開公交站,你只能嘗試上其中一輛車。
| 公交車時間表 |
|||
| 起始站 |
目的站 |
離開時間 |
到達時間 |
| 0 |
1 |
0(20%) |
900 |
| 0 |
2 |
100 |
500 |
| 2 |
1 |
500 |
700 |
| 2 |
1 |
501(10%) |
701 |
| 0 |
3 |
200(50%) |
400 |
| 3 |
1 |
500(10%) |
800 |
| 3 |
0 |
550(90%) |
650 |
| 0 |
1 |
700(10%) |
900 |
表 A.1:對應樣例輸入1的公交時間表
考慮圖A.1中所示的公交時刻表。它列出了幾條公交線路的起點和終點站以及出發和到達時間。你已經在其中一些中寫下了該路線執行的概率。沒有寫在他們旁邊的概率的公交車路線有100%的執行機會。你可以嘗試追上第一個列出的公共汽車。如果它執行,它會帶你直接去機場,你可以不用擔心。如果沒有,事情變得更加棘手。你可以乘坐第二輛列車前往2號站。它肯定會離開,但是你趕不上第三輛列出的公共汽車,否則它會按時送你到機場。第四個列出的公共汽車可以追上但只有0.1的實際執行概率。這是一個糟糕的賭注,所以最好留在0號站並等待第五輛列出的公交車。如果你趕上它,你可以嘗試乘坐第六輛到達機場的列車;如果沒有執行,你仍然有機會返回0號站並將最後一輛列出的公共汽車直接送往機場。
輸入:
第一行輸入兩個整數m,n(1=<m<=10^6,2=<n<=10^6), 表示公共汽車的數量和城市的車站數量.接下來的一行一個整數k(1=<k<=10^18),表示你必須達到機場的時間。
接下來的m行中的每一行都描述一輛公交車。每行包括整數a和b(0=<a,b<n,a!=b),表示該公交的起始站和終點站。接下來是整數s和t(0=<s<t<k),給定從站點a的離開時間和到達站點b的時間。最後一行是p(0=<p<=1,最多精確到小數點後10位),表示公交車按計劃執行的概率。
輸出:
假設你遵循最佳行動方案,表示你將趕上你的飛機的概率。你的答案必須正確,絕對誤差為10^-6。
理解題意
給定一系列的公交車,在本報告中對其編號(從1到M),可以乘坐任何公交前往飛機場,但其中有如下限制與難點:
- 公交車出發的是有概率的,記為P。有P的可能性開車,有(1-P)的可能性不開車。
- 若要換乘公交車,上一輛的到達時間一定要早於下一輛的出發時間。
- 求出到達飛機場的最大概率。也就是說,在有多種選擇的情況下,要選取概率最高的路線。在該路線概率最大的情況下,其子路線肯定也是概率最大的,這就引出了動態規劃演算法。
- 題目資料量很大,k的範圍是[1,10^18],所以C++需要用long long。
- 給出的公交車很多,甚至有時間超過k的,相同站點和時間的,要想百分百AC,這些細節需要把握。
現在開始分析樣例,見下面的手繪圖,其中左圖的①②③……為輸入樣例中的公交車標號;後面的五個數字為該車的資訊(出發站,目的站,出發時間,到達時間,開車概率)。右邊的樹狀圖為分析圖,①②③……表示使用該公交車;左右孩子中的左分支表示開車(並帶有開車的概率),右分支表示不開車(並帶有不開車的概率);☆為到達終點(並帶有該路線下的總概率);在有多種選擇的情況下,要選取概率最高的路線作為子路線。
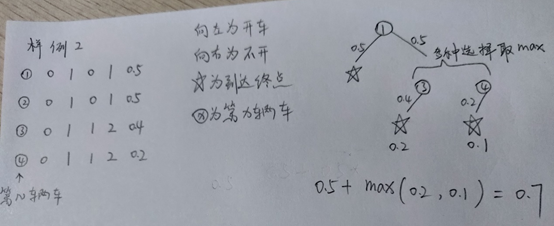
樣例2的圖解:選擇公交車①,開車概率為0.5,可直接到達飛機場,總概率0.5。公交車①不開車的概率為0.5,此情況下,可以選擇兩種路線,選擇公交車③,有0.4的概率開車併到達飛機場,該路線的總概率為0.5*0.4=0.2;選擇公交車④,有0.2的概率開車併到達飛機場,該路線的總概率為0.5*0.2=0.1;選擇最優子結果,即概率為0.2的線路。最終總概率為0.5+0.2=0.7。
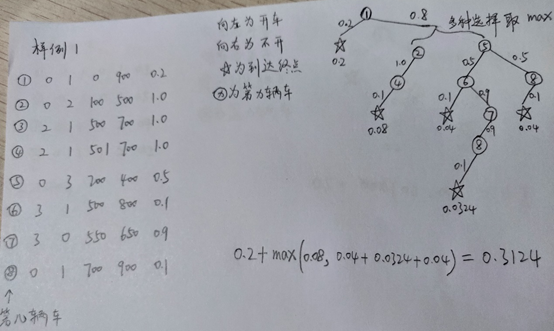
樣例1的圖解:選擇公交車①,開車概率為0.2,可直接到達飛機場,總概率為0.2。公交車①不開車的概率為0.8,存在兩種路線,兩種路線按照上面一樣的分析方法,左孩子的路線概率為0.8*1.0*0.1=0.08;右孩子的路線概率為0.5*0.1+0.5*0.9*0.9*0.1+0.5*0.1=0.1124;選擇概率大的路線,即0.1124。最終總概率為0.2+0.1124=0.3124。
設計演算法
既然分析出了需要動態規劃,就需要設計狀態轉移方程。要計算從車站0到飛機場的概率,那麼對應上圖(第三節的兩張手繪圖)的樹該如何構造和求解呢?
- 首先就要掃描所有可能的公交車。因為要構造的是樹,只有已知整條路徑的概率才能得到總概率,所以需要從下到上構造樹。為了能從下到上構造,那麼就需要從飛機場開始往回倒推DP,做法是:按照開車時間逆序來掃描所有的公交車,這樣就能正確地更新父節點的概率值。
- 計算概率值。已知公交車的掃描順序,那麼就需要計算對應節點的概率值。每個公交車都有開車和不開車兩種情況,所以分兩種情況累加概率值。由於車況複雜,每種情況可能都有各自的子結構,為了最大化概率,選擇最優子結構,以此完成DP的概率計算。
經過以上分析,DP狀態轉移方程如下:
dp[node]=P*dp[destination]+(1-P)*dp[start]
dp[node]=max(dp[node], dp[child1], dp[child2], dp[child3], …)
資料結構的設計與解釋:Bus結構體對應了樹的節點如下,包括起始站、終點站、開車時間、到達時間、開車概率、路線總概率。其中的運算子過載保證了sort()函式排序的有效性。自寫的cmp函式保證了公交車的掃描順序為開車時間的逆序。
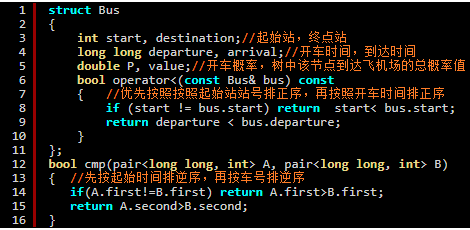
資料結構建好之後,為了優化空間,不直接建立樹結構,而是按照時間從後往前更新,保證樹結構的正確性即可。需要更新的值就是結構體中的value,虛擬碼如下所示:
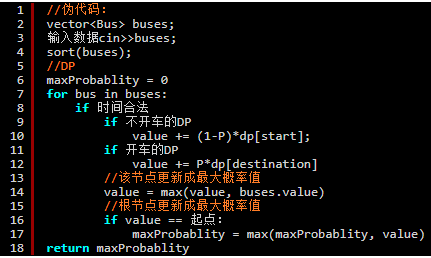
//虛擬碼:
vector<Bus> buses;
輸入資料cin>>buses;
sort(buses);
//DP
maxProbablity = 0
for bus in buses://時間逆序掃描
if 時間合法
if 不開車的DP
value += (1-P)*dp[start];
if 開車的DP
value += P*dp[destination]
//該節點更新成最大概率值
value = max(value, buses.value)
//根節點更新成最大概率值
if value == 起點:
maxProbablity = max(maxProbablity, value)
return maxProbablity
/* 提交連結:https://icpc.kattis.com/problems/catch 執行時間:2.35 佔用記憶體:3158bytes */ #include <algorithm> #include <cstdio> #include <iostream> #include <vector> using namespace std; struct Bus { int start, destination;//起始站,終點站 long long departure, arrival;//開車時間,到達時間 double P, value;//開車概率,樹中該節點到達飛機場的總概率值 bool operator<(const Bus& bus) const { //優先按照按照起始站站號排正序,再按照開車時間排正序 if (start != bus.start) return start< bus.start; return departure < bus.departure; } }; bool cmp(pair<long long, int> A, pair<long long, int> B) { //先按起始時間排逆序,再按車號排逆序 if(A.first!=B.first) return A.first>B.first; return A.second>B.second; } int main() { int M, N; long long K; while (cin >> M >> N >> K) { //公交車結構體陣列 vector<Bus> buses(M+1); for (int i = 0; i < M; i++) { cin >> buses[i].start >> buses[i].destination >> buses[i].departure >> buses[i].arrival >> buses[i].P; buses[i].value = 0.0; } //將飛機場資訊加入公交車陣列 buses[M].start = 1; buses[M].departure = K+1; buses[M].value = 1.0; sort(buses.begin(), buses.end()); //車號陣列,方便找到車號。 vector<pair<long long, int> > orders(M+1); //開車時間,車號 for (int i = 0; i <= M; i++) orders[i] = make_pair(buses[i].departure, i); sort(orders.begin(), orders.end(), cmp); //符號為了排序方便。假設沒有符號。先按起始時間排逆序,再按車號排逆序 //開始DP求概率 double maxProbablity = 0.0; for (int i = 0; i <= M; i++) if (orders[i].first <= K) //出發時間在限制之內 { int number = orders[i].second; //車號 Bus& r = buses[number]; r.value = 0.0; //不開車 Bus r2; r2.start = r.start; r2.departure = r.departure; vector<Bus>::iterator it = upper_bound(buses.begin(), buses.end(), r2); if (it != buses.end() && it->start == r.start) //可以選擇這個車 r.value += (1.0-r.P) * it->value; // 錯過這班車 //開車 r2.start = r.destination; r2.departure = r.arrival; it = upper_bound(buses.begin(), buses.end(), r2); if (it != buses.end() && it->start == r.destination) //可以選擇這個車 r.value += r.P * it->value; // 趕上了這班車 //在所有子結構中,更新出最大概率 if (number < M && buses[number+1].start == buses[number].start) r.value = max(r.value, buses[number+1].value); //該站是0,更新結果 if (r.start == 0) maxProbablity = max(maxProbablity, r.value); } printf("%0.10lf\n", maxProbablity); } }
