DirectX11--HLSL中矩陣的記憶體佈局和mul函式探討
前言
說實話,我感覺這是一個大坑,不知道為什麼要設計成這樣混亂的形式。
在我用的時候,以row_major矩陣,並且mul函式以向量左乘矩陣的形式來繪製時的確能夠正常顯示,並不會有什麼感覺。但是也有人會遇到明明傳的矩陣沒有問題,卻怎麼樣都繪製不出的情況;或者使用列矩陣,在mul函式用向量左乘的形式卻又可以繪製出來的疑問。因此本文目的就是要掃清這些障礙。
ps. 本問題由淡一抹夕霞提供。
DirectX11 With Windows SDK完整目錄
歡迎加入QQ群: 727623616 可以一起探討DX11,以及有什麼問題也可以在這裡彙報。
一些線性代數基礎
行主矩陣與列主矩陣
首先要了解的是,行主矩陣是這樣的:
\[ \mathbf{M}=\begin{bmatrix} m_{11} & m_{12} & m_{13} & m_{14} \\ m_{21} & m_{22} & m_{23} & m_{24} \\ m_{31} & m_{32} & m_{33} & m_{34}\\ m_{41} & m_{42} & m_{43} & m_{44} \end{bmatrix}\]
而列主矩陣是這樣的:
\[ \mathbf{M}=\begin{bmatrix} m_{11} & m_{21} & m_{31} & m_{41} \\ m_{12} & m_{22} & m_{32} & m_{42} \\ m_{13} & m_{23} & m_{33} & m_{43}\\ m_{14} & m_{24} & m_{34} & m_{44} \end{bmatrix}\]
行主矩陣經過一次轉置後就會變成列主矩陣
矩陣左乘與右乘
由於矩陣乘法不滿足交換律,則需要區分當前矩陣位於乘號的左邊還是右邊。有時候經常都會聽到左乘和右乘這兩個概念,下面是有關它們的含義:
左乘指的是該矩陣位於乘號的左邊,例如:行向量 左乘 矩陣,即行向量在乘號的左邊
右乘指的是該矩陣位於乘號的右邊,例如:列向量 右乘 矩陣,即列向量在乘號的右邊
ps. 向量也是矩陣
行向量v和矩陣M滿足下面的關係:
\[ \mathbf{(vM)}^{T} = \mathbf{M}^{T} \mathbf{v}^{T} \]
C++和HLSL中矩陣的記憶體佈局
在C++的DirectXMath中,無論是XMFLOAT4X4
XMMATRIX,都是採用行主矩陣的儲存方式。在連續記憶體中的佈局是這樣的:\[ m_{11} \; m_{12} \; m_{13} \; m_{14} \; m_{21} \; m_{22} \; m_{23} \; m_{24} \; m_{31} \; m_{32} \; m_{33} \; m_{34} \; m_{41} \; m_{42} \; m_{43} \; m_{44}\]
在C++傳遞給HLSL的位元組流資料是不會發生變化的,這一點可以通過VS自帶的圖形偵錯程式可以察看。
但是資料傳遞給HLSL後,matrix(float4x4)的屬性決定如何去接受這些資料。
預設情況下,matrix(float4x4)是列矩陣,這意味著它會按列主矩陣的形式進行選取,相當於進行了一次轉置。
如果想讓它按行主矩陣的形式進行選取,則應當在前面加上row_major修飾符以避免"轉置"。
HLSL中的mul函式
微軟的官方文件是這麼描述mul函式的(微軟官方文件連結),這裡進行個人翻譯:
使用矩陣數學來進行矩陣x左乘矩陣y的運算,要求矩陣x的列數與矩陣y的行數相等。
如果x是一個向量,那麼它將被解釋為行向量。
如果y是一個向量,那麼它將被解釋為列向量。
表面上看起來很美滿,很智慧,但稍有不慎就要在這裡踩大坑了。
dp4指令
dp4是一個彙編指令(微軟官方文件連結),使用方法如下:
dp4 dst, src0, src1
其中 src0和src1是一個向量,計算它們的點乘並將結果傳給dst。
當然這裡並不是要教大家怎麼寫彙編,而是怎麼看。
為了瞭解mul函式是如何進行向量與矩陣的乘法運算,我們需要探討一下它的彙編實現。這裡我所使用的是row_major矩陣。首先是向量作為第一個引數的情況:
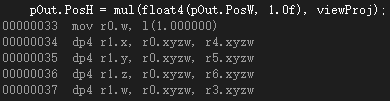
可以看到這種運算方式實際上卻是按照向量右乘矩陣的形式進行的運算。
然後是將向量作為第二個引數的情況(僅單純的引數交換):
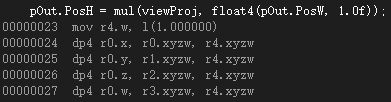
無論是行向量左乘矩陣,還是列向量右乘矩陣,在彙編層面上都是用dp4的形式進行計算,這是因為對矩陣來說在記憶體上是以4個行向量的形式儲存的,傳遞一行比傳遞一列更簡單,適合進行與列向量的運算,並且效率會更高。
但是交換兩個引數卻會導致運算結果/顯示結果的不同,這時候就要看看矩陣所存的值了。
先看一段HLSL程式碼:
struct VertexPosNormalTex
{
float3 PosL : POSITION;
float3 NormalL : NORMAL;
float2 Tex : TEXCOORD;
};
struct VertexPosHWNormalTex
{
float4 PosH : SV_POSITION;
float3 PosW : POSITION; // 在世界中的位置
float3 NormalW : NORMAL; // 法向量在世界中的方向
float2 Tex : TEXCOORD;
};
// 頂點著色器
VertexPosHWNormalTex VS(VertexPosNormalTex pIn)
{
VertexPosHWNormalTex pOut;
row_major matrix viewProj = mul(gView, gProj);
pOut.PosW = mul(float4(pIn.PosL, 1.0f), gWorld).xyz;
pOut.PosH = mul(float4(pOut.PosW, 1.0f), viewProj);
pOut.NormalW = mul(pIn.NormalL, (float3x3) gWorldInvTranspose);
pOut.Tex = pIn.Tex;
return pOut;
}我們只考慮viewProj的初始化和pOut.PosH的賦值操作。
首先是viewProj原本的值:

這是向量左乘矩陣時四個向量暫存器的值(預設HLSL):

這是向量右乘矩陣時四個向量暫存器的值(將float4(pOut.PosW, 1.0f)和viewProj交換):
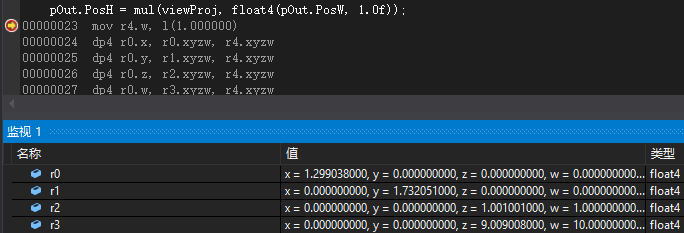
可以發現這裡面隱含了一次轉置操作。這裡的轉置不是空穴來風,而是源自於這句話前面的程式碼(預設HLSL):

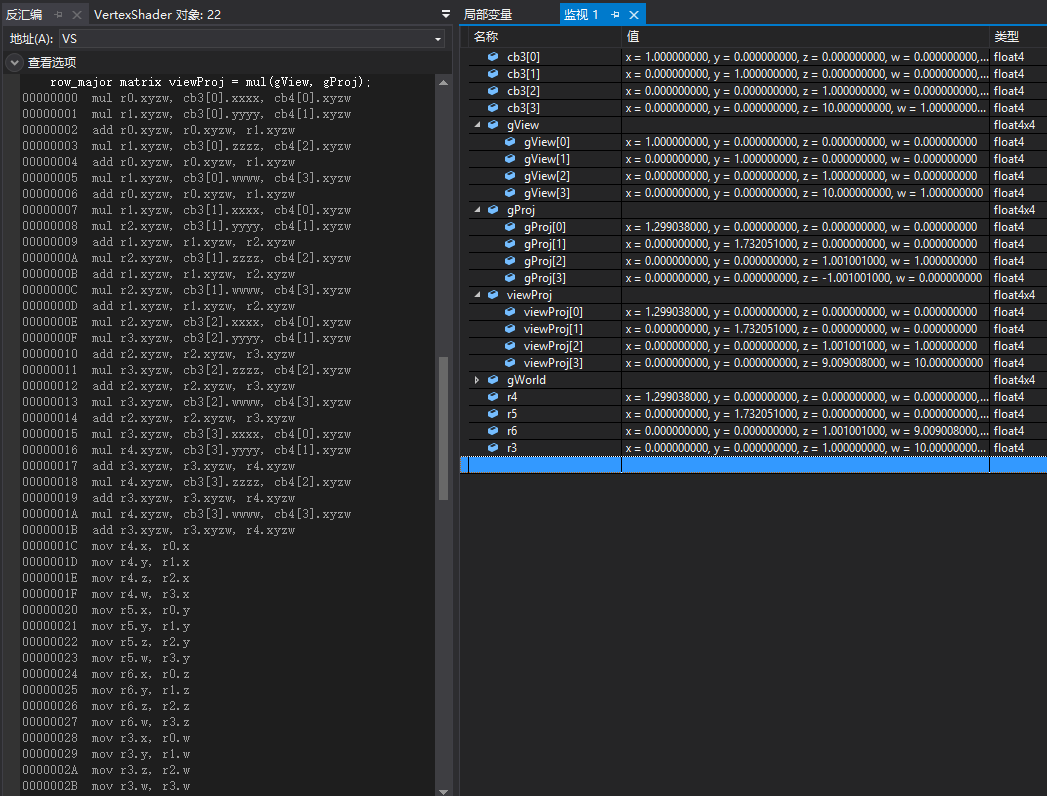
而將float4(pOut.PosW, 1.0f)和viewProj交換後,則彙編程式碼沒有了轉置操作:

因此,我們可以知道一個行向量左乘行主矩陣時,為了滿足mul函式使用dp4指令優化運算,很可能會預先對原來的矩陣進行轉置。其中r4 r5 r6 r3為viewProj轉置後的矩陣,即將會左乘向量float4(pOut.PosW, 1.0f)
總結
綜上所述,有三處地方可能會發生轉置:
- C++程式碼端的轉置
- HLSL中matrix(float4x4)是列主矩陣時會發生轉置
- mul乘法內部是以列向量右乘矩陣的形式實現的,對於行向量左乘矩陣的情況會發生轉置
經過組合,就一共有四種能夠正常繪製的情況:
- C++程式碼端不進行轉置,HLSL中使用
row_major matrix,mul函式使用行向量左乘矩陣。這種方法易於理解,但是在HLSL中很可能會產生用於轉置矩陣的大量指令,效能上略有損失。 - C++程式碼端進行轉置,HLSL中使用
matrix,mul函式使用行向量左乘矩陣。這是官方例程所使用的方式,可以避免HLSL的轉置,但是在理解上可能會有所困惑,容易陷入為什麼不是使用列向量右乘矩陣的迷思中。後續我會將教程的專案也使用這種方式,但是為了在使用上能表現得更像是向量(矩陣)左乘矩陣的形式,在C++端矩陣仍然按行主矩陣傳入,但通過一些手段在內部隱藏轉置操作,然後在HLSL端也統一用向量(矩陣)左乘矩陣的思想來編寫著色器程式碼。 - C++程式碼端不進行轉置,HLSL中使用
matrix,mul函式使用列向量右乘矩陣。這種方法的確可行,效率上和2等同,就是HLSL那邊的矩陣乘法都要反過來寫,對於適應了左乘寫法的人來說不建議使用這種方式。 - C++程式碼端進行轉置,HLSL中使用
row_major matrix,mul函式使用列向量右乘矩陣。就算這種方法也可以繪製出來,但還是很讓人難受,比第2點還難受。
也就是說,以組合1為基準,任意改變其中兩個狀態(即轉置兩次)都不會影響最終結果。
DirectX11 With Windows SDK完整目錄
歡迎加入QQ群: 727623616 可以一起探討DX11,以及有什麼問題也可以在這裡彙報。
