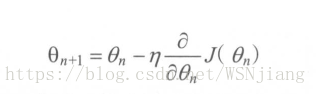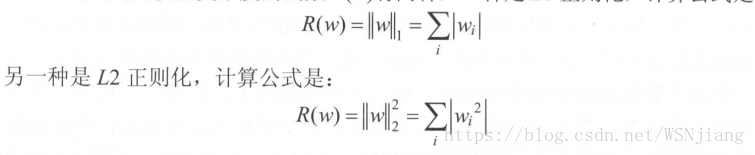Tensorflow學習筆記(3)
深層神經網路,目前TensorFlow提供了7種不同的非線性啟用函式, tf.nn.relu 、tf.sigrnoid和tf.tanh是其中比較常用的幾個。當然,TensorFlow 也支援使用自己定義的啟用函式 。簡單eg:異或運算(同為0,異為1)
通過神經網路解決多分類問題最常用的方法是設定n個輸出節點,其中n為類別的個數。對於每一個樣例,神經網路可以得到的一個n維陣列作為輸出結果.陣列中的每一個維度(也就是每一個輸出節點)對應一個類別。
Softmax迴歸本身可以作為一個學習演算法來優化分類結果,但在TensorFlow中,softmax迴歸的引數被去掉了,它只是一層額外的處理層,將神經網路的輸出變成一個概率分佈。
在實現交叉熵的程式碼中直接將兩個矩陣通過“*”操作相乘。這個操作不是矩陣乘法,而是元素之間直接相乘。矩陣乘法需要使用tf.matmul函式來完成。
因為交叉熵一般會與softmax迴歸一起使用,所以TensorFlow對這兩個功能進行了統一封裝,並提供了tf.nn.softmax_cross_entropy_with_logits()函式。在只有一個正確答案的分類問題中,TensorFlow提供了tf.nn.sparse_softmax_cross_entropy_with_logits函式來進一步加速計算過程。
迴歸問題解決的是對具體數值的預測。比如房價預測、銷量預測等都是迴歸問題。這些問題需要預測的不是一個事先定義好的類別,而是一個任意實數。解決迴歸問題的神經網路一隻有一個輸出節點,這個節點的輸出值就是預測值。對於迴歸問題,最常用的損失函式是均方誤差(MSE,mean squared error)。
函式為:tf.reduce_mean(tf.square(y_y_))
引數的梯度可以通過求偏導的方式計算,對於引數 θ ,其梯度為主J(θ)。有了θ梯度,還需要定義一個學習率(learning rate)來定義每次引數更新的幅度。從直觀上理解,可以認為學習率定義的就是每次引數移動的幅度。引數更新公式為:
學習率的設定:通過指數衰減的學習率既可以讓模型在訓練的前期快速接近較優解,又可以保證模型在訓練後期不會有太大的波動,從而更加接近區域性最優。
tf.train.exponential_ decay函式實現了指數衰減學習率。通過這個函式,可以先使用較大的學習率來快速得到一個比較優的解,然後隨著迭代的繼續逐步減小學習率,使得模型在訓練後期更加穩定。exponential_decay函式會指數級地減小學習率,
正則化的思想就是在損失函式中加入刻畫模型複雜程度的指標。假設用於刻畫模型在訓練資料上表現的損失函式為j(θ)的,那麼在優化時不是直接優化j(θ)的,而是優化J(θ)+λR(w)。其中R(w)刻畫的是模型的複雜程度,而λ表示模型複雜損失在總損失中的比例。注意這裡θ表示的是一個神經網路中所有的引數,它包括邊上的權重w和偏置項b。一般來說模型複雜度只由權重w決定。常用的刻畫模型複雜度的函式 R(w)有兩種,公式為:
tensorflow函式為:tf.contrib.layers.l1_regularizer(lamba)(w)和tf.contrib.layers.l2_regularizer(lamba)(w)。tensorflow 通過集合在計算圖上儲存張量,通過呼叫計算圖來提取正則化所需要的W。