【題目大意】在某塊平面土地上有N個點，你可以選擇其中的任意四個點，將這片土地圍起來，當然，你希望這四個點圍成的多邊形面積最大。

【資料範圍】4≤n≤2000, |x|,|y|<=100000

【思路】毫無疑問，這四個點肯定在凸包上。然後可以列舉對角線，然後再列舉對角線兩邊的點。當對角線定下來了以後，對於一側的三角形，可以發現它的面積是單峰的——三角形頂點沿一個方向移動的時候，面積先增後減。那麼當三角形面積開始減小的時候就可以停止枚舉了。這時候，我們就得到了此對角線下的最優解。

比如說這樣，這時我們的對角線是紅色的線段，藍色的四邊形就對應最優解。

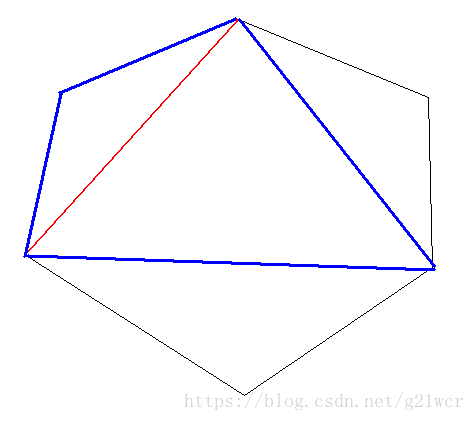
然後移動這個對角線的一個頂點。如下：

我們發現這時可以利用前一個的最優解！因為前面保證了是單增的。

然後就可以從前一個的最優解開始列舉，過程如下：

思想和旋轉卡殼類似。

#include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn=10000;
struct point{
    double x,y;
    point(double _x=0,double _y=0){x=_x,y=_y;}
    friend inline point operator +(const point &a,const point &b){
        return point(a.x+b.x,a.y+b.y);
    }
    friend inline point operator -(const point &a,const point &b){
        return point(a.x-b.x,a.y-b.y);
    }
    friend inline double operator *(const point &a,const point &b){
        return (a.x*b.y-a.y*b.x);
    }
}p[maxn],st[maxn];
double ang[maxn],ans=0,parta=0,partb=0;
int id=1,top=0,n;
inline double dist(point a,point b){
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
inline bool cmp(const point &a,const point &b){
    double K=(a-p[1])*(b-p[1]);
    return (K==0)?(dist(a,p[1])<dist(b,p[1])):(K>0);
}
inline int add(int a){return ((a+1)>top)? a+1-top : a+1;}
inline void Graham(){
    swap(p[id],p[1]);
    sort(p+2,p+n+1,cmp);
    st[++top]=p[1];
    for(int i=2;i<=n;++i){
        while((top>=3)&&((p[i]-st[top-1])*(st[top]-st[top-1])>=0))
            top--;
        st[++top]=p[i];
    }
    st[top+1]=st[1];
}

//i和j是對角線頂點，k和l是兩邊的頂點。
inline void rotating_calipers(){
	int i,j,k,l;
    for(i=1;i<=top;++i){
    	k=i,l=add(i);
	    for(j=i+1;j<=top;++j)
		{
			while((st[add(k)]-st[i])*(st[j]-st[i])>(st[k]-st[i])*(st[j]-st[i])) k=add(k);
			while((st[j]-st[i])*(st[add(l)]-st[i])>(st[j]-st[i])*(st[l]-st[i])) l=add(l);
			ans=max(ans,(st[j]-st[i])*(st[l]-st[i])+(st[k]-st[i])*(st[j]-st[i]));
		}
	}
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i){
        scanf("%lf%lf",&p[i].x,&p[i].y);
        if(p[i].y>p[id].y||((p[i].y==p[id].y)&&(p[i].x<p[id].x))) id=i;
    }
    Graham(),rotating_calipers();
    printf("%.3f\n",ans/2);
}