圖的遍歷

圖由頂點及其邊組成，圖的遍歷主要分為兩種：

1. 遍歷所有頂點
2. 遍歷所有邊

我們只討論第一種情況，即不重複的列出所有的頂點，主要有兩種策略：深度優先搜尋（DFS）,廣度優先搜尋（BFS）

為了使深度和廣度優先搜尋的實現演算法的機制更容易理解，假設提供了一個名為visit的函式，它負責處理每個單獨節點所需的任何處理。 因此，遍歷的目的是按照確定的連線順序在每個節點上呼叫且僅呼叫一次該函式。 因為圖形通常具有前往相同節點的許多不同路徑，所以確保遍歷演算法不會多次訪問同一節點我們需要額外的變數來跟蹤已經訪問過哪些節點。 為此，接下來的兩個部分中的實現定義了一組名為visited的節點，以跟蹤已經處理的節點。

• visit（） //對節點進行相應的操作
• visited //標記已訪問過的節點，可以用vector或者set，棧儲存都可以，這裡我們使用set來儲存
• foreach(A in B) 在A中搜索符合條件B的元素（遍歷）

深度優先搜尋（Depth-first search）

遍歷圖的深度優先策略類似於樹的前序遍歷，並具有相同的遞迴結構。 唯一的複雜因素是圖表可以包含環。 因此，必須跟蹤已經訪問過的節點。
下面的程式碼實現的是從某個特定的節點出發進行的深度優先搜尋。

/*
*資料結構 node
*說明：節點的資料結構、
/*
struct Node {
	string name; //節點名稱
	set<Arc *> arcs; //該節點的邊的集合
};
/*
*結構：Arc
*說明：邊的資料結構
*/
struct Arc {
	Node *start; //即從哪個節點出發
	Node *finish; //即指向哪個節點
	double cost;//邊的權重
};


* 函式 ：depthFirstSearch
* 用法: depthFirstSearch(node);
* ------------------------------
* 用指定的節點來初始化DFS的起始節點
*/
void depthFirstSearch(Node *node) {
	Set<Node *> visited;
	visitUsingDFS(node, visited);
}
/*
* 函式: visitUsingDFS
* 用法: visitUsingDFS(node, visited);
* ------------------------------------
* 從特定的節點執行DFS ，並避免重複遍歷相關節點
*/
void visitUsingDFS(Node *node, set<Node *> & visited) {
//如果在visited集合中存在該節點，說明為simple case，直接返回
	if (visited.contains(node)) return; 
	//否則
	visit(node);//對該節點進行相應操作
	visited.add(node);//將該節點新增到visited集合中
	foreach (Arc *arc in node->arcs) {
	//對每一個節點遞迴呼叫DFS演算法
		visitUsingDFS(arc->finish, visited);
	}
}
 

DFS的具體過程

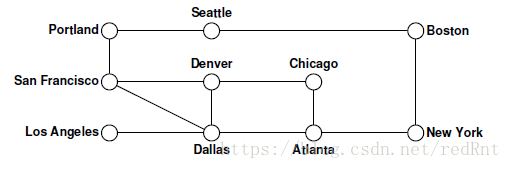
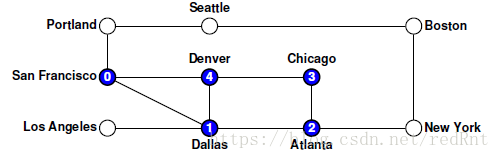
下面用一個例項來體會一下DFS的具體過程。還是上次的那張圖

節點被繪製為空心圓圈以指示它們尚未被訪問。 隨著演算法的進行，這些圓圈中的每一個都將標有記錄處理該節點的順序的數字。
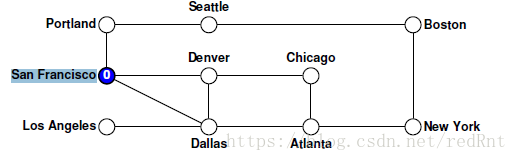
對depthFirstSearch函式本身的呼叫會建立一個空的set集合，然後將控制權移交給遞迴的visitUsingDFS函式。 假設我們的演算法從節點San Francisco處開始，該節點記錄在圖中，如下所示：

1. 對於該節點對應的每一條弧，都遞迴執行DFS演算法。

foreach (Arc *arc in node->arcs) {
	visitUsingDFS(arc->finish, visited);
}
 

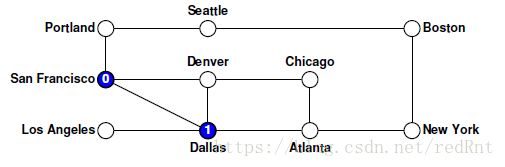
2. 這些呼叫發生的順序取決於foreach逐步遍歷弧的順序。 假設foreach按字母順序處理節點，因此優點選擇的是Dallas節點，迴圈的第一個迴圈呼叫visitUsingDFS和Dallas節點，所以會像下圖那樣：
   
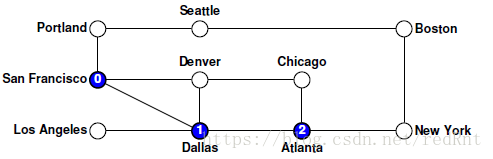
3. 根據我們的程式碼，我們必須在San Francisco尋找其他路徑時，完成對Dallas節點的DFS呼叫。因此根據我們假設的優先訪問規則，下一個要訪問的節點就是Atlanta
   
   深度優先搜尋演算法的總體效果是在回溯之前儘可能地探索圖中的單個路徑以完成對更高級別的路徑的探索。
4. 因此對於Atlanta節點而言，有兩個節點相鄰，我們根據字母表的優先，選擇Chicago節點。（因為此時的Dallas已經被標記，不在作為節點選擇參考的物件）。以此類推：
   
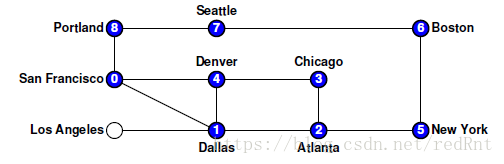
5. 然而，當程式走到Denver節點時，發現已經沒有可以走的路了，因為周圍的節點都被標記過，那麼只能往後回溯（就是後退），後退的第一個節點是Chicago，顯然情況跟Denver節點一樣，那麼繼續回溯，是Atlanta節點，發現該節點還有一條未被探索的路徑，所以它回溯到Atlanta節點後，選擇了New York節點，繼續執行DFS：
   
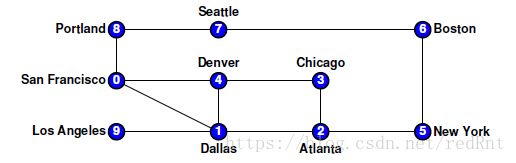
6. 同樣，以此類推，程式執行到Portland，開始回溯，一直到Dallas。（路徑顯然為8 -> 7 -> 6 -> 5 ->2）.發現Dallas還有未被探索的路徑。於是找到LosAngeles節點，繼續執行DFS。至此，圖中所有的節點都遍歷完畢：
   

當然我們可以更為方便的用棧來存放標記的元素，這樣我們可以在回溯的時候，將元素從棧中彈出即可。當棧空時即表明圖的遍歷完成，棧始終不空，表明圖中有一直不能訪問到的點，因為沒有路徑通過，此時圖為不連通的。

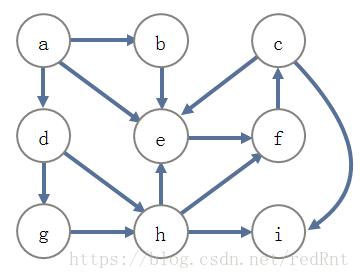
那麼同樣的對於下面的有向圖，也可以如下進行搜尋，如圖

假設從節點A開始用DFS演算法進行遍歷，使用棧來儲存標記過的節點，那麼具體如何實現呢？我會在接下來的博文中詳細分析。