機器學習 | 吳恩達機器學習第四周學習筆記
第四周課件 下載密碼:kx0q
上一篇部落格主要介紹了第三週的課程的內容,主要講解分類問題,引入了邏輯迴歸模型來解決分類問題,並詳細的介紹了邏輯迴歸模型的細節,包括假設函式,代價函式,優化求解方法包括之前學習的梯度下降法和更高階的優化方法,以及多分類問題的探討,最後介紹了過擬合問題,並以線性迴歸和邏輯迴歸為例講解該問題的解決方法(正則化)。本篇部落格將系統的介紹第四周的學習內容,本週主要講的是神經網路學習,包括非線性假設(通過例項說明邏輯迴歸解決分類問題的侷限性以及引入神經網路進行分類的必要性),神經元和大腦(神經網路演算法的由來),神經網路模型的表示以及工作原理,通過邏輯運算的例子直觀的理解神經網路,最後簡單介紹了利用神經網路進行多分類的問題。
目錄
神經網路學習
1.非線性假設
- 研究神經網路的目的
之前我們已經學習了線性迴歸和邏輯迴歸,對於大多數的分類或迴歸問題都有了一個不錯的解決方案,那麼我們為什麼還要學習神經網路呢?首先通過一個例子,闡述一下研究神經網路的目的:
下圖是一個數據集視覺化的結果,該資料集有兩個原始輸入特徵,現在要對該資料集的樣本進行一個二分類:
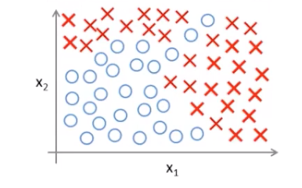
假設我們此時使用的是邏輯迴歸演算法,如果僅使用原始的兩個輸入特徵,是不可能把樣本分類好的,因為我們需要一個非線性的決策邊界。所以,此時我們應該在原始特徵的基礎上增加新的特徵,比如這些原始特徵的組合。決策邊界和假設函式如下所示:

通過對原始特徵進行組合增加特徵,相當於資料集此時有多個輸入特徵,可以把每一種原始特徵的組合當做一個新的輸入特徵。那麼我們就有可能得到一個非線性的決策邊界,從而如圖中所示,把這些樣本分開。
當只有兩個原始輸入特徵時,上述這種組合方法是可行的,大不了就把所有的原始特徵組合都包含到假設函式中。
但是,大多數機器學習問題的特徵數量都是很大的,考慮如下的房價資料集,他有

為了得到一個很好的分類效果,我們可能會對原始特徵進行組合以得到新的輸入特徵,接下來我們嘗試一些組合方式,來檢視特徵的增加量:

首先我們考慮所有原始輸入特徵的2次項組合,包括大約有5000個新特徵,此時特徵增加量級是
;
當然,對於2次項的組合,我們也可以做一些簡化,比如可以只取所有的平方項,那麼此時特徵會大大減少,只有100個。這不是一種好的做法,雖然特徵數減少了,但是忽律了太多特徵細節,很有可能得不到一個理想的分類效果。
既然有2次項組合,那麼肯定可以進行3次項的組合,包括等大約有170000個新特徵,此時特徵增加量級是
。
當然還有各種原始特徵組合方式,但是當進行到3次項組合時,我們發現特徵數量就已經非常多,而這僅僅是在原始特徵數為100個的情況下。那麼當原始特徵更多時,可想而知,此時的特徵空間會極度膨脹。接下來我們看另一個例子:

這是一個計算機視覺的問題,我們的目的是讓計算機看懂這張圖片代表的是什麼。當然對於我們人來說,這很簡單,就是一輛車;但對於計算機來說卻很難,他看到的實際是一個畫素矩陣,矩陣中的元素是畫素的亮度值。計算機視覺就是根據矩陣中畫素的亮度值,得到他的含義,代表的是什麼東西。

上圖是一個汽車分類的問題,我們再對汽車進行分類時,首先需要一個標註訓練資料集,包含一些汽車圖片和一些非汽車圖片,然後我們用這個標註資料集訓練我們的分類模型,訓練結束後,再進行測試,通過輸入一張新的圖片,讓之前訓練好的分類器判斷它是什麼。

假設我們在一幅汽車圖片上取兩個畫素點作為原始輸入特徵,那麼可能會得到這樣一個數據集,我們把它視覺化,其中+代表汽車,-代表非汽車:

很顯然我們需要一個非線性的決策邊界。實際上,對於一幅汽車圖片,它遠遠不止兩個畫素點。假設我們的汽車圖片,畫素是50*50的灰度圖,那麼它就有2500個畫素點(每個畫素點亮度取值0-255),也就意味著有2500個原始輸入特徵;如果考慮彩色圖的話,會有RGB三個顏色通道,此時將會有7500個原始輸入特徵。
如果我們再像之前那樣,通過對原始特徵進行組合,增加新特徵的話,僅僅是2次項組合方式,就會增加300w個新特徵,這是相當恐怖的,更不用說其他組合方式了。

因此,通過上述兩個例子,我們知道在原始輸入特徵很多的情況下,再使用簡單的邏輯迴歸並通過對原始特徵組合增加新特徵的方式是不可行的,計算成本太高。
我們此時需要一個更加強大的非線性分類器--神經網路,與邏輯迴歸不同,不論原始輸入特徵是多少維,它都會有一個很好的分類效果。
2.神經元與大腦
神經網路的起源是一種模仿人類大腦的演算法。
既然我們想要創造一個智慧的機器,我們何不模仿人類最神奇的大腦,如果我們知道了大腦的學習演算法,那麼我們就能製造出真正智慧的機器了。而這個假設是有科學依據的:

圖中所示的大腦皮層是我們的聽覺皮層,如果我們切斷聽覺神經併為聽覺皮層連線上視覺神經,我們會發現這個聽覺皮層會學會看。
這就說明,大腦會根據我們看到的事物,通過一種學習演算法,從而得到一種看的能力。我們致力於研究的正是這種學習演算法。一旦知道了該演算法的機理,那麼真正的智慧就會誕生了。
3.模型展示I
本小節我們將學習如何表示神經網路:
首先我們先看一下大腦中的神經元結構:

神經元通過Dendrite(輸入通道)接收資訊,再通過Nucleus(細胞體)處理資訊,最後通過Axon(輸出通道)將處理後的資訊傳遞給其他神經元。
接下來我們使用人工神經網路模型來模仿大腦的神經元:
- 單個神經元

僅考慮存在三個輸入特徵,事實上可以有個輸入特徵。
單個神經元的模型實際上完全可以看作是一個邏輯迴歸模型,原始輸入特徵稱為輸入層;圖中的黃圈代表神經元,稱為輸出層;
是模型最後的輸出,
.
神經元的計算操作,就是對原始輸入特徵進行加權組合,再通過一個sigmoid啟用函式,得到最後的輸出。其中是引數,也叫權重,
是原始輸入特徵。
有時候會在輸入特徵中增加一個偏置項,其值恆等於1;有時候則沒有該項,視具體情況而定。
- 多個神經元

其中Layer1稱為輸入層,對應原始輸入特徵,可以有個,有時需要新增一個偏置項
;
Layer3為輸出層,上圖中只有一個神經元,實際上可以有多個,視情況而定(幾分類就有幾個);
Layer2為隱藏層,上圖中只有一個隱藏層,實際上隱藏層可以有多個,輸入層和輸出層之間的都是隱藏層;而且每個隱藏層可以有多個神經元,有時隱藏層也會有偏置項。
各層之間的神經元採用全聯接的方式。
接下來看一下各層之間具體的運算過程和符號表示:

:第j層的第i個神經元
:從第j層到第j+1層的權重(引數)矩陣,如果第j層有
個神經元,第j+1層有
個神經元,那麼他們之間的權重矩陣
的維度是
.
具體的運算過程如上圖所示,前一層所有神經元輸出值的加權組合再通過一個sigmoid啟用函式,作為下一層每一個神經元的輸入。
上圖中的網路結構比較簡單,實際上一般有很多隱藏層,每個隱藏層有很多神經元,計算過程都是一樣的。
輸入層的單元數由原始輸入特徵決定。
輸出層的單元數由分類類別數決定。
總結:
神經網路實際上可以得到一個從輸入特徵x到輸出變數y的一個對映.根據引數
的不同,就會得到不同假設函式
。
4.模型展示II
- 向量化表示方法:

用向量表示所有輸入原始輸入特徵+偏置項,它的每一維度代表一個原始輸入特徵,
也可以記為
。
向量與第j層的神經元有關,每個分量代表j-1層特徵的加權組合。
向量是
經過啟用函式得到的結果,兩個向量是同維的;
是第j層神經元的輸出。
對新增偏置項
,作為j+1層的輸入,重複上述過程,直到輸出層得到假設函式
。
上述過程就是神經網路演算法的前向傳播過程,從輸入層開始,上一層的特徵向量作為輸入和一個引數矩陣進行線性組合,再通過一個啟用函式,最後新增一個偏置項,得到下一層的輸出;該輸出再作為下一層的輸入重複上述過程,直到輸出層。
- 神經網路原理

如果我們遮住左半邊只看上圖中的黃色部分,實際上它就是一個邏輯迴歸,對輸入特徵進行加權組合,再通過sigmoid,得到。
但是神經網路的不同在於,他不是直接以原始輸入特徵作為輸入,而是先對原始輸入特徵通過隱藏層進行一系列訓練,計算出更復雜的特徵,來作為最終“邏輯迴歸”的輸入,從而得到一個複雜的非線性假設。
這些複雜的特徵取決於權重,
不同,計算得到的複雜特徵也就不同。
輸入層一般來說是原始特徵,當然也可以對原始特徵進行一些組合,形成新的特徵;二者拼接作為輸入層,也是可以的。
- 其他結構神經網路

Layer1是原始輸入特徵;
Layer2是對原始輸入特徵進行計算得到複雜特徵1;
Layer3再對複雜特徵1進行計算得到複雜特徵2;
複雜特徵2最後作為“邏輯迴歸”的輸入特徵,進行分類(上圖是2分類)。
隱藏層越多,計算得到的特徵就越複雜,就會得到更加複雜的非線性假設和決策邊界。
5.例子與直覺理解I
簡單邏輯運算:
- AND

假設權重已經訓練得到,分別是,那麼假設函式
也就確定了,表示式如上圖中所示。
上圖是單神經元結構,g是sigmoid啟用函式,對於不同的輸入組合,帶入
,得到最終的結果,如上圖所示。
- OR

假設權重已經訓練得到,分別是,那麼假設函式
也就確定了,表示式如上圖中所示。
上圖是單神經元結構,g是sigmoid啟用函式,對於不同的輸入組合,帶入
,得到最終的結果,如上圖所示。
6.例子與直覺理解II
- NOT

假設權重已經訓練得到,分別是,那麼假設函式
也就確定了,表示式如上圖中所示。
上圖是單神經元結構,g是sigmoid啟用函式,對於不同的輸入,帶入
,得到最終的結果,如上圖所示。
- 複雜邏輯運算XNOR
可以把簡單的邏輯運算複合在一起:
XNOR
= (
AND
) OR ((NOT
) AND (NOT
))

假設簡單邏輯運算的權重已經訓練得到,分別如上圖所示,下半部分的複雜邏輯運算可以直接用各簡單邏輯運算的引數,那麼假設函式也就確定了。
上圖是多神經元結構,除了輸入、輸出層之外還有一個隱藏層,隱藏層對輸入層的特徵進行計算,得到更復雜的特徵,從而得到一個複雜的非線性決策邊界,使用的是sigmoid啟用函式,對於不同的輸入組合,帶入上圖中的結構,得到的隱藏層結果和最終的結果,如上圖所示。
7.多元分類
實際中,我們一般用神經網路解決一些多類別分類的問題。
首先我們來看一個四分類的例子,他的訓練資料集如下:

其中是原始輸入特徵,
為輸出變數(標記Label);由於這是一個四分類問題,
是一個四維向量,且只有一個分量為1,代表該訓練樣本所屬的類別,具體類別對應如上圖所示。
採用的神經網路結構:

假設採用的神經網路結構如上圖所示,它有四層,輸入層有三個單位,代表原始輸入特徵是3維的;輸出層有四個單元,代表進行一個四分類;中間有兩個隱藏層,用於對原始特徵進行訓練,得到更加複雜的特徵,從而最後得到複雜的非線性決策邊界。
- 訓練過程:
首先初始化模型引數,把所有的訓練樣本“喂”給上述網路模型,通過前向傳播,到輸出層得到一個四維向量,對該向量進行歸一化操作(softmax),再與訓練樣本標籤y計算損失函式;
最小化該損失函式,反向傳播(下節講述)更新模型引數,直到得到一組不錯的模型引數為止,模型訓練結束。
- 測試過程:
模型訓練結束後,引數也就確定了,對於新的樣本,將其輸入特徵帶入上述網路結構中,得到最後的輸出並歸一化,得到一個四維向量,該向量哪個分量的數值最大,則認為這個新樣本屬於哪個類別。

8.程式設計作業:多元分類與神經網路
本週的程式設計作業詳見我的另一篇部落格:神經網路與多分類
