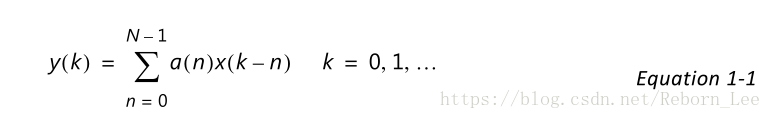【 FPGA 】SMAC(脈動型乘累加結構)FIR濾波器總結
先貼出來傳統的FIR濾波器實現結構作為後面的對比:
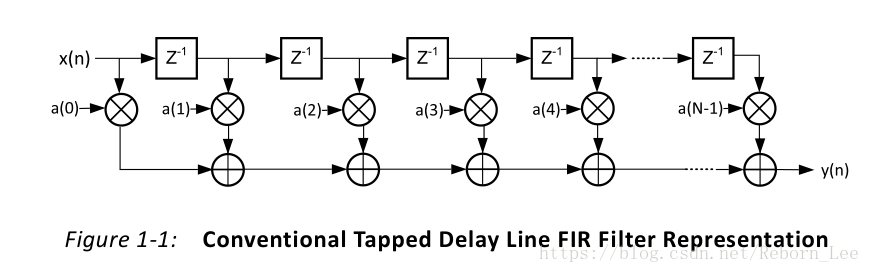
傳統的FIR濾波器的實現結構:
(【 FPGA 】FIR濾波器開篇之傳統抽頭延遲線FIR濾波器實現介紹)
圖1
實現公式如下:
上面貼出的博文也說了,這種結構對於概念的理解很有幫助,但是實際的FPGA實現不用!
我們以10階的FIR濾波器為例,也就是有11個係數(抽頭),那麼它的輸出就是上式的N改為11即可。也即:
(1)
這裡提前宣告下,由於圖片來源不同,所以為了統一符號,這裡的h(n)和a(n)都一樣,都表示濾波器的係數,也就是抽數代表的數值。
相關博文:【 FPGA 】FIR 濾波器的架構
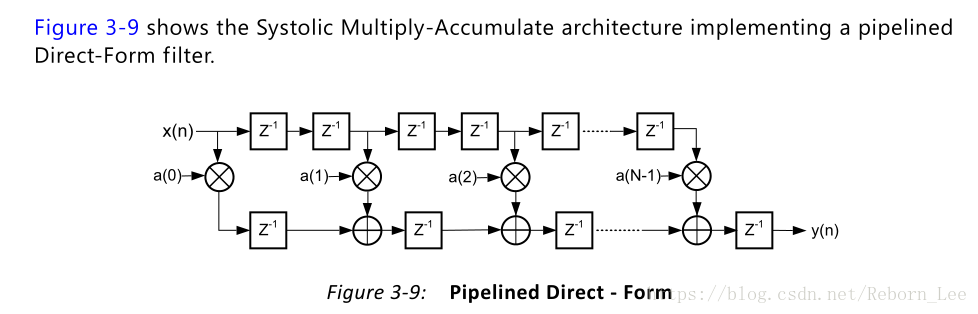
下面是脈衝型乘累加結構的FIR濾波器的一種形式,可稱為流水線直接型,脈動型乘累加結構簡寫為SMAC結構,英文名:Systolic Multiply-Accumulate(SMAC)。
這個詞:Systolic,英文翻譯為收縮,脈動等,那如何理解呢?
我看到了這樣的一句話,僅供參考:脈動型FIR濾波器是對直接型的升級,在每個操作後都加入流水線級,每個動作都打一拍,就跟心臟跳動一樣,因此稱為脈動型,這種結構非常適用於高速資料流的處理。
這句話來源:(http://my.bj51.org/article/id/13902)
下面通過公式推導,看看這種結構是如何實現FIR濾波器的。

圖2
上圖(網上資源)與下圖(Xilinx官方資料手冊)等價:
圖3
以圖二為例:(手稿)
與直接型結構不同的是,輸入資料到下一個處理單元都需要打2拍,這是為了使乘法後的累加資料同步,下面是驗證過程:
(天天用鍵盤,突然手寫,感覺好艱難,不過也好過敲公式。)
可見,使用這種SMAC結構的FIR濾波器可以實現傳統濾波器的功能,只不過有點延遲而已。
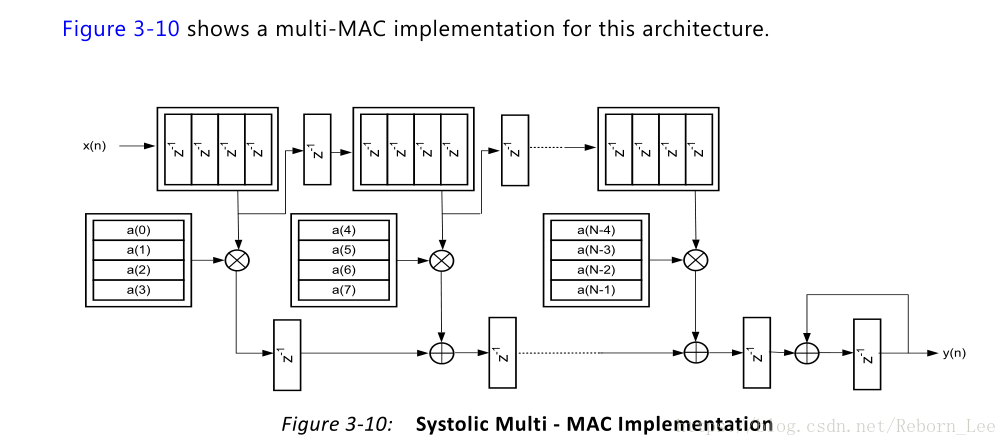
那又有一個問題是FPGA是不是就是用這種結構的呢?那還不一定,因為資料手冊上給出了多MAC實現的SMAC架構,如下圖:
博文:FIR濾波器架構
圖4
這種多MAC的SMAC架構的實現,我還沒看懂,不便分析。
在博文:【 FPGA 】FIR濾波器的取樣速率與系統時鐘速率不同時的資源消耗分析
在定製FIR濾波器的IP核的分析中,採用SMAC結構,發現在FPGA中消耗的資源是DSP slice,如下(選取了任意一張圖):
圖5
為什麼消耗的是DSP slice資源呢?博文中也作出了簡單的分析,資料手冊中有直接的答案,那就是該SMAC結構直接由DSP片支援,從而實現了區域高效和高效能的過濾器實現。
由此,我們過渡到下圖:

圖6
該圖也來自網際網路,還有下面這段話:
圖6所示為11抽頭係數脈動型FIR濾波器FPGA實現結構(例項與前幾節相同),穿了一層“衣服”,採用Xilinx FPGA中的DSP48E1 實現,基本處理單元中的操作都可在一個DSP48E1中完成,輸入資料經過DSP48E1中寄存2拍後通過ACOUT輸出,直接連線到下一個 DSP48E1中的ACIN埠,累加輸出PCOUT直接連線到下一個DSP48E1中的PCIN埠,這些連線都沒有經過FPGA的Fabric連線邏輯,而是通過DSP Block的內部走線連線,這樣實現能夠縮短路徑的延時。
這段話來源:http://my.bj51.org/article/id/13902(下面的這種情況也是來源於此地址)
下圖是通過線性相位實現的SMAC結構:

圖7
如圖7所示,各節點P1、P2、P3、P4、P5和y(n)的表示式如下
P1=x(n-5)h(0) + x(n-15)h(0)
P2=( P1 + (x(n-6)h(1) + x(n-14)h(1)) )Z-1=x(n-6)h(0) + x(n-16)h(0) + x(n-7)h(1) + x(n-15)h(1)
P3=( P2 + (x(n-8)h(2) + x(n-14)h(2)) )Z-1=x(n-7)h(0) + x(n-17)h(0) + x(n-8)h(1) + x(n-16)h(1) + x(n-9)h(2) + x(n-15)h(2)
P4=( P3 + (x(n-10)h(3) + x(n-14)h(3)) )Z-1=x(n-8)h(0) + x(n-18)h(0) + x(n-9)h(1) + x(n-17)h(1) + x(n-10)h(2) + x(n-16)h(2) + x(n-11)h(3) + x(n-15)h(3)
P5=( P4 + (x(n-12)h(4) + x(n-14)h(4)) )Z-1=x(n-9)h(0) + x(n-19)h(0) + x(n-10)h(1) + x(n-18)h(1) + x(n-11)h(2) + x(n-17)h(2) + x(n-12)h(3) + x(n-16)h(3) + x(n-13)h(4) + x(n-15)h(4)
y(n)=(P5 + x(n-14)h(5))Z-1= x(n-10)h(0) + x(n-20)h(0) + x(n-11)h(1) + x(n-19)h(1) + x(n-12)h(2) + x(n-18)h(2) + x(n-13)h(3) + x(n-17)h(3) + x(n-14)h(4) + x(n-16)h(4) + x(n-15)h(5)
因抽頭係數對稱,由h(0)=h(10),h(1)=h(9),h(2)=h(8),h(3)=h(7),h(4)=h(6)可得
y(n)= x(n-10)h(0) + x(n-11)h(1) + x(n-12)h(2) + x(n-13)h(3) + x(n-14)h(4) + x(n-15)h(5) + x(n-16)h(6) + x(n-17)h(7) + x(n-18)h(8) + x(n-19)h(9) + x(n-20)h(10)
驗證得到y(n)=yt(n-10),比普通脈動結構延時小,但是相比於其他結構的FIR濾波器延時還是較大的。
這是係數對稱的情況,可以這麼實現,如果係數不對稱,恐怕就沒有這麼個對比了。
如果使用IP compiler去設計一個SMAC結構的FIR濾波器,其內容具體使用那種結構,那就不知道了,只能說大概就是如此。
寫到這裡,似乎還是不滿意。因為對它的時序關係還不是太瞭解。那下篇博文是不是應該分析下時序問題呢?我去看看再說!