1. 氣泡排序

思路：

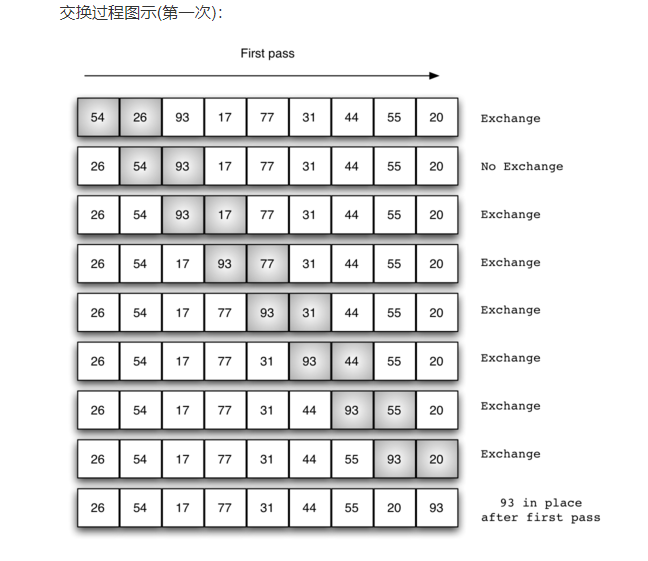
可以看做按對高低不一的一組學生按照大小個排隊，校長從每次從頭開始走，觀察當前站的位置與後一個位置元素大小進行比較，如果比當前元素大，就交換兩者的位置，然後往後走一步，接著比較當前元素與後一個位置元素大小，重複剛才的過程，，，校長一次從頭走到尾的遍歷過程最大位置的元素跟著走到了最後，第二次遍歷，佇列中第二大的元素走到了倒數第二個位置，，，以此類推；

2. 程式碼實現（python）

def bubble_sort(L):
    """氣泡排序"""
    n=len(L)
    for i in range(n-1):  # 校長從頭走到尾的過程持續進行了n-1次
 

        for j in range(n-1-i):  # 校長在一次遍歷中需要從頭走到尾，比較當前位置元素與下一個元素的大小，最終把最大的元素安排到最後一個位置
            if L[j]>L[j+1]:
                L[j],L[j+1]=L[j+1],L[j]
    return L
print(bubble_sort([2,6,1,3,8,4,7,0,9]))

執行結果：

 3. 時間複雜度

氣泡排序的時間複雜度是O(n^2)----因為包含兩個for 迴圈；

4. 穩定性

穩定性： 氣泡排序是穩定的，被排序的陣列中出現兩個相同的元素時，氣泡排序會維持兩者原來的相對順序，所以是穩定的

 5. 優化

我們發現當陣列原本就是有序序列，使用剛才的實現複雜度仍然是O(n^2) ，其實我們可以對它進行改進，就是當校長從頭走到尾，發現並沒有發生元素的交換過程，就代表序列已經是有序的，就不需要再重複進行從頭走到尾的遍歷工作了；

def bubble_sort(L):
    """氣泡排序"""
    n=len(L)
    for i in range(n-1):  # 校長從頭走到尾的過程持續進行了n-1次
        count=0
        for j in range(n-1-i):  # 校長在一次遍歷中需要從頭走到尾，比較當前位置元素與下一個元素的大小，最終把最大的元素安排到最後一個位置
 

            if L[j]>L[j+1]:
                L[j],L[j+1]=L[j+1],L[j]
                count+=1
        if count==0:  # 如果從頭走到尾的某次過程未發生元素的交換，那麼被排序的序列已經是有序的~ 直接跳出迴圈即可
            break
    return L
print(bubble_sort([2,6,1,3,8,4,7,0,9]))

 這樣對有序序列的時間複雜度就變為O(n);