已知二叉樹的先序遍歷和中序遍歷畫出該二叉樹
對一棵二叉樹進行遍歷,我們可以採取3中順序進行遍歷,分別是前序遍歷、中序遍歷和後序遍歷。
這三種方式是以訪問父節點的順序來進行命名的。
假設父節點是N,左節點是L,右節點是R,那麼對應的訪問遍歷順序如下:
- 前序遍歷 N->L->R
- 中序遍歷 L->N->R
- 後序遍歷 L->R->N
所以,對於以下這棵樹,三種遍歷方式的結果是
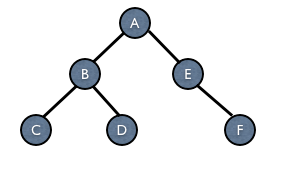
- 前序遍歷 ABCDEF
- 中序遍歷 CBDAEF
- 後序遍歷 CDBFEA
已知二叉樹的前序遍歷和中序遍歷,如何得到它的後序遍歷
其實,只要知道其中任意兩種遍歷的順序,我們就可以推斷出剩下的一種遍歷方式的順序,這裡我們只是以:
知道前序遍歷和中序遍歷,推斷後序遍歷作為例子,其他組合方式原理是一樣的。要完成這個任務,我們首先要利用以下幾個特性:
特性A,對於前序遍歷,第一個肯定是根節點;
特性B,對於後序遍歷,最後一個肯定是根節點;
特性C,利用前序或後序遍歷,確定根節點,在中序遍歷中,根節點的兩邊就可以分出左子樹和右子樹;
特性D,對左子樹和右子樹分別做前面3點的分析和拆分,相當於做遞迴,我們就可以重建出完整的二叉樹;
我們以一個例子做一下這個過程,假設:
前序遍歷的順序是: CABGHEDF
中序遍歷的順序是: GHBACDEF
第一步,我們根據特性A,可以得知根節點是C,然後,根據特性C,我們知道左子樹是:GHBA,右子樹是:DEF。
C
/ \
GHBA DEF
第二步,取出左子樹,左子樹的前序遍歷是:ABGH,中序遍歷是:GHBA,根據特性A和C,得出左子樹的父節點是A,並且A沒有右子樹。
C
/ \
A DEF
/
GBH
第三步,使用同樣的方法,前序是BGH,中序是GHB,得出父節點是B,GH是左子樹,沒有右子樹。
C
/ \
A DEF
/
B
/
GH
第四步,前序是GH, 中序是GH, 所以 G是父節點, H是右子樹, 沒有左子樹.
C
/ \
A DEF
/
B
/
G
\
H
第四步,回到右子樹,它的前序是EDF,中序是DEF,依然根據特性A和C,得出父節點是E,左右節點是D和F。
C
/ \
A E
/ / \
B D F
/
G
\
H
到此,我們得到了這棵完整的二叉樹,因此,它的後序遍歷就是 : HGBADFEC
