20172303 2018-2019-1《程式設計與資料結構》第5周學習總結
阿新 • • 發佈:2018-11-11
20172303 2018-2019-1《程式設計與資料結構》第5周學習總結
教材學習內容總結
終於結束了各種不同型別的資料結構的學習,本章的內容轉向了對於不同資料結構中儲存的資料的處理方面,主要學習了兩部分內容——查詢和排序,其中查詢介紹了兩種方法,排序除上學期學過的兩種排序方法,又學習了四種新的排序方法。
一、靜態方法
- 靜態方法:使用時不需要例項化該類的一個物件,可以直接通過類名來啟用的方法。可以通過在方法宣告中使用static修飾符將方法宣告為靜態的。
- 泛型方法:在方法頭的返回型別中有泛型宣告的方法。
public class MathTest { public static void main(String[] args) { MathTest mathTest = new MathTest(); System.out.println(mathTest.max(1, 2)); System.out.println(mathTest.max(2.0, 3.0)); } //泛型方法 private <T extends Comparable> T max(T t1, T t2) { return t1.compareTo(t2) > 0 ? t1 : t2; } //靜態泛型方法 private static <T extends Comparable> T max(T t1, T t2) { return t1.compareTo(t2) > 0 ? t1 : t2; } }
二、查詢
- 定義:在某個專案組(查詢池)中尋找某一指定元素目標或確定某一指定元素目標不在專案組中。
- 目標:儘可能高效地完成查詢——使過程中所做的比較次數最小化。
- 決定比較次數的因素:查詢的方法,查詢池中元素的數目。
1.線性查詢
- 概念:在一個元素型別相同的專案組中,從頭開始依次比較每一個值直至結尾,若找到指定元素返回索引值,否則返回false。
- 時間複雜度分析:最好的情況下是列表的第一個元素就是所要找的指定元素,此時的時間複雜度為O(1)。最壞的情況下,所找元素並不在列表中,那麼就需要遍歷列表直至尾部終止,這時要進行n次比較,時間複雜度為O(n)。所以,線性查詢的平均時間複雜度為O(n)。
2.二分查詢
- 概念:在一個已排序的專案組中,從列表的中間開始查詢,如果中間元素不是要找的指定元素,則削減一半查詢池,從剩餘一半的查詢池(可行候選項)中繼續以與之前相同的方式進行查詢,多次迴圈直至找到目標元素或確定目標元素不在查詢池中。
- 特點:二分查詢的每次比較都會刪除一半的元素。
- 時間複雜度分析:最好的情況是所要查詢的元素就位於查詢池的中央,此時的時間複雜度為O(1)。當所查詢元素不在查詢池中時,需要一直削減專案組的一半直至專案組的元素只剩下一個,這種情況下要進行log2n次比較。所以,二分查詢的平均時間複雜度為O(log2n)。
3.兩種查詢方法的比較
- 在元素個數較小時,兩種方法的效率幾乎沒有區別,但是當元素個數非常多時,二分查詢要優於線性查詢。
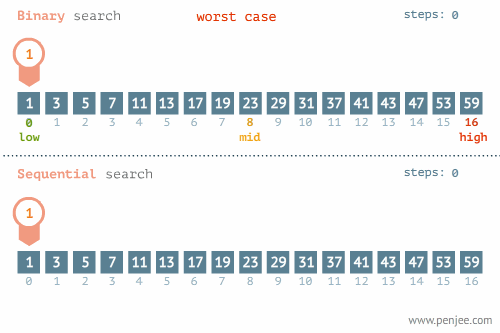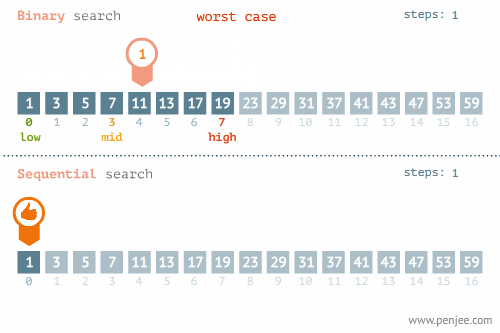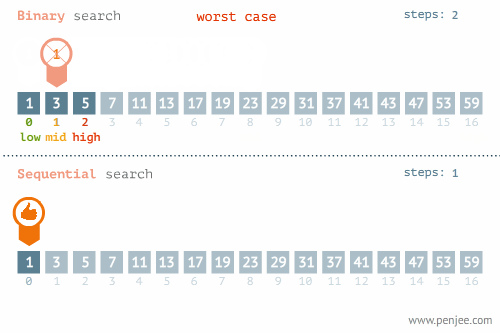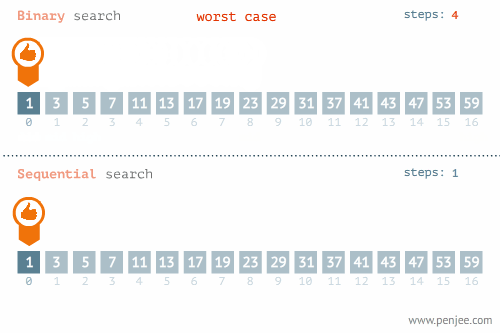
- 所找元素位置的不同也會影響查詢方法的選擇,比如在下面這個例子中,當使用線性檢索和二分檢索求23的位置和檢索1的位置時,二者的時間存在差別很大。
- 使用線性檢索和二分檢索求23的位置
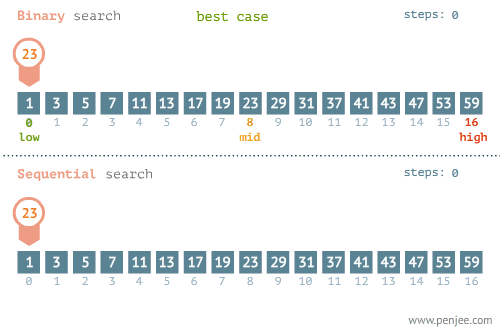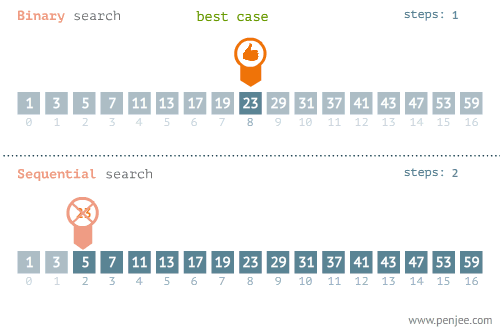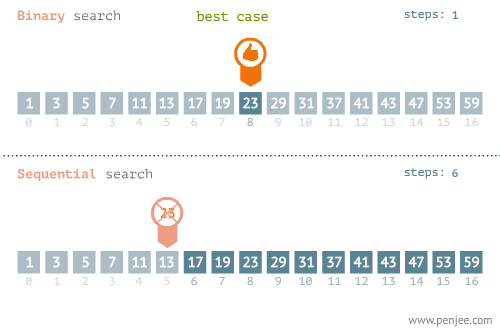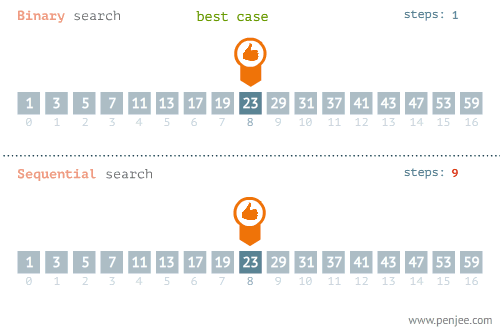
- 使用線性檢索和二分檢索求1的位置
三、排序
- 概念:基於某一標準,將某一組專案按照某個規定順序排序。
- 分類:順序排序(大概需要n^2次比較)對數排序(大概需要nlog2n次比較)
- 順序排序——選擇排序、插入排序、氣泡排序
- 對數排序——快速排序、歸併排序
- 基數排序
三種順序排序的時間複雜度均為O(n^2),原因是它們都要通過兩層迴圈來實現,且每層迴圈都要進行n次,下面主要進行兩層迴圈作用的分析。
1.選擇排序
- 原理:通過反覆將某一特定值放到它在列表中的最終已排序位置來實現排序。
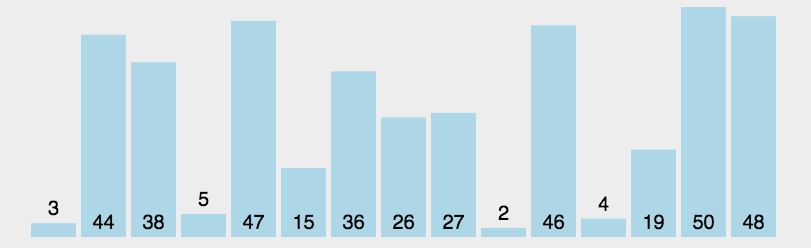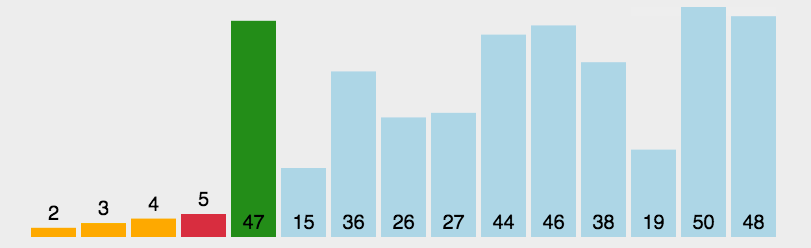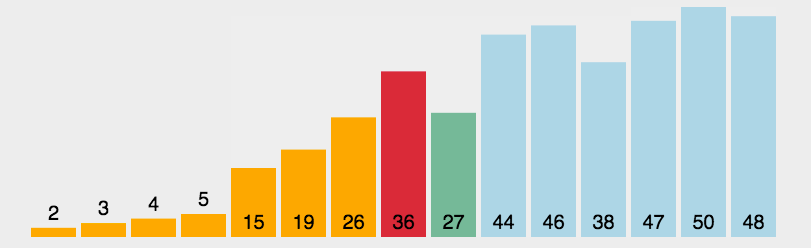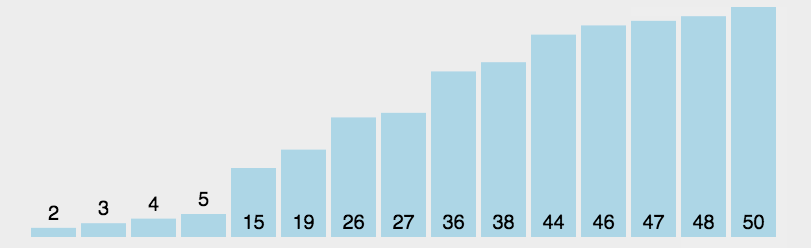
- 程式碼分析:選擇排序有兩層迴圈,外側迴圈控制下一個最值在列表中的儲存位置,內側迴圈通過遍歷和比較來找出剩餘列表的最值。
public static <T extends Comparable<T>> void selectionSort(T[] data)
{
int min;
T temp;
//迴圈次數為n,時間複雜度為O(n)
for (int index = 0; index < data.length-1; index++)
{
min = index;
//迴圈次數為n,時間複雜度為O(n)
for (int scan = index+1; scan < data.length; scan++) {
if (data[scan].compareTo(data[min])<0) {
min = scan;
}
}
swap(data, min, index);
}
}2.插入排序
- 原理:通過反覆將一特定值插入列表中某一已排序的自己中來實現排序。
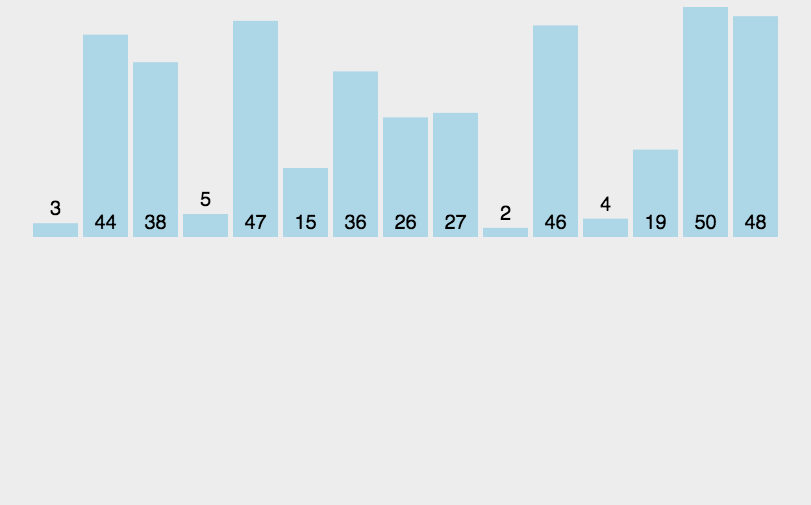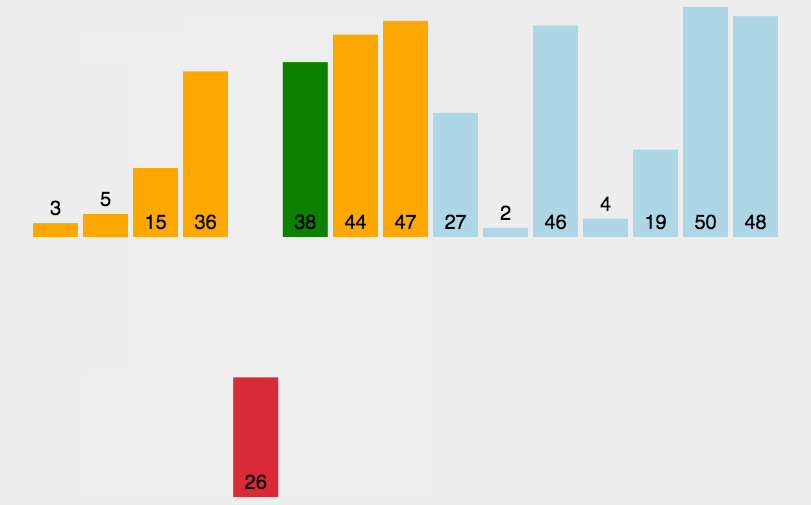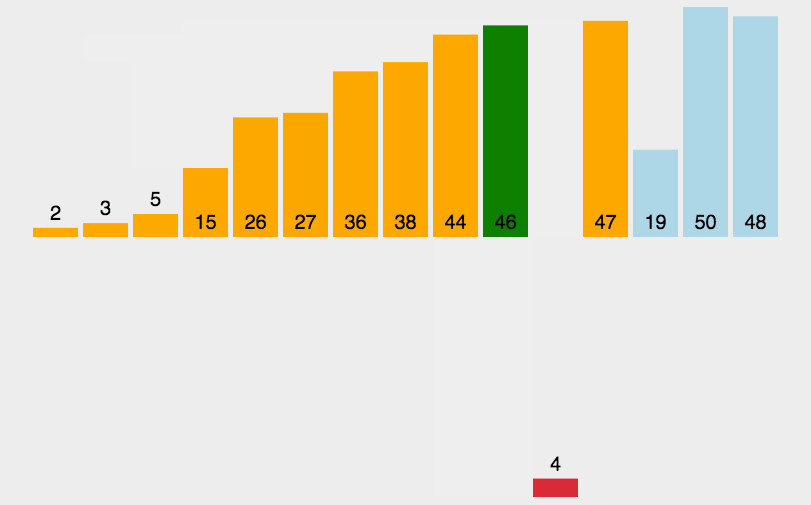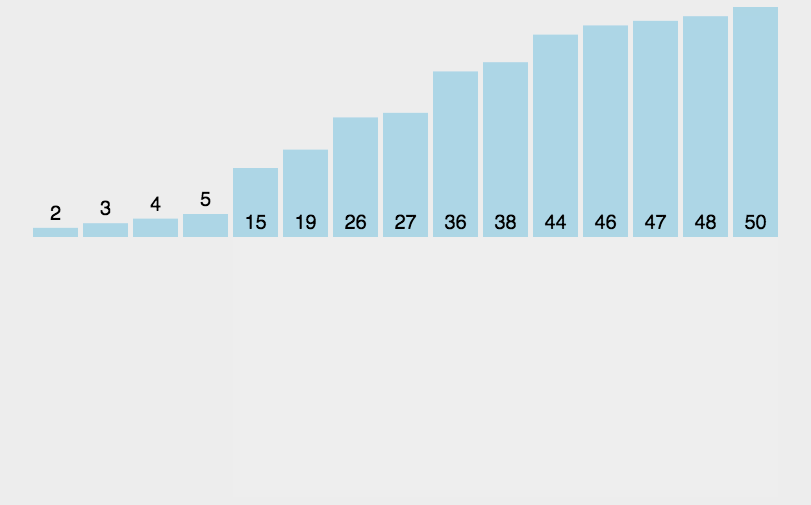
- 程式碼分析:與選擇排序類似,插入排序也使用了兩層迴圈,外側控制的是下一個插入值在列表中的位置,內側迴圈是將當前插入值與已排序子集中的值進行比較,兩者同樣都要迴圈n次。
public static <T extends Comparable<T>> void insertionSort(T[] data)
{
//迴圈次數為n,時間複雜度為O(n)
for (int index = 1; index < data.length; index++)
{
T key = data[index];
int position = index;
//迴圈次數為n,時間複雜度為O(n)
while (position > 0 && data[position-1].compareTo(key) > 0)
{
data[position] = data[position-1];
position--;
}
data[position] = key;
}
}3.氣泡排序
- 原理:通過反覆比較相鄰元素的大小並在必要時進行互換,最終實現排序。
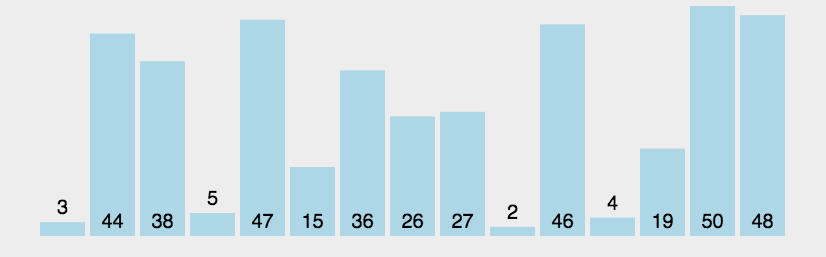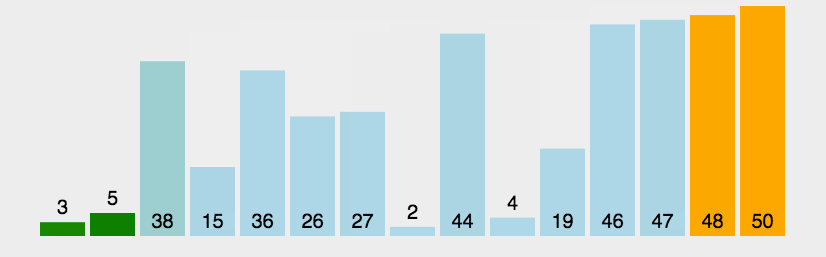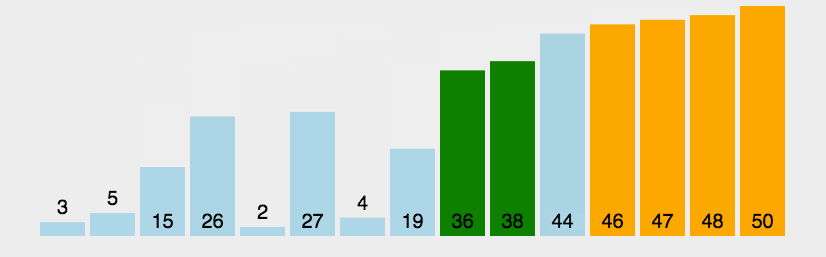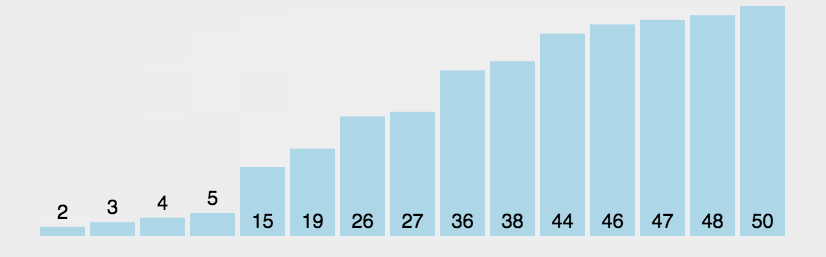
- 程式碼分析:氣泡排序的兩層迴圈中,外層迴圈負責不斷進行遍歷剩餘所有列表(共n-1次),內層迴圈在每次外層迴圈的過程中掃描所有相鄰元素並依據規則對他們進行互換。
public static <T extends Comparable<T>> void bubbleSort(T[] data)
{
int position, scan;
T temp;
//迴圈次數為n,時間複雜度為O(n)
for (position = data.length - 1; position >= 0; position--)
{
//迴圈次數為n,時間複雜度為O(n)
for (scan = 0; scan <= position - 1; scan++)
{
if (data[scan].compareTo(data[scan+1]) > 0) {
swap(data, scan, scan + 1);
}
}
}
}快速排序和歸併排序的平均時間複雜度相同,都是O(nlogn)。
4.快速排序
- 原理:通過將列表進行分割槽,對兩個分割槽內的資料進行遞迴式排序。
- 遞迴:用一句簡單易懂的話來講就是——自己呼叫自己。
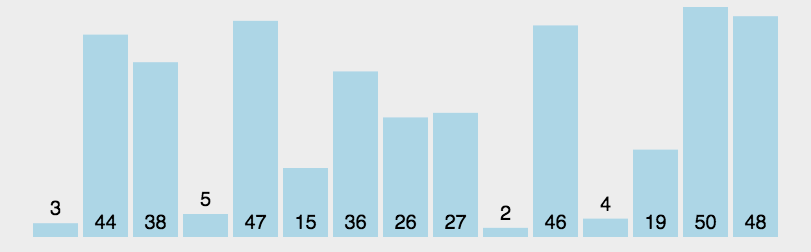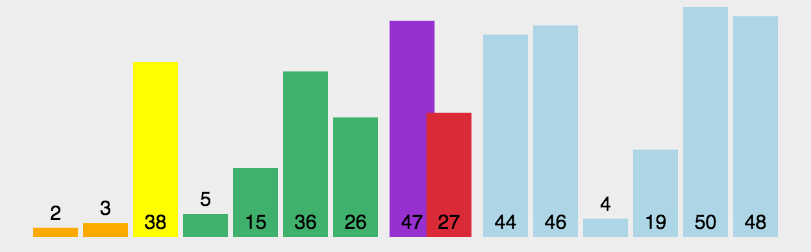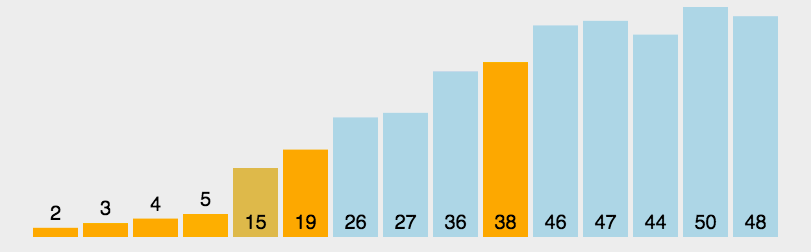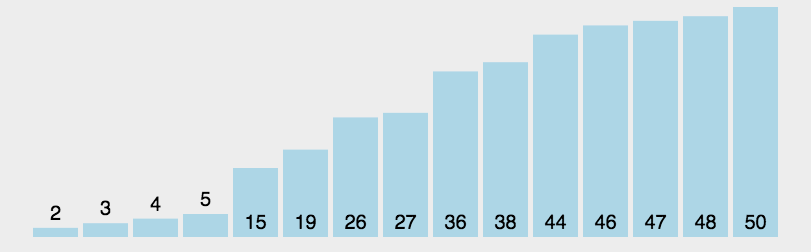
- 遞迴:用一句簡單易懂的話來講就是——自己呼叫自己。
- 程式碼分析:快速排序本身的程式碼實現非常簡單,就是一個遞迴的實現。但它其中最核心的方法是使用了一個分割槽方法
partition。- 該方法有兩層迴圈,外層迴圈負責進行每次分割槽的選擇,內層迴圈中有兩個
while迴圈,用於將兩個分割槽中對應位置錯誤的元素找到並進行交換,直至左索引與右索引相等。
- 該方法有兩層迴圈,外層迴圈負責進行每次分割槽的選擇,內層迴圈中有兩個
- 時間複雜度分析:快速排序每次要將列表分成兩個分割槽,因此平均要進行log2n次分割槽,而每次分割槽後要進行n次比較操作,因此平均時間複雜度為O(nlogn)。快速排序比大部分排序演算法都要快,但快速排序是一個非常不穩定的排序,因為若初始序列按關鍵碼有序或基本有序時,快速排序反而蛻化為氣泡排序,此時它的時間複雜度就為O(n^2)了。
5.歸併排序
- 原理:通過將列表進行遞迴式分割槽直至最後每個列表中都只剩餘一個元素後,將所有列表重新按順序重組完成排序。
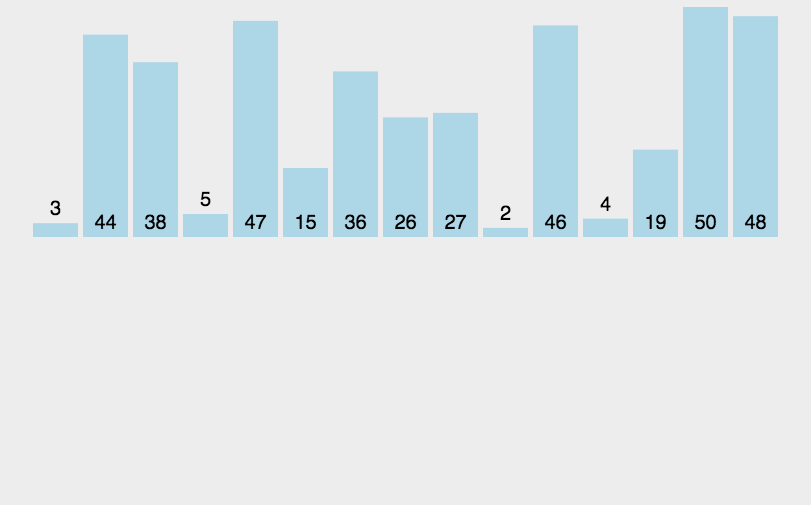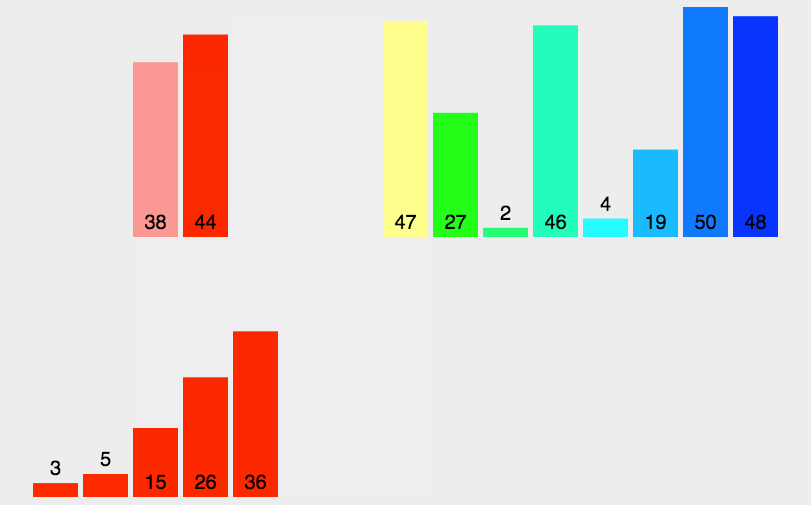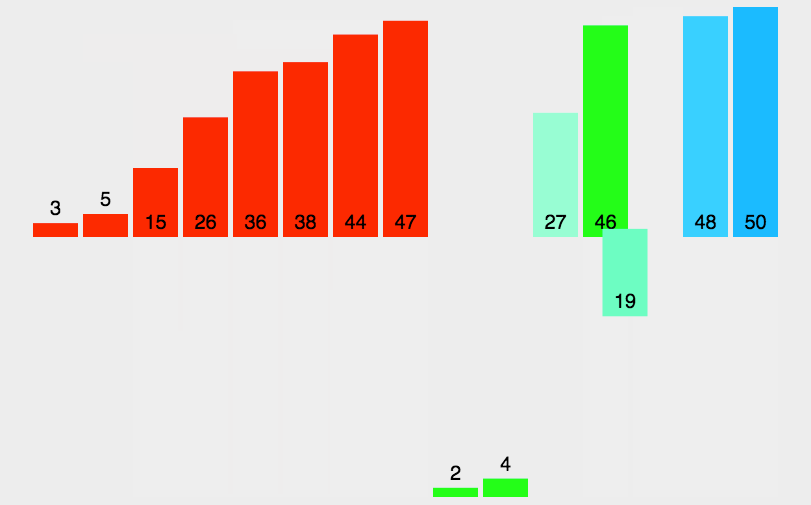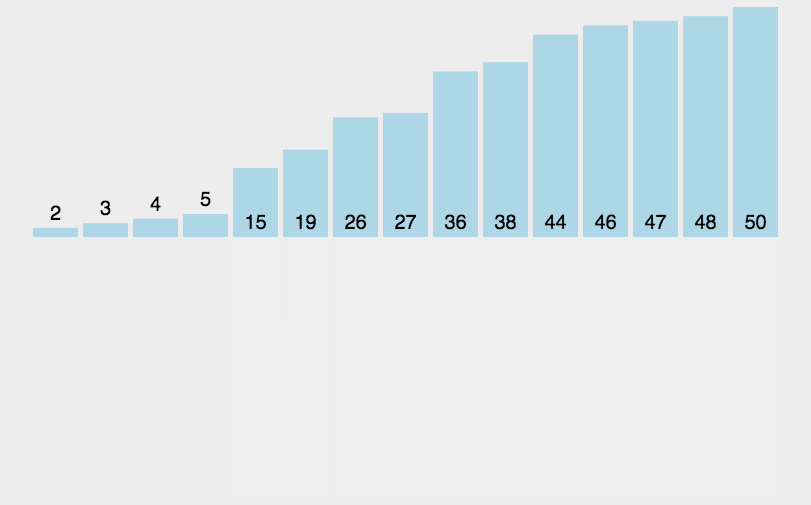
- 程式碼分析:和快速排序類似,歸併排序本身也是一個遞迴的實現,但是也使用了一個
merge方法來重組陣列已排序的部分。merge方法中共有四個迴圈,第一個while迴圈將兩個子列表中的最小元素分別加入到一個臨時的陣列temp中,然後第二個和第三個while迴圈的用處是分別將子列表中剩餘的元素加入到temp中,最後一個for迴圈就是將合併後的資料再複製到原始的陣列中去。
- 時間複雜度分析:每次歸併時要將待排序列表中的所有元素遍歷一遍,因次時間複雜度為O(n)。與快速排序類似,歸併排序也先將列表不斷分割槽直至每個列表只剩餘一個元素,這個過程需要進行log2n次分割槽。因此歸併排序的平均時間複雜度為O(nlogn)。
與之前介紹的五種排序方法不同,基數排序法是一種不需要進行元素之間相互比較的排序方法。
6.基數排序
- 原理:基數排序是基於排序關鍵字結構來排序的,對於關鍵字結構中的每一個數字或者字元,都會建立一個單獨的佇列,而佇列的數目就稱之為基數。而基數排序法究竟是怎麼利用這些佇列的,來看看下面的GIF圖吧:

- 時間複雜度分析:在基數排序中,每一個元素都是不斷從一個佇列中移到另一個佇列中,每次都要進行一次遍歷,時間複雜度為O(n),排序的基數有多大,遍歷就要進行多少次,但基數的大小隻影響n的係數,所以,基數排序的時間複雜度為O(n)。
- 既然基數排序的時間複雜度這麼低,為什麼不是所有的排序都使用基數排序法呢?
- 首先,基數排序無法創造出一個使用於所有物件型別的泛型基數排序,因為在排序過程中要進行關鍵字取值的切分,因此關鍵字的型別必須是確定的。
- 其次,當基數排序中的基數大小與列表中的元素數目非常接近時,基數排序法的實際時間複雜度接近於O(n^2)。
教材學習中的問題和解決過程
- 問題1:為什麼要使用泛型方法?
- 問題1解決方案:如果你定義了一個泛型,不論是類還是介面,那麼Java規定,你不能在靜態方法包括其他所有靜態內容中使用泛型的型別引數。因此,如果想要在靜態方法中使用泛型,就要使用泛型方法了。
public class A<T> {
public static void B(T t) {
//報錯,編譯不通過
}
}- 那麼應該如何定義泛型方法呢?
- 定義泛型方法就像定義泛型類或介面一樣,在定義類名(或者介面名)的時候需要指定作用域中誰是泛型引數。
- 例:
public class A<T> {...} - 表明在類A的作用域中,T是泛型型別引數。
- 例:
- 具體格式是
修飾符 <型別引數列表> 返回型別 方法名(形參列表) {方法體}- 例:
public static <T> int A(List<T> list) { ... }
- 例:
- 泛型方法的定義和普通方法定義不同的地方在於需要在修飾符和返回型別之間加一個泛型型別引數的宣告,表明在這個方法作用域中誰才是泛型型別引數。
- 泛型方法的型別引數可以指定上限,型別上限必須在型別引數宣告的地方定義上限,不能在方法引數中定義上限。規定了上限就只能在規定範圍內指定型別實參,超出這個範圍就會直接編譯報錯。
//正確
<T extends X> void func(List<T> list){ ... }
//正確
<T extends X> void func(T t){ ... }
//編譯錯誤
<T> void func(List<T extends X> list){ ... } - 問題2:在某些書上的某些程式碼中出現的
?是怎麼回事? - 問題2解決方法:
?是一種型別萬用字元,可以代表範圍內任意型別。但是“?”泛型物件是隻讀的,不可修改,因為“?”型別是不確定的,可以代表範圍內任意型別。而所有能用型別萬用字元?解決的問題都能用泛型方法解決,並且泛型方法可以解決的更好。這裡有一篇部落格對於兩者的對比介紹的非常好。 - 問題3:為什麼快速排序法和歸併排序法都要先定義一個私有方法,然後再定義一個公用方法來呼叫私有方法?
- 問題3解決方法:個人理解是因為快速排序法和歸併排序法無法通過只接受陣列物件就可以進行排序,但是為了和其他幾種方法保持一致,所以就先定義了一個私有方法接受陣列物件、最大值和最小值進行排序,然後使用公有方法接受陣列物件,在方法內呼叫私有方法來實現排序。
程式碼除錯中的問題和解決過程
- 問題1:在完成PP9.2的時候,實現的間隔排序無法正確將資料進行排序

程式碼:
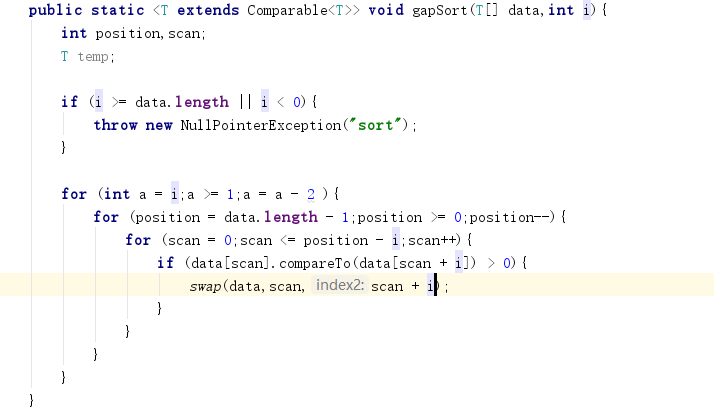
- 問題1解決方法:通過多次測試之後發現,當輸入的數是奇數時排列是正確的,但是當輸入的數是偶數時就不行了。原因是由於我設定的每次的減少了為2,當輸入的數是偶數時,就會少一次迴圈過程,因此我對程式碼進行了修改,增加了對輸入的數進行判斷,如果輸入的是奇數,仍然按原來的方法來,當輸入的是偶數時,每次減少的數量為3。

程式碼託管
上週考試錯題總結(正確為綠色,錯誤為紅色)
- 錯題1:The Java Collections API contains _________ implementations of an indexed list.
- A .Two
- B .Three
- C .Four
- D .Five
- 錯題1解決方法:我本來理解的是Java API中提供了幾種方法來實現列表,因此選擇兩種因為一種是
ArrayList另一種是LinkedList。後來發現是自己看錯題了沒有看到“索引”兩個字,原話在書上120頁。 - 錯題2:The elements of an unordered list are kept in whatever order the client chooses.
- A .True
- B .False
- 錯題2解決方法:當時做題的時候想的是無序列表的順序確實是由使用者來決定的啊,後來想想錯誤可能出在”whatever"上了。
結對及互評
點評模板:
- 部落格中值得學習的或問題:
- 優點:本週的部落格大有長進!內容豐富了很多,終於做到了圖文並茂,值得誇獎!
- 問題:圖片的排版還需加強。
- 程式碼中值得學習的或問題:
- 優點:提了幾周的commit提交終於有所改進,感覺這周我的搭檔有了質的飛躍。
可能是一遍遍的吐槽起了作用,果然像馬原老師說的一樣,量變會引起質變! - 問題:本週程式碼的備註不是很多。
- 優點:提了幾周的commit提交終於有所改進,感覺這周我的搭檔有了質的飛躍。
點評過的同學部落格和程式碼
- 本週結對學習情況
- 20172322
- 結對學習內容
- 給我講解了課堂實驗ASL計算的方法。
- 主要探討了歸併排序的計數方法。
其他(感悟、思考等,可選)
- 因為跳啦啦操的緣故感覺最近的課程總是要落大家一些,現在啦啦操跳完了要趕緊追上大家ヾ(◍°∇°◍)ノ゙
學習進度條
| 程式碼行數(新增/累積) | 部落格量(新增/累積) | 學習時間(新增/累積) | 重要成長 | |
|---|---|---|---|---|
| 目標 | 5000行 | 30篇 | 400小時 | |
| 第一週 | 10/10 | 1/1 | 10/10 | |
| 第二週 | 246/366 | 2/3 | 20/30 | |
| 第三週 | 567/903 | 1/4 | 10/40 | |
| 第四周 | 2346/3294 | 2/6 | 20/60 | |
| 第五週 | 2346/3294 | 2/8 | 30/90 |
計劃學習時間:20小時
實際學習時間:30小時
改進情況:本週的大部分時間基本都花在了對於查詢演算法和排序演算法的理解上了,感覺對時間複雜度理解和計算的應用變得更加熟練了。
