用一行程式碼提升目標檢測準確率

論文摘要

非最大抑制（Non-maximum suppression, NMS）是物體檢測流程中重要的組成部分。它首先基於物體檢測分數產生檢測框，分數最高的檢測框M被選中，其他與被選中檢測框有明顯重疊的檢測框被抑制。該過程被不斷遞迴的應用於其餘檢測框。根據演算法的設計，如果一個物體處於預設的重疊閾值之內，可能會導致檢測不到該待檢測物體。因此，我們提出了Soft-NMS演算法，該連續函式對非最大檢測框的檢測分數進行衰減而非徹底移除。它僅需要對傳統的NMS演算法進行簡單的改動且不增額外的引數。該Soft-NMS演算法在標準資料集PASCAL VOC2007（較R-FCN和Faster-RCNN提升1.7%）和MS-COCO（較R-FCN提升1.3%，較Faster-RCNN提升1.1%）上均有提升。此外，Soft-NMS具有與傳統NMS相同的演算法複雜度，使用高效。Soft-NMS也不需要額外的訓練，並易於實現，它可以輕鬆的被整合到任何物體檢測流程中。

NMS演算法介紹

物體檢測是計算機視覺領域的一個經典問題，它為特定類別的物體產生檢測邊框並對其分類打分。傳統的物體檢測流程常常採用多尺度滑動視窗，根據每個物體類別的前景/背景分數對每個視窗計算其特徵。然而，相鄰視窗往往具有相關的分數，這會增加檢測結果的假陽性。為了避免這樣的問題，人們會採用非最大抑制的方法對檢測結果進行後續處理來得到最終的檢測結果。目前為止，非最大抑制演算法仍然是流行的物體檢測處理演算法並能有效的降低檢測結果的假陽性。

在現有的物體檢測框架（如圖一所示）中，每一個檢測框均會產生檢測分數，那麼對於圖片中的一個物體可能對應多個檢測分數。在這種情況下，除了最正確（檢測分數最高）的一個檢測框，其餘的檢測框均產生假陽性結果。非最大抑制演算法針對特定物體類別分別設定重疊閾值來解決這個問題。

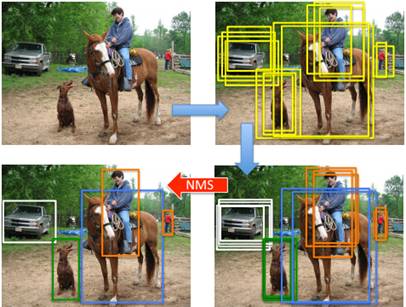
圖一採用NMS的物體檢測流程

傳統的非最大抑制演算法首先在被檢測圖片中產生一系列的檢測框B以及對應的分數S。當選中最大分數的檢測框M，它被從集合B中移出並放入最終檢測結果集合D。於此同時，集合B中任何與檢測框M的重疊部分大於重疊閾值Nt的檢測框也將隨之移除。非最大抑制演算法中的最大問題就是它將相鄰檢測框的分數均強制歸零。在這種情況下，如果一個真實物體在重疊區域出現，則將導致對該物體的檢測失敗並降低了演算法的平均檢測率（average precision, AP）。

換一種思路，如果我們只是通過一個基於與M重疊程度相關的函式來降低相鄰檢測框的分數而非徹底剔除。雖然分數被降低，但相鄰的檢測框仍在物體檢測的序列中。圖二中的例項可以說明這個問題。

圖二被檢測物體高度重疊時，被遮擋物體在不同檢測演算法下具有不同的檢測分數

Soft-NMS可提升目標檢測的平均準確率

針對NMS存在的這個問題，我們提出了一種新的Soft-NMS演算法（圖三），它只需改動一行程式碼即可有效改進傳統貪心NMS演算法。在該演算法中，我們基於重疊部分的大小為相鄰檢測框設定一個衰減函式而非徹底將其分數置為零。簡單來講，如果一個檢測框與M有大部分重疊，它會有很低的分數；而如果檢測框與M只有小部分重疊，那麼它的原有檢測分數不會受太大影響。在標準資料集PASCAL VOC 和 MS-COCO等標準資料集上，Soft-NMS對現有物體檢測演算法在多個重疊物體檢測的平均準確率有顯著的提升。同時，Soft-NMS不需要額外的訓練且易於實現，因此，它很容易被整合到當前的物體檢測流程中。

圖三 Soft-NMS虛擬碼，僅需將NMS程式碼（紅色框）替換為Soft-NMS程式碼（綠色框）一步即可完成

傳統的NMS處理方法可以通過以下的分數重置函式（Rescoring Function）來表達：

在這個公式中， NMS採用了硬閾值來判斷相鄰檢測框是否保留。但是，換一種方法，假設我們對一個與M高度重疊的檢測框bi的檢測分數進行衰減，而非全部抑制。如果檢測框bi中包含不同於M中的物體，那麼在檢測閾值比較低的情況下，該物體並不會錯過檢測。但是，如果bi中並不包含任何物體，即使在衰減過後，bi的分數仍然較高，它還是會產生一個假陽性的結果。因此，在使用NMS做物體檢測處理的時候，需要注意以下幾點：

• 相鄰檢測框的檢測分數應該被降低，從而減少假陽性結果，但是，衰減後的分數仍然應該比明顯的假陽性結果要高。

• 通過較低的NMS重疊閾值來移除所有相鄰檢測框並不是最優解，並且很容易導致錯過被檢測物體，特別是在物體高度重疊的地方

• 當NMS採用一個較高的重疊閾值時，平均準確率可能會相應降低。

Soft-NMS中的分數重置函式

通過衰減與檢測框M有重疊的相鄰檢測框的檢測分數是對NMS演算法的有效改進。越是與M高度重疊的檢測框，越有可能出現假陽性結果，它們的分數衰減應該更嚴重。因此，我們對NMS原有的分數重置函式做如下改進：

當相鄰檢測框與M的重疊度超過重疊閾值Nt後，檢測框的檢測分數呈線性衰減。在這種情況下，與M相鄰很近的檢測框衰減程度很大，而遠離M的檢測框並不受影響。

但是，上述分數重置函式並不是一個連續函式，在重疊程度超過重疊閾值Nt時，該分數重置函式產生突變，從而可能導致檢測結果序列產生大的變動，因此我們更希望找到一個連續的分數重置函式。它對沒有重疊的檢測框的原有檢測分數不產生衰減，同時對高度重疊的檢測框產生大的衰減。綜合考慮這些因素，我們進一步對soft-NMS中的分數重置函式進行了改進：

在圖三的Soft-NMS演算法中，f（iou（M,bi））是基於檢測框重疊程度的權重函式。演算法中每一步的複雜度為O(N)，N為圖片中檢測框的數量。對於N個檢測框，Soft-NMS的演算法複雜度為O（N2），與傳統的貪心NMS演算法相同。由於分數低於一個最小閾值的檢測框會被直接剔除，因此NMS並不需要對所有檢測框進行操作，計算量並不龐大，也不會減慢當前檢測器的執行速度。

值得注意的是，soft-NMS也是一種貪心演算法，並不能保證找到全域性最優的檢測框分數重置。但是，soft-NMS演算法是一種更加通用的非最大抑制演算法，傳統的NMS演算法可以看做是它的一個採用不連續二值權重函式的特例。除了以上這兩種分數重置函式，我們也可以考慮開發其他包含更多引數的分數重置函式，比如Gompertz函式等。但是它們在完成分數重置的過程中增加了額外的引數。

實驗資料分析

我們在兩個標準資料集PASCAL VOC 和MS-COCO上分別進行實驗。Pascal資料集有20種物體分類，MS-COCO資料集含有80種。我們在這裡選擇VOC 2007 測試集來衡量演算法的效能。同時在MS-COCO中一個包含5000張圖片的資料集上完成敏感度分析。此外，我們還在含有20288張圖片的MS-COCO集上展示了結果。為了檢驗我們的演算法，我們在兩種現有的檢測器faster-RCNN和R-FCN上完成實驗。

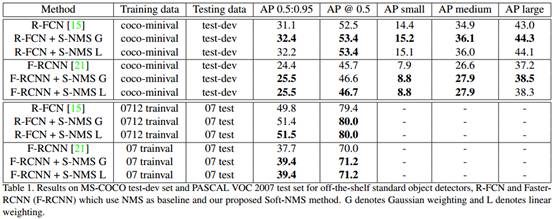
在表一中，我們利用MS-COCO資料集，分別比較了R-FCN和Faster-RCNN演算法在使用傳統NMS和soft-NMS的情況下的效能。我們線上性權重函式中的Nt為0.3，高斯權重函式中Nt為0.5。可以很明顯的看出，Soft-NMS在上述各種情況中均能提高演算法效能，特別是在多物體重疊的情況下。例如，soft-NMS分別使R-FCN和faster-RCNN演算法的平均準確率提升了1.3%和1.1%，在MS-COCO資料集中產生了顯著的提升。值得強調的是，我們只需要對原有NMS演算法做很小的改動便可獲得如此的效能提升。同時，我們也在PASCAL資料集上做了相同的實驗，在表二中，我們可以看到，使用Soft-NMS幫助Faster-RCNN和R-FCN的平均準確率均提升了1.7%。在此之後的實驗，我們均採用高斯權重函式的soft-NMS。

在圖四所示的實驗中，我們可以看到應用soft-NMS的R-FCN演算法在MS-COCO資料集每一類物體識別的準確率均有提升。其中，例如斑馬，長頸鹿，綿羊，大象，馬等動物類物體檢測均有3%到6%的準確率提升。同時，對於麵包機，球類，吹風機等很少多個物體同時出現的類別的物體，平均檢測率提升不明顯。總的來說，Soft-NMS在不影響運算速度的情況下，可以有效的提升物體檢測的成功率。

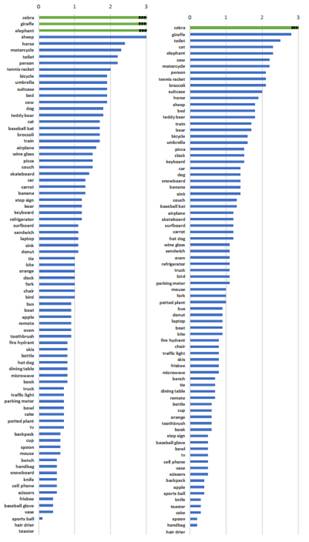
圖四應用於R-FCN（左）和Faster-RCNN（右）的Soft-NMS演算法分類準確率提高

敏感度分析

由上述分析可知，使用Soft-NMS時需要設定引數，使用傳統NMS需要設定引數Nt。為了對這些引數做敏感度分析，我們通過在MS-COCO資料上上不斷改變這些引數的值去觀察平均準確率的變化。如圖五所示，對於兩種檢測器，平均準確率（AP）均在0.3-0.6之間穩定變化，然後在該範圍之外明顯降低。與傳統NMS相比，soft-NMS在0.1-0.7的引數變化範圍內有更好的效能。在0.4-0.7的引數範圍內，使用soft-NMS的兩種檢測器的平均準確率均比傳統NMS大約高1%。儘管在引數為0.6時soft-NMS具有更好的效能，但為了保證實驗的一致性，我們均設定為0.5。

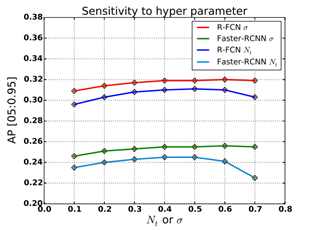
圖五 R-FCN演算法對於引數（Soft-NMS）和Nt（NMS）的敏感度分析

Soft-NMS的定位效果比傳統NMS更精確

定位能力（LocalizationPerformance）：單純適用平均準確率很難表現出soft-NMS在物體檢測效能上的顯著提升。因此，我們需要在不同的重疊閾值下去計算傳統NMS和soft-NMS的平均準確率。同時，我們也在實驗中不斷變化NMS和soft-NMS的引數值來對這兩種演算法有更深入的瞭解。在表三中，隨著NMS重疊閾值Nt的提高，平均準確率降低。儘管在高度重疊（高Ot）的環境下，高重疊閾值Nt有相對好的表現，但是在低Ot環境下，高重疊閾值Nt導致平均準確率AP大幅下降。而soft-NMS 具有不同的特性，在高度重疊（高Ot）環境下取得的好效能在低重疊環境下仍能保持。對於不同的引數設定，soft-NMS均能取得比傳統NMS更好的效能。同時，高可以在高度重疊環境下取得更大的效能提升。因此，相比於傳統NMS，soft-NMS在物體檢測中具有更好的定位效果：

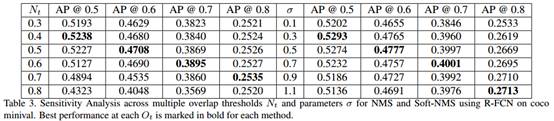
Soft-NMS、NMS的準確度和檢索率對比

最後，我們來觀察在不同重疊閾值的下soft-NMS相對於NMS的效能提升。隨著重疊閾值和檢索率的提升，soft-NMS在準確率上有更大的提升。這是因為傳統NMS對所有重疊區域的檢測框檢測分數均置零，從而錯過了很多待識別物體並導致在高檢索率的情況下準確率降低。Soft-NMS對相鄰區域內的檢測框的分數進行調整而非徹底抑制，從而提高了高檢索率情況下的準確率。與此同時，由於在相鄰區域徹底抑制的NMS在較高重疊環境下更容易錯過待檢測物體，soft-NMS在低檢索率時仍能對物體檢測效能有明顯提升。

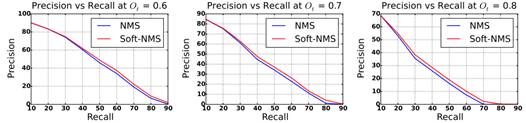
圖六不同物體重疊程度（Ot）下準確度vs 檢索率

定性分析

在圖七中，我們對COCO驗證集中的資料進行了定性分析。其中，我們採用R-FCN來檢測圖片中的物體，檢測閾值為0.45。Soft-NMS在假陽性結果與真實被檢測物體間有少量重疊時對檢測結果有明顯提升。以下圖中8號為例，NMS中使用的一個涵蓋多個人物的較寬的檢測框在soft-NMS中被有效抑制，因為它與圖中多個分數較高的檢測框均有少量重疊，它的檢測分數在分數重置函式的影響下會衰減很多，同樣的情形也在9號圖中出現。在1號的海灘場景中，soft-NMS使得女士包周圍的較大的檢測框被衰減到0.45以下，4號圖中的假陽性結果也同樣被有效抑制。同時，在2,5,7,13號圖中的動物檢測中，NMS對相鄰檢測框產生了過度抑制而soft-NMS通過衰減相鄰檢測框的檢測分數來實現檢測到更多在閾值0.45以上的正確結果。

圖七實驗結果定性分析，圖片對中左圖採用NMS演算法，右圖採用Soft-NMS演算法。藍線以上為檢測成功例項，以下為失敗例項。14號圖檢測物體為人，15號圖檢測物體為長椅，21號圖檢測物體為盆栽。

實驗結論：Soft-NMS在目標檢測中效率更高

本文提出了一種新的軟權重非最大抑制演算法。它通過提供一個基於檢測框重疊程度和檢測分數的函式來實現。作者在傳統貪心NMS演算法的基礎上提出了兩種改進函式並對其在兩個現有檢測資料集上進行了驗證。通過分析，基於檢測框重疊程度和檢測分數的軟權重函式可以有效提升物體檢測的準確率。今後的工作可以考慮從學習更復雜的引數或非引數方程的角度展開。此外，針對物體檢測的端到端的學習框架將是最理想的解決方案，它在生成檢測框時無需考慮非最大抑制以及其中的檢測分數和檢測框位置等多種因素。

論文地址：https://arxiv.org/pdf/1704.04503.pdf

• Github專案：https://github.com/bharatsingh430/soft-nms --------------------- 本文來自 lanyuxuan100 的CSDN 部落格 ，全文地址請點選：https://blog.csdn.net/lanyuxuan100/article/details/78767818?utm_source=copy