【翻譯】Real Shading in Unreal Engine 4
更新至4.20
原文為SIGGRAH2013上Epic Games工程師Brian Karis的分享,雖然現在已經是8102年了,但總體變動不大,依然有學習的價值。

圖1.UE4滲透者Demo
介紹-Introduction
大約在一年前(2012年),我們決定投入一些時間去提升我們的著色模型並且包含一個更加基於物理的材質工作流。它部分驅動自渲染更真實的影象的需求,但是我們也對我們通過更基於物理的方法進行材質建立、使用分層材質可能達到的目標感興趣。藝術家感覺這可能是對工作流和質量的一個巨大的提升,並且我已經在另一個工作室第一時間看到了這些成效,在那裡我們已經過渡到離線混合的材質層。我們的其中一位技術美術在Epic在著色器中做分層的實驗,實現了結果很有希望,這成為了一個額外的需求。
為了支援這個方向,我們知道材質的分層需要簡單,並且高效。迪士尼的演講來的時間十分完美,涉及到了他們的基於物理的著色和使用Wreck-It Ralph的材質模型。Brent Burley 展示了一個非常小的材質引數集合可以足夠精緻的表現離線特性的電影渲染。他童謠展示了一個相當實用的著色模型可以緊密的適用於大多數取樣的材質。他們的工作成為了我們的一個靈感和基礎,並且像他們的“規則”相似,我們也決定去定義一個我們自己的系統的目標。
實時效能-Real-Time Performance
·首要的是,它需要在每次許多可見燈光的條件下高效地使用。
簡化複雜度-Reduced Complexity
·引數儘可能的少。大批的引數不僅會造成決定無力,反覆試驗和錯誤,或者相互關聯的屬性對於一個預期效果需要許多的值來改變。
·我們需要能夠使用基於影象的光照和解析光源可切換,所以引數必須在多有的光照型別中表現一致。
直觀的介面-Intuitive Interface
·我們更傾向易於理解的值,而不是像折射率這樣的物理引數。
感知線性-Perceptually Linear
·我們希望通過蒙版支援分層,但是我們只能承受逐畫素一次著色的負擔。這意味著混合引數著色必須儘可能的匹配著色結果的混合。
簡單掌握-Easy to Master
·我們想要避免需要電介質和導體的技術理解,同時最小化建立基本的貌似物理的材質所需要的努力。
健壯-Robust
·錯誤的建立物理上不可信的材質很困難。
·引數的所有合併應該儘可能的健壯和可信。
善於表現-Expressive
·延遲渲染限制了我們可以使用的著色模型的數量,所以我們的基本著色模型需要足夠描述覆蓋顯示世界中99%的材質。
·所有可分層的材質需要共享相同的引數集在他們中混合。
靈活-Flexible
·其他的專案和授權可能不共享相同的真實感目標,所以也需要足夠靈活來允許非真實感渲染。
著色模型-Shading Model
漫反射雙向反射分佈函式-Diffuse BRDF
我們評估了Burley的漫反射模型但是隻觀察到與Lambertain模型相比輕微的差別(等式1),所以我們不能證明額外的消耗的合理性。除此之外,任何更復雜的漫反射模型很難高效的使用基於影象或球面諧調的光照。因此,我們不在評估其他選擇上投入精力。

這裡Cdiff是材質的漫反射率。
微表面鏡面反射雙向反射分佈函式-Microfacet Specular BRDF
常規的Cook-Torrance微表面鏡面反射著色模型是:
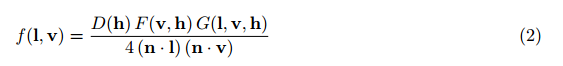
我們開始使用迪士尼的模型,並且評估了比起更高效的替代,每一項的重要性。這遠比聽起來困難;每個項的公佈的公式不一定使用相同的輸入引數,但這對於正確的比較是至關重要的。
鏡面反射D-Specular D
對於法線分佈函式(NDF),我們發現迪士尼選擇的GGX/Trowbridge-Reitz的成本是值得的。對比使用Blinn-Phong的額外消耗相當的小,並且提供了更長的“拖尾”的明顯且自然的表現吸引了我們的藝術家。我們也採用了迪士尼的二次引數化α=Roughness^2。
![]()
鏡面反射G-Specular G
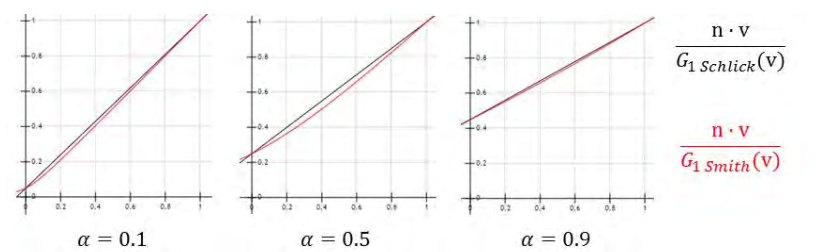
比起其他項,我們對於鏡面反射集合衰減項評估了更多的選擇。最後,我們選擇了Schlick模型,但是令k=α/2,為了更好地適應GGX的Smith模型。應用這個修改,在α=1時Schlick模型恰好匹配Smith,並且在[0,1]範圍內相當的接近近似值(圖2)。我們也選擇去使用迪士尼的修改來降低“熱度”通過在平方前使用(Roughness+1)/2重對映粗糙度。注意到這個調整僅用於解析的光源時很重要的;如果在基於影象的光照中應用,結果會導致在掠射角變得很暗。

鏡面反射F-Specular F
對於菲涅爾,我們做出使用Schlick近似的經典選擇,但是有一點修改,我們使用了球面高斯Spherical Gaussian近似來代替power。這稍微提高了計算效率,並且差異微不可察,公式為:
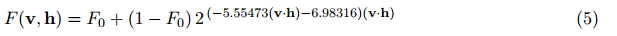
圖2.使用k=α/2的Schlick非常接近Smith匹配
基於影象的光照-Image-Based Lighting
為了在基於影象的光照使用這個著色模型,需要解決輻射率積分,這通常使用重要性取樣來完成。下面的等式描述了這個數值積分:
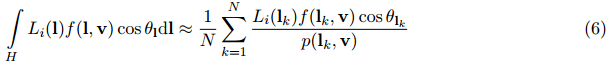
下面的HLSL程式碼展示瞭如何在我們的著色模型中實現(以下與原文略不一致,使用了4.20的程式碼替換):

1 float4 ImportanceSampleGGX( float2 E, float Roughness ) 2 { 3 float m = Roughness * Roughness; 4 float m2 = m * m; 5 6 float Phi = 2 * PI * E.x; 7 float CosTheta = sqrt( (1 - E.y) / ( 1 + (m2 - 1) * E.y ) ); 8 float SinTheta = sqrt( 1 - CosTheta * CosTheta ); 9 10 float3 H; 11 H.x = SinTheta * cos( Phi ); 12 H.y = SinTheta * sin( Phi ); 13 H.z = CosTheta; 14 15 float d = ( CosTheta * m2 - CosTheta ) * CosTheta + 1; 16 float D = m2 / ( PI*d*d ); 17 float PDF = D * CosTheta; 18 19 return float4( H, PDF ); 20 }ImportanceSampleGGX

1 float3 SpecularIBL( uint2 Random, float3 SpecularColor, float Roughness, float3 N, float3 V ) 2 { 3 float3 SpecularLighting = 0; 4 5 const uint NumSamples = 32; 6 for( uint i = 0; i < NumSamples; i++ ) 7 { 8 float2 E = Hammersley( i, NumSamples, Random ); 9 float3 H = TangentToWorld( ImportanceSampleGGX( E, Roughness ).xyz, N ); 10 float3 L = 2 * dot( V, H ) * H - V; 11 12 float NoV = saturate( dot( N, V ) ); 13 float NoL = saturate( dot( N, L ) ); 14 float NoH = saturate( dot( N, H ) ); 15 float VoH = saturate( dot( V, H ) ); 16 17 if( NoL > 0 ) 18 { 19 float3 SampleColor = AmbientCubemap.SampleLevel( AmbientCubemapSampler, L, 0 ).rgb; 20 21 float Vis = Vis_SmithJointApprox( Roughness, NoV, NoL ); 22 float Fc = pow( 1 - VoH, 5 ); 23 float3 F = (1 - Fc) * SpecularColor + Fc; 24 25 // Incident light = SampleColor * NoL 26 // Microfacet specular = D*G*F / (4*NoL*NoV) = D*Vis*F 27 // pdf = D * NoH / (4 * VoH) 28 SpecularLighting += SampleColor * F * ( NoL * Vis * (4 * VoH / NoH) ); 29 } 30 } 31 32 return SpecularLighting / NumSamples; 33 }SpecularIBL
即使有重要性取樣,許多的樣本仍然需要被採集。樣本數量可以通過mip maps顯著的減少,但是數量仍然需要大於16以滿足足夠的數量(原文1024次取樣,4.20為32次取樣)。因為我們對於區域性反射逐畫素的在許多環境貼圖中混合,我們可以只能實際為每一個提供一個樣本。
分離和近似-Split Sum Approximation
為了實現這個,我們通過分離它成為兩項之和來近似以上的和。每一個分離的和可以之後被預計算。對於一個常數Li(l)這個近似是準確的,並且對於常規的環境相當的精確。
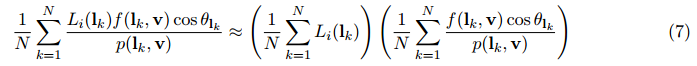
預積分環境貼圖-Pre-Filtered Environment Map
我們對於不同的粗糙度值,預計算第一個和項並且將結果儲存在CubeMap的mip-map層級中。這是在遊戲工業使用的典型方式。一個較小的區別是,我們使用了重要性取樣和我們的著色模型中的GGX分佈對環境貼圖做了卷積。因為這是微表面模型,分佈的形狀改變依賴於到表面上的觀察角度,所以我們假設這個角度是0,例如,n=v=r。各向同性的假設是近似的第二個來源,並且它不幸地意味著我們不會在掠射角獲得漫長的反射。比起分離的和近似,實際上這是我們IBL解決方案中更大的錯誤來源。正如下面程式碼展示的,我們已經發現使用cosθlk可以實現更佳的結果。

1 float3 PrefilterEnvMap( uint2 Random, float Roughness, float3 R ) 2 { 3 float3 FilteredColor = 0; 4 float Weight = 0; 5 6 const uint NumSamples = 64; 7 for( uint i = 0; i < NumSamples; i++ ) 8 { 9 float2 E = Hammersley( i, NumSamples, Random ); 10 float3 H = TangentToWorld( ImportanceSampleGGX( E, Roughness ).xyz, R ); 11 float3 L = 2 * dot( R, H ) * H - R; 12 13 float NoL = saturate( dot( R, L ) ); 14 if( NoL > 0 ) 15 { 16 FilteredColor += AmbientCubemap.SampleLevel( AmbientCubemapSampler, L, 0 ).rgb * NoL; 17 Weight += NoL; 18 } 19 } 20 21 return FilteredColor / max( Weight, 0.001 ); 22 }PrefilterEnvMap
環境雙向反射分佈函式-Environment BRDF
第二個和項包含了剩下的其他所有。這與用一個純白色的環境對鏡面反射雙向反射分佈函式進行積分操作是一樣的,例如,Li(lk)=1。通過Schlick的菲涅爾代替:F(v,h)=F0+(1-F0)(1-v·h)^5,我們發現F0可以因式分解到積分外。
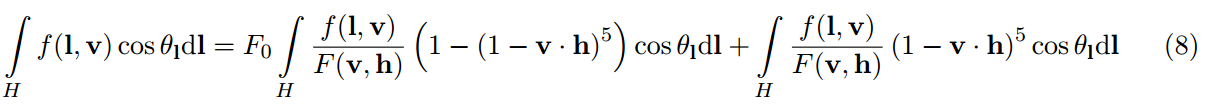
這餘下了兩個輸入(粗糙度Roughness和cosθv),和兩個輸出(F0的縮放和偏移),所有的值都在[0,1]的範圍內。我們預計算這個函式的結果,並且儲存到一個2D的查詢表中。

在完成這項工作之後,我們發現目前的和同時進行的研究,幾乎都是和我們一致的結果。Whilst Gotanda使用了3D查詢表,Drobot優化它到2D的查詢表,就和我們所做的那樣。另外,作為這個課題的一員——Lazarov又向前邁進了一步,展示了相似積分的一對解析近似。

1 float3 IntegrateBRDF( uint2 Random, float Roughness, float NoV ) 2 { 3 float3 V; 4 V.x = sqrt( 1.0f - NoV * NoV ); // sin 5 V.y = 0; 6 V.z = NoV; // cos 7 8 float A = 0; 9 float B = 0; 10 float C = 0; 11 12 const uint NumSamples = 64; 13 for( uint i = 0; i < NumSamples; i++ ) 14 { 15 float2 E = Hammersley( i, NumSamples, Random ); 16 17 { 18 float3 H = ImportanceSampleGGX( E, Roughness ).xyz; 19 float3 L = 2 * dot( V, H ) * H - V; 20 21 float NoL = saturate( L.z ); 22 float NoH = saturate( H.z ); 23 float VoH = saturate( dot( V, H ) ); 24 25 if( NoL > 0 ) 26 { 27 float Vis = Vis_SmithJointApprox( Roughness, NoV, NoL ); 28 29 float a = Square( Roughness ); 30 float a2 = a*a; 31 float Vis_SmithV = NoL * sqrt( NoV * (NoV - NoV * a2) + a2 ); 32 float Vis_SmithL = NoV * sqrt( NoL * (NoL - NoL * a2) + a2 ); 33 //float Vis = 0.5 * rcp( Vis_SmithV + Vis_SmithL ); 34 35 // Incident light = NoL 36 // pdf = D * NoH / (4 * VoH) 37 // NoL * Vis / pdf 38 float NoL_Vis_PDF = NoL * Vis * (4 * VoH / NoH); 39 40 float Fc = pow( 1 - VoH, 5 ); 41 A += (1 - Fc) * NoL_Vis_PDF; 42 B += Fc * NoL_Vis_PDF; 43 } 44 } 45 46 { 47 float3 L = CosineSampleHemisphere( E ).xyz; 48 float3 H = normalize(V + L); 49 50 float NoL = saturate( L.z ); 51 float NoH = saturate( H.z ); 52 float VoH = saturate( dot( V, H ) ); 53 54 float FD90 = ( 0.5 + 2 * VoH * VoH ) * Roughness; 55 float FdV = 1 + (FD90 - 1) * pow( 1 - NoV, 5 ); 56 float FdL = 1 + (FD90 - 1) * pow( 1 - NoL, 5 ); 57 C += FdV * FdL * ( 1 - 0.3333 * Roughness ); 58 } 59 } 60 61 return float3( A, B, C ) / NumSamples; 62 }IntegrateBRDF
最後,為了近似重要性取樣的引用,我們將這兩個預計算的和相乘。

1 float3 ApproximateSpecularIBL( uint2 Random, float3 SpecularColor, float Roughness, float3 N, float3 V ) 2 { 3 // Function replaced with prefiltered environment map sample 4 float3 R = 2 * dot( V, N ) * N - V; 5 float3 PrefilteredColor = PrefilterEnvMap( Random, Roughness, R ); 6 //float3 PrefilteredColor = FilterEnvMap( Random, Roughness, N, V ); 7 8 // Function replaced with 2D texture sample 9 float NoV = saturate( dot( N, V ) ); 10 float2 AB = IntegrateBRDF( Random, Roughness, NoV ).xy; 11 12 return PrefilteredColor * ( SpecularColor * AB.x + AB.y ); 13 }ApproximateSpecularIBL

圖4:最上方為參考,分離和近似位於中間,包含n=v假設的完全近似在最底部。放射對稱性假設引入了最大的錯誤,但是合併近似依然和參考十分近似。

圖5:與圖4相同的對比但是為電介質。
材質模型-Material Mode
我們的材質模式是迪士尼的材質模型的簡化版本,著眼於實時渲染的效率。限制引數的數量對於優化G-Buffer的空間十分重要,減少貼圖的空間佔用和存取,並且最小化在畫素著色器中混合材質圖形的成本。
下面是我們的基礎材質模型:
基本顏色BaseColor 單一顏色。更容易理解的概念
金屬度Metallic 不需要理解電介質和導體的反射率,更少的錯誤空間
粗糙度Roughness 它的概念非常清晰,相反的是光澤度gloss通常需要解釋
凹槽Cavity 用於小規模的遮蔽(實際版本:鏡面反射Specular 用於在非金屬表面上控制鏡面反射量)
Note-Cavity比AO更高頻,通常和AO混合使用,AO是更低頻的資訊,所以這裡Cavity並不是被AO替換,而是Specular。
基本顏色,金屬度,粗糙度都和迪士尼的模型相同,但是溝槽引數沒有介紹,所以它值得解釋。凹槽是用於指定來自小於我們執行時陰影系統可以處理的幾何體遮蔽,通常由於幾何體是在法線貼圖表現的。例如,地板木板間的裂縫和衣服的接縫。
最值得注意的疏忽是鏡面反射引數。我們實際上直到我們的《滲透者》Demo時完成一直在使用它,但最後我們並不喜歡它。首先,我們覺得“鏡面反射”是一個糟糕的引數名稱,造成了很多的誤解並且對於藝術家從控制鏡面反射強度到粗糙度的過渡有負面影響。藝術家和圖形程式一般都忘記他的範圍或者當它的真正預設值是Burley的0.5(對應4%反射率)時,假設預設值為1。在實際使用鏡面反射的情況,幾乎完全是為了小規模的陰影。我們發現可變的折射率(IOR)對於非金屬來說是相對不重要的,所以我們最近用更容易理解的凹槽引數替換了鏡面反射。非金屬的F0現在是常數0.04。(實際版本:引擎中依然使用鏡面反射引數,鏡面反射引數輸入範圍[0,1],預設為0.5,F0的值為鏡面反射引數*0.08。)
以下是來自迪士尼模型中我們沒有選擇採用進我們的基礎材質模型的引數,而是將其作為特例: 次表面Subsurface 陰影貼圖的取樣不同 各向異性Anisotropy 需要更多的IBL樣本 清漆ClearCoat 需要雙倍的IBL樣本 輝光Sheen 在Burley的筆記中沒有很好的定義 *布料Cloth *頭髮Hair *眼睛Eye *雙面植物Two Sided Foliage *預積分面板Preintegrated Skin *次表面輪廓Subsurface Profile (*表示文章沒有提及,但引擎後續更新增加的材質/著色模型) 我們沒有在生產中使用這些特殊的案例模型,除了在我們的《元素》Demo中用於冰的次表面效果。除此之外,我們有一個特別針對面板的著色模型。未來,我們正在考慮採用一種混合延遲/正向著色方法,以更好地支援更專業的著色模型。目前,我們的純延遲著色方法,不同的材質模型使用一個儲存在G-Buffer中的材質模型id的動態分支來處理。經歷-Experiences
有一種情況,到現在我已經見過很多次了。我告訴藝術家要開始過渡到使用不同的粗糙度:“使用粗糙度 ,就像你過去使用的鏡面反射顏色一樣”,不久之後我激動驚喜的聽到:“這行得通!但是一個有趣的評論隨之而來:“粗糙度感覺顛倒了。”事實證明,藝術家們想要看到他們製作的紋理,正如更亮的紋素相當於更亮的鏡面反射高光。如果影象儲存了粗糙度,那麼亮度相當於更高的粗糙度,這將產生低強度的高光。
我收到無數次的一個問題:“金屬度是二進位制嗎?”最初我的解釋是混合或分層材質的微妙之處。但之後我就明白了,最好只說“是的!”原因是,一開始藝術家不願意將引數設定為絕對的;我通常發現金屬的金屬度為0.8。材質分層—接下來進行討論—應該是描述在99%的情況下金屬度不會是0或1。
在過渡期間,我們遇到了一些問題,這些材質是無法再複製的。其中最重要的一些問題來自《堡壘之夜》,這是一款目前在Epic製作的遊戲。《堡壘之夜》有一個非真實感的藝術方向並且對於漫反射和鏡面反射有目的地使用互補色,在我們的新材質模型中是不物理上真實的,而且是故意特意這樣做的。經過長時間的討論,我們決定繼續支援舊的DiffuseColor/SpecularColor作為引擎的開關,以保持《堡壘之夜》的質量,因為它已經開發了很長的時間。然而,我們並不認為新模型排除了非真實感渲染,正如迪斯尼在《無敵破壞王》的使用示範的那樣,我們打算在未來的專案使用它。
材質分層-Material Layering
在我們之前的方法中,共享庫的混合材質圖層提供了許多的好處,這是為了單獨指定材質引數,引數值來自於為每個特殊的模型製作的紋理:
•利用大量資產重新進行工作。
•減少單一資產的複雜度。
•統一併集中了定義遊戲表現的材質,簡易化藝術和技術的方向。
為了完全接受這個新的工作流程,我們需要重新思考我們的工具。從UE3早期開始,虛幻引擎擁有一個特色的基於節點的材質編輯器。這個節點圖指定了輸入(紋理、常量),操作和輸出,它們被編譯成著色器程式碼。
儘管材質分層是這項工作的主要目標,但令人驚訝的是,只需要很小的新增工具層面的需求去支援材質圖層的創作和混合。UE4的材質編輯器的節點圖部分,早已可以被組合為函式,用於多種材質。這種功能是實現材質圖層自然的選擇。把材質圖層放在我們的基於節點的編輯器之中,而不是作為一個之上的固定的函式系統,允許以可程式設計的方式對映和組合圖層。
為了簡化工作流程,我們添加了一個新的資料型別,即材質屬性,它包含了所有的材質輸出資料。這種新型別,像我們的其他型別一樣,可以作為單獨引腳在材質函式中傳入或傳出,通過連線傳遞,並直接輸出。有了這些變化,材質圖層可以和紋理一樣拖進來作為輸入,組合,操作和輸出。事實上,大多數材質圖往往更簡單,因為圖層的採納作為自定義一個特殊材質的主要事情是圖層的對映和混合的。這比過去存在的特定引數操作要簡單得多。
由於有一小部分感性的材質引數,這實際上對圖層用著色器完全混合是可行的。我們認為,在純粹的離線的組合系統它提供了一個實質的質量提高。由於能夠以不同的頻率對映資料,紋理資料的可見解析度可以極高:逐頂點或低頻紋理資料可以是唯一的,混合層遮罩,法線貼圖和溝槽貼圖是逐網格指定的,並且材質圖層是在網格的表面平鋪的。更高階的情況下可能會使用更多的頻率。由於著色器成本,儘管我們事實上限制了我們可以使用的圖層數量,但我們的藝術家還沒有發現限制對他們造成問題。
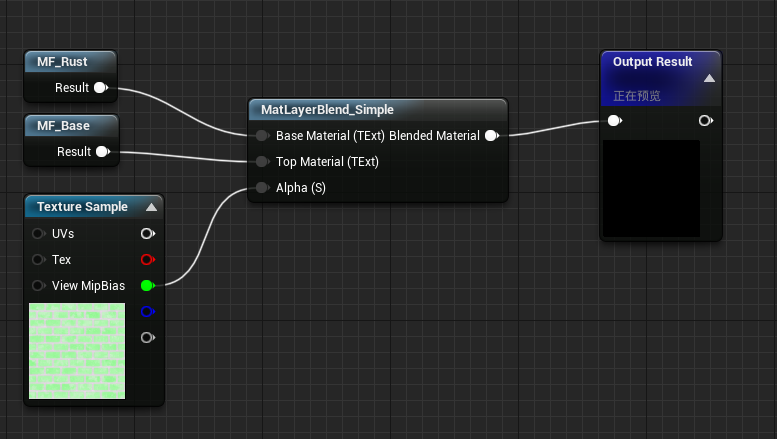
圖6.UE4材質編輯器的簡單材質分層
一個值得關注的方面,案例中,藝術家們通過將一個網格分割成多個部分來解決著色器內的分層限制,導致更多的繪製呼叫。儘管由於CPU方面的程式碼優化,我們希望在UE4中獲得更佳的繪製呼叫數量,這似乎在未來是一個問題來源。一個我們還沒有研究的領域就是使用動態分支在一個層有百分之百覆蓋的區域來減少著色器成本。
到目前為止,我們對材質圖層的經驗是非常積極正面的。我們已經看到了生產效率和質量的大幅提高。我們希望通過簡化查詢和預覽圖層的方式來改進藝術家的材質圖層庫介面。除了我們當前的實時系統之外,我們還打算研究一個離線合成/烘焙系統,以支援更多的層並提供更好的可擴充套件性。

圖7.用鏽跡交換和混合的許多材質圖層

圖8.利用多頻率細節的材質分層結果
光照模型-Lighting Mode
正如著色一樣,我們希望通過使它更基於物理來提高我們的光照模型。我們投入研究的兩個領域是光照衰減和非精確發射源——通常被稱之為面積光源。
提高光照衰減是相當簡單直接的:我們採納了物理精確的反平方衰減並切換到光度學的光通量的亮度單位。這就是說,我們需要解決的一個併發問題是,這種衰減函式沒有值為0時的距離(無窮遠處)。但是為了效率——無論是實時還是離線計算——我們依然需要人工限制燈光的影響。有許多的方式可以實現,但是我們選擇以多數的燈光影響保持相對不受影響的方式去修改反平方函式,同時依然提供了一個柔和到0的過渡。一個比較好的性質是通過修改燈光的半徑不會改變它的有效亮度,這當光照被藝術性的鎖定時很重要,但是因為效能的原因燈光範圍依然需要調整。
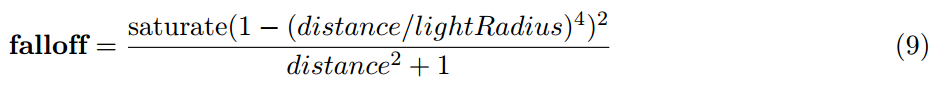
這裡分母中的1是為了防止距離接近光源是函式值爆發。它可以暴露一個藝術家可控制的引數,例如物理矯正不理想的時候。
特別在場景中有許多區域性光源的時候,這個簡單的改變產生的質量差異意味著這很可能是巴克外賣(?)的最大的衝擊。

圖9:反平方衰減實現更自然的結果
面積光照-Area Lights
面積光源不只是生成更真實的影象。當使用基於物理材質的時候他們也相當重要。我們發現沒有這些,藝術家直覺地傾向於避免繪製非常低粗糙度,因為這會導致極小的鏡面反射高光,這看起來並不自然。必要的是,他們盡力去再現製作來自精確光源的面積光照效果。
不幸的是,它的反作用導致了一個著色和光照之間的耦合,打破了基於物理的渲染的核心原則:當用在與他們建立時並不一致的光照環境時,材質不能被修改。
面積光是一個研究的活躍領域。在離線渲染中,常規的解決方案是使用統一取樣或者重要性取樣從光源表面上的許多點處進行照明。對於實時渲染這是完全不實用的。在討論解決方案的可行性之前,這些是我們的需求:
·一致的材質表現
-漫反射BRDF和鏡面反射BRDF評估的能量並沒有明顯的不同。
·當立體角接近0時,接近點光源模型
-我們不想丟失我們的著色模型的任何一方面來實現它。
·足夠快可以在任何地方使用
-否則,我們無法解決上述提及的”偏頗粗糙度“問題。
公告板反射-Billboard Reflections
公告板反射是IBL可以用於離散的光源一種形式。一張儲存了發射光的2D影象,被對映到一個3D空間的矩形。和環境貼圖預過濾相似的是,影象對不同大小的鏡面反射分佈椎體預過濾。計算鏡面反射著色從這個影象中可以被認為作為椎體追蹤的一種形式,這裡一個椎體近似為鏡面反射NDF。椎體中心射線與公告板的平面相交。影象空間的相交點之後被用於紋理座標,並且椎體的半徑在相交處被用於推導一個近似預過濾的mip級別。悲痛的是,影象能以一個直接了當的方式表現十分複雜的面積光源,公告板反射因為多種原因無法滿足我們第二個需求:
·影象是在平面預過濾的,所以在影象空間表現出一個受限制的立體角。
·當射線未於平面相交的時候,沒有資料。
·光照向量,l,是未知的或者假定是反射向量。
椎體相交-Cone Intersection
椎體追蹤不需要預過濾;可以解析地實現。我們試驗過使用Oat的椎體-椎體相交等式追蹤球體上的椎體的一個版本,但是實際操作起來成本過於昂貴。最近,Drobot用一個面向著色點的圓盤與椎體相交提供了一個替代方案。NDF的多項式近似之後在相交區域分段積分。
隨著Drobot最近的進展,這似乎是一個有趣的研究領域。但以目前的形式,它沒有滿足我們的要求。由於是哦那個了一個椎體,鏡面反射分佈必須是徑向對稱地。這就排除了拉伸的高光,微表面鏡面反射模型的一個非常重要的特性。除此之外,像公告板反射,著色模型不需要一個定義的光照向量。
鏡面反射D修改-Specular D Modification
去年,我們展示了基於光源的立體角修改鏡面反射分佈的方法。它的理論是考慮一個光源的分佈與一個對應椎體角D(h)相同。通過增加兩個圓錐體的角度來推匯出一個新的圓錐可以將一個分佈與另一個分佈的卷積近似。為了實現這個,根據等式3轉換α到一個有效的椎體角,加上光源的角度,再轉換回去。α'用於代替α。我們使用下面的近似來實現:

儘管高效,這個技術不幸的是不滿足我們的第一個要求,因為當用大的面積光照亮非常光滑的材質時表現的粗糙。這聽上去顯而易見,但是在鏡面反射NDF簡潔(例如Blinn-Phong)的時候這個技術做的更好,從而更好的匹配光源分佈。對於我們選擇的著色模型(基於GGX),並不可行。

圖10:左邊為參考,右邊是鏡面反射D修改方法。因為在掠射角處失去了球形近似效果很差,並且光滑材質,例如擦亮的黃銅頭盔,看起來粗糙。
代表點-Representative Point
如果對於一個特定的著色點,我們可以將所有來自面積光的光看作來自光源表面的一個單一代表點,我們的著色模型可以直接使用。一個合理的選擇最大貢獻的點。對於一個Phong分佈,就是光源上與反射射線角度最小的點。
這個技術之前已經被髮表,但是能量守恆並沒有解決。通過移動發射光源的原點,我們高效的提高了光源的立體角但是並沒有對額外的能量進行補償。對它的校正比起除以立體角稍微有些複雜,因為能量差異取決於鏡面反射的分佈。例如,改變入射光的方向對於一個粗糙材質會導致很小的能量變化,但是對於一個光滑的材質能量的改變很大。
球形光-Sphere Lights
如果球在地平線之上,球形光的輻照度等於點光。儘管反直覺,這意味著當球落在地平線之下的時候如果我們接受誤差,我們僅僅需要處理鏡面反射光照。我們通過尋找距離射線最小的點近似發現與反射射線之間最小的角度的點。對於一個球這是簡單明瞭的:
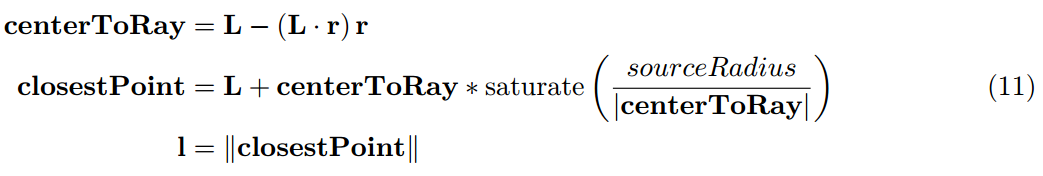
這裡,L是從著色點到光源中心的向量,並且sourceRadius是燈光球體的半徑,r是反射向量。在這個案例中,射線與球相交,計算點將會是射線到球體中心的最近點。一旦標準化,它就是相同的。
通過移動發射光的原點到球的表面,我們通過球的對角高效的拓寬了鏡面反射分佈。儘管它不是一個微表面的分佈,這可以用標準化的Phong分佈來解釋。
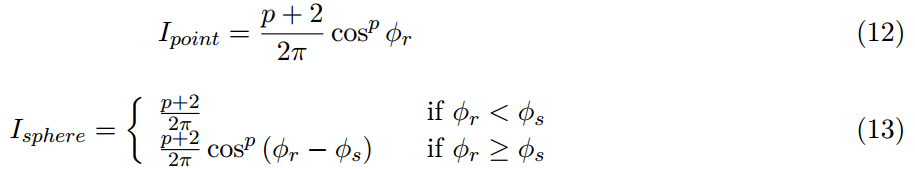
這裡ϕr是r和L之間的夾角,並且ϕs是球對角的半形,Ipoint是標準化的,意味著積分的結果在半球上為1。Isphere顯然不再標準化並取決於p的指數,積分可以大的多。

圖11:用等式13解釋的拓寬效應的視覺化
為了近似能量上的增長,我應用先前描述的鏡面反射修改相同的原由,我們基於光照的立體角拓寬了分佈。我們使用標準化因子實現更廣泛的分佈並替換初始的標準化因子。對於GGX,標準化因子是1/πα2。為了對代表點操作推導一個近似的標準化,我們將新的拓寬的標準化因子除以初始的標準化因子:![]()
代表點方法的結果滿足我們所有的需求。通過正確的處理能量守恆,無論光源大小如何,材質表現一致。光滑材質依然提供了銳利邊緣的鏡面反射高光,並且因為 它只是修改了BRDF的輸入,我們的著色模型不被影響。最後,它足夠高雄啊,允許我們的藝術家再任何地方使用。
燈管-Tube Lights
球形燈對於表現燈泡有幫助,燈管(膠囊)對於表現現實世界中相當廣泛的熒光燈有幫助。開始,我們用一個長度但是半徑為0,也被稱為線性燈光來解決燈管。只要線段再水平線之上,線段的輻照度可以被解析地積分。
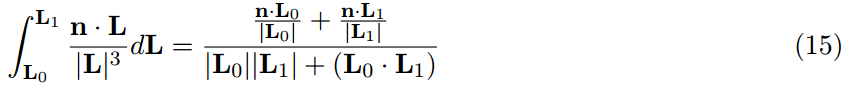
這裡L0和L1是從著色點導線段終點的向量。

圖12:左邊為參考,右邊是代表點方法。儘管能量守恆不完美,我們的近似值與參考值匹配得令人信服。
我們修改了這個方程式來防止輻照度為負值,除以0,並且當長度為0時匹配我們的點光衰減。
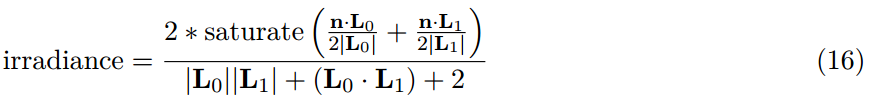
對於線性光鏡面反射我們需要在下面的方程組裡解出t:

Picott發現與r最小角的t的值:
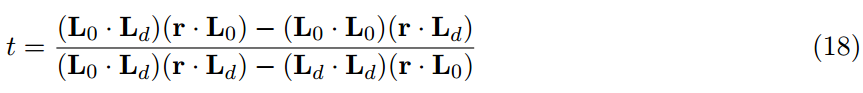
和球的案例相似,我們近似了最小角並且求解而不是為了最短距離:
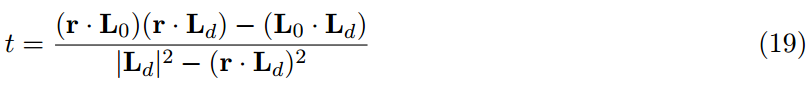
這會造成邊界沒有正常處理的情況,這樣就不能總是找到最近點,但是這樣計算起來成本略低,並且看起來提供了方程式18一樣合理的結果。
注意,這是因為方程式18和19都把r視作一條線段而不是射線是重要的,解決方案都未能正確處理指向遠離線段的射線。甚至對於完美的平面,這會造成從一個結束點到另一個結束點的生硬變化。我們通過在計算點和每一個結束點之間選擇來解決這個問題,但是這樣做成本較高。此時我們只好接受了這個瑕疵。
為了使能量守恆,我們應用了用於球形光的相同概念。鏡面反射分佈通過燈光的對角已經被拓寬,但是這次只是一維的,所以我們使用GGX的各向異性版本。各向異性GGX的標準化因子是1/παxαy,在各向同性案例中,這裡αx=αy=α,這給了我們:
![]()
因為我們只改變了燈光的原點並應用了一個能量守恆項,這些操作可以被加速。用線段和球來做,近似形狀的卷積並且很好的模擬了燈管的表現。燈管的結果展示在圖13。

圖13:使用能量守恆的代表點方法的燈管
我們已經發現能量守恆的代表點方法對於簡單形狀效率高,並且在未來,除了球形和管形之外,可能會應用在其他的形狀。特別是,我們想要應用它到四方紋理來表現更復雜和多彩的光源。
結論
我們在著色,材質和燈光領域轉向基於物理的實現,已經被正式非常的成功。在我們最近的《滲透者》demo的圖形部分貢獻極大,並且我們計劃在未來所有的專案中使用這些實現。事實上,這些改變的可行部分已經整合進《堡壘之夜》,在這項工作開始之前便已經進展順利的專案。我們打算在這些領域以實現更高的靈活性的目的繼續提升,並且提升目標是各種場景和所有級別的硬體可以享受基於物理方法的好處的可擴充套件性。