前面三節，我們從最簡單的一元線性迴歸到多元線性迴歸，討論了，損失函式到底由那幾部分組成（這點我覺很重要，因為它不僅僅存線上性迴歸中還存在其他機器學習中，因此有必要搞明白他，有興趣的請看這篇文章），後面詳細討論了多元線性迴歸，主要介紹了多元線性迴歸的共線性問題，為了解決共線性問題引出了嶺迴歸，然而嶺迴歸存在缺點，因此又引出了lasso演算法，此演算法是解決共線性和選擇特徵很有效的方法（不懂的請看這篇文章），講解了Lasso 演算法的原理，下面就詳解了lasso 的計算原理，通過使用LAR演算法間接解決lasso 的計算問題，他們有很高的相似性，詳解了相似的原因，本人認為LAR演算法值得大家好好研究體會，因為這個演算法使用了很高超的技巧去求解最優問題，計算量很低而且可以推廣到高維特徵，有興趣的請看

先回顧一下簡單的原理過程：

 我們知道了上面的式子就是最優估計了，使用最小二乘法就可以求解出來，但是並不是所有的都可以使用最小二乘法，前提需要保證上式可逆才能使用，

其中和代表的是同一個意思，好，下面我們就開始敲程式碼了：

#!/usr/bin/env/python
# -*- coding: utf-8 -*-
# Author: 趙守風
# File name: regression.py
# Time:2018/11/1
# Email:[email protected]

import numpy as np

# 讀取資料
def loaddataset(filename):
    numfeat = len(open(filename).readline().split('\t')) - 1  # 計算一個樣本特徵有幾個
    datmat = []
    labelmat = []
    fr = open(filename)
    for line in fr.readlines():  # 讀取資料，並把特徵提取出來
        linearr = []
        curline = line.strip().split('\t')
        for i in range(numfeat):
            linearr.append(float(curline[i]))

        datmat.append(linearr)
        labelmat.append(float(curline[-1]))
    return datmat, labelmat

# 求解ws
def standregres(xarr, yarr):
    xmat = np.mat(xarr)
    ymat = np.mat(yarr)
    xTx = xmat.T * xmat
    if np.linalg.det(xTx) == 0.0: #判斷矩陣的行列式是否為0，如果為0說明矩陣不可逆
        print('xTx矩陣不可逆')
        return
    ws = xTx.I * (xmat.T * ymat.T)  # 這裡會報錯,原因是這裡ymat需要轉置一下
    # ws = np.linalg.solve(xTx, xmat*ymat)
    return ws

測試程式碼：
#!/usr/bin/env/python
# -*- coding: utf-8 -*-
# Author: 趙守風
# File name: test.py
# Time:2018/11/1
# Email:
 
[email protected]

import regression
import matplotlib.pyplot as plt
import numpy as np

xarr, yarr = regression.loaddataset('ex0.txt')
print('xarr: ', xarr)
print('yarr: ', yarr)

ws = regression.standregres(xarr, yarr)
print('ws: ', ws)

xmat = np.mat(xarr)
ymat = np.mat(yarr)

plt.scatter(xmat[:,1].flatten().A[0],ymat.T[:,0].flatten().A[0])
plt.show()




fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xmat[:,1].flatten().A[0],ymat.T[:,0].flatten().A[0])
xcopy = xmat.copy()
xcopy.sort(0)
yhat = xcopy* ws
ax.plot(xcopy[:,1],yhat)
plt.show()

 我們發現擬合效果還行，只是沒有把細節的變化表現出來即資料是鋸齒狀上升的，如何把細節表現出來呢？下面使用區域性擬合就可以解決問題。

區域性擬合：

所謂區域性擬合，簡單的來說就是在擬合時，引入權值，是擬合點的相鄰的資料的權值增加，遠離的資料的權值減小或者消除（容易過擬合），其實這個和通訊裡的濾波器差不多，濾波器的目的就是隻讓頻帶內的資料通過，其他的不通過，因此想達到這樣的效果就需要引入權值函式，這個函式和很當前的資料相關，和鄰邊很近的資料也相關，即需要呈現‘帶通’特性，此時最容易想到的就是核函式的高斯核函式或者徑向基核函式具有這樣的特性，如下：

我們的優化函式為：

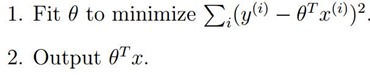
使用這個函式的效果就是我們上面的圖的效果，只是測試細節的變化趨勢忽略了，因此引入區域性擬合即加入權值：

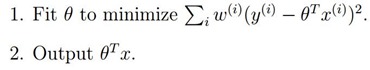
為權值，從上面我們可以看出，如果很大，我們將很難去使得小，所以如果很小，則它所產生的影響也就很小。 

 我們w的權值通過高斯核引入，如下：

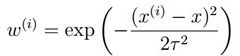
圖形為：

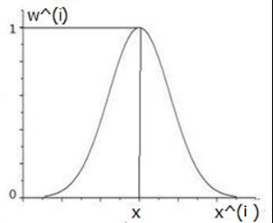
通過這裡我們可以看到，每預測一個待預測樣本資料時 ，靠近x的樣本的資料的權值接近1，而遠離x的權值趨向於0，這就是區域性的意思，就是每加入一個數據，都會以局資料為準進行擬合，這樣就可以把細節也突出了，我們看看，高斯核函式的的特性：

其中k就是上式的，調節 我們發現其選擇臨近資料的多少即權值為多少，可以很清楚的看到，權值可以決定哪些資料參與區域性擬合，因此可以把資料的潛在規律也挖掘出來，但是區域性擬合的缺點是增加了計算量，因為它每預測一個數據時，都會呼叫整個樣本的資料，這和KNN工作機制差不多。好，下面我們看看程式碼實現和效果：

#  區域性線性迴歸
def lwlr(testPoint, xArr, yArr, k=1.0):
    xMat = np.mat(xArr)
    yMat = np.mat(yArr).T
    m = np.shape(xMat)[0] # 取矩陣的行數
    weights = np.mat(np.eye((m))) # 建立一個對角矩陣，對角線為1，其他為0
    for j in range(m):             #next 2 lines create weights matrix
        diffMat = testPoint - xMat[j,:]     # 開始計算權值了
        weights[j,j] = np.exp(diffMat*diffMat.T/(-2.0*k**2))
    xTx = xMat.T * (weights * xMat)
    if np.linalg.det(xTx) == 0.0:
        print("矩陣不可逆")
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

def lwlrTest(testArr,xArr,yArr,k=1.0):  #loops over all the data points and applies lwlr to each one
    m = np.shape(testArr)[0]
    yHat = np.zeros(m)
    for i in range(m):
        yHat[i] = lwlr(testArr[i],xArr,yArr,k)
    return yHat

測試程式碼：

#!/usr/bin/env/python
# -*- coding: utf-8 -*-
# Author: 趙守風
# File name: test.py
# Time:2018/11/1
# Email:[email protected]

import regression
import matplotlib.pyplot as plt
import numpy as np

xarr, yarr = regression.loaddataset('ex0.txt')
print('xarr: ', xarr)
print('yarr: ', yarr)


fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(xmat[:,1].flatten().A[0],ymat.T[:,0].flatten().A[0])
xcopy = xmat.copy()
xcopy.sort(0)
yhat = xcopy* ws
ax.plot(xcopy[:,1],yhat)
plt.show()

yhat1 = regression.lwlrTest(xarr,xarr, yarr, 0.03)
srtind = xmat[:,1].argsort(0)
xsort = xmat[srtind][:, 0, :]
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(xsort[:,1], yhat1[srtind])
ax.scatter(xmat[:,1].flatten().A[0],ymat.T[:,0].flatten().A[0],s=2,c='red')
plt.show()

yhat1 = regression.lwlrTest(xarr,xarr, yarr, 0.01)
srtind = xmat[:,1].argsort(0)
xsort = xmat[srtind][:, 0, :]
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(xsort[:,1], yhat1[srtind])
ax.scatter(xmat[:,1].flatten().A[0],ymat.T[:,0].flatten().A[0],s=2,c='blue')

plt.show()

yhat1 = regression.lwlrTest(xarr,xarr, yarr, 0.005)
srtind = xmat[:,1].argsort(0)
xsort = xmat[srtind][:, 0, :]
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.plot(xsort[:,1], yhat1[srtind])
ax.scatter(xmat[:,1].flatten().A[0],ymat.T[:,0].flatten().A[0],s=2,c='blue')

plt.show()

結果：

我們發現隨著k值的減小，資料的細節特性也表現出來了，尤其在k=0.03時達到最好，而在小以後就出現過擬合了，機器學習實戰好像講反了，實際測試是這樣的，從原理也能解釋，就是說當k越小時，器參與的資料越少，因此更容易過擬合的，好，本節到這裡，下一節繼續討論嶺迴歸和lasso已經LAR演算法的實現。