山東多校聯合模擬賽 Day1
矩形計數(rect)
Description
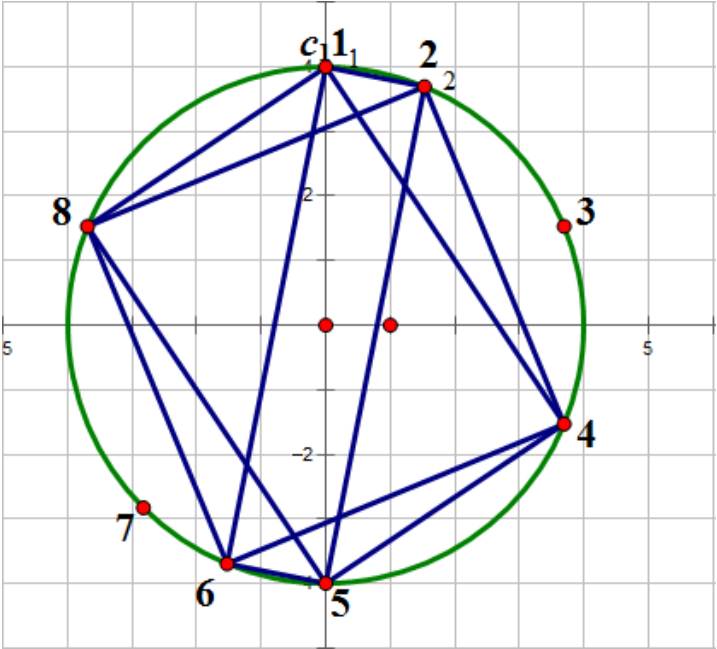
給出圓周上的 \(N\) 個點,請你計算出以這些點中的任意四個為四個角,能構成多少個矩 形。
點的座標是這樣描述的,給定一個數組 \(v[1..N]\),假設圓心為\((0,0)\),圓的周長 \(C=\sum_{i=1}^{N} v_i\) ,第一個點座標為\((0,C/(2π))\)。從第一個點開始,順時針沿圓周走 \(v_1\) 個單位長度, 此時座標為第二個點的座標,再走 \(v_2\) 個單位長度,此時為第三個點的座標,當走完 \(v_1,v_2..v_i\) 個距離後,為第 \(i+1\) 個點的座標(全過程都是沿圓周順時針)。特別的,走完 \(v_1,v_2..v_n\)
個 距離後,就會回到第一個點。Input
輸入檔名為\(rect.in\)
輸入共 \(N+1\) 行。 第一行為正整數 \(N\)。 接下來 \(N\) 行每行一個正整數。其中第 \(i+1\) 行表示的是 \(v_i\)。
Output
輸出檔名為\(rect.out\)
輸出共\(1\) 行,一個整數,表示能構成的矩形的個數。
輸入輸出樣例
\(rect.in\)
8
1
2
2
3
1
1
3
3
\(rect.out\)
3
輸入輸出樣例說明
很明顯的是,圓中的矩形的對角線為圓的直徑.
那麼我們就可以對於圓的直徑搞事情.
表示這個題的樣例解釋和題面對不上(但還是切了 (滑稽
直接計算圓的周長,\(/2\)就是"直徑".(此處由於圓上的距離同樣有\(\pi\),因此這裡忽略\(\pi\))
手玩樣例(觀察)之後,我們發現,只要某一個點與另一個點之間的圓上距離也是\(周長/2\),那它們必然是被直徑連線的.
程式碼
#include<cstdio> #include<iostream> #include<cstdlib> #include<cstring> #include<algorithm> #include<cstring> #include<cctype> #define int long long #define R register using namespace std; inline void in(int &x) { int f=1;x=0;char s=getchar(); while(!isdigit(s)){if(s=='-')f=-1;s=getchar();} while(isdigit(s)){x=x*10+s-'0';s=getchar();} x*=f; } int n,v[280],C,sum[280]; int cnt,dis[280][208]; int pipei[280]; bool ok[280][280]; bool judge(int i,int j) { if(pipei[i] and pipei[j] and !ok[i][j] and !ok[j][i] and !ok[pipei[i]][pipei[j]] and !ok[pipei[j]][pipei[i]]) if(dis[i][j]==dis[pipei[i]][pipei[j]] and pipei[i]!=j and pipei[j]!=i) return true; return false; } signed main() { //freopen("rect.in","r",stdin); //freopen("rect.out","w",stdout); in(n); for(R int i=1;i<=n;i++) in(v[i]),C+=v[i],sum[i+1]=sum[i]+v[i]; if(C&1){puts("0");return 0;} C/=2; for(R int i=1;i<=n;i++) for(R int j=i+1;j<=n;j++) { int x=sum[j]-sum[i]; dis[i][j]=dis[j][i]=x; if(x==C)pipei[i]=j,pipei[j]=i; } for(R int i=1;i<=n;i++) for(R int j=i+1;j<=n;j++) if(judge(i,j)) { cnt++; ok[i][j]=ok[j][i]=ok[pipei[i]][pipei[j]]=ok[pipei[j]][pipei[i]]=1; } printf("%lld",cnt); fclose(stdin); fclose(stdout); return 0; }
祖先(ancestor)
Description
任何一種生物的 DNA 都可以表示為一個由小寫英文字母組成的非空字串。科學家發 現,所有的生物都有可能發生變異。所謂變異,就是子代的 DNA 串與父代的 DNA 串有差 異。每次變異,DNA 串中恰好有一個字元會變成兩個任意的字元。一共有 n 種可能的變異。 變異 ai->bici 表示字元 ai 有可能變異為兩個字元 bici。詳細來說,就是刪掉一個字元 ai,之 後在原來 ai 的位置處,插入 bi,ci 兩個字元(注意字元 bi 必須在 ci 的前面)。每種變異都 有可能發生任意多次。可以發現,每變異一次,DNA 串的長度會加 1。
如果有一種生物 a,他的 DNA 串是 s1,另外存在一種生物 b,他的 DNA 串是 s2。如 果 s2 可以通過若干次變異變為 s1,那麼生物 b 就被叫做生物 a 的祖先。
現在,給定一種生物,他的 DNA 串是 s。請找出他的一個祖先,且這個祖先的 DNA 串 儘量短。
Input
輸入檔案 ancestor.in,共 n+2 行。
第一行包含一個非空字串 s。
第二行含有一個整數 n,表示所有可能的變異。
接下來 n 行,每行描述一種可能的變異,按照 ai->bici 的格式。
s,ai,bi,ci 僅包含小寫英文字母。
請注意:一種變異可能出現多次。
Output
輸出檔名為 ancestor.out。
輸出只有一行,一個整數,表示祖先 DNA 串的最短長度。
發現我們可以將字元兩兩合成,考慮區間\(Dp\)。
由於資料範圍很小.
所以直接暴力預處理.
這裡給出陣列定義,看懂程式碼應該不是很難.
- \(f[i][j][k]\)代表\(i\)到\(j\)能否合成字元\(k\)
- \(dp[i][0]\)代表第\(i\)種變異,替換前的字元.
- \(dp[i][1]\)代表第\(i\)種變異,替換後的第一個字元.
- \(dp[i][2]\)代表第\(i\)種變異,替換後的第二個字元
- \(ans[i][j]\)代表原串\(i\)到\(j\)替換成幾個字元
注意預處理要倒敘,正序會出鍋.(可以手玩一下.
程式碼
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cstring>
#include<cctype>
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
char s[55],ss[55];
bool f[55][55][30];//f[i][j][k]代表從i到j能否為k
int dp[55][3],ans[55][55],len,n;
int main()
{
//freopen("ancestor.in","r",stdin);
//freopen("ancestor.out","w",stdout);
scanf("%s",s+1);len=strlen(s+1);
for(R int i=1;i<=len;i++)f[i][i][s[i]-'a']=true;
in(n);
for(R int i=1;i<=n;i++)
{
scanf("%s",ss+1);
dp[i][0]=ss[1]-'a';
dp[i][1]=ss[4]-'a';
dp[i][2]=ss[5]-'a';
}
// for(R int i=1;i<=n;i++)
// printf("%c->%c%c\n",dp[i][0]+'a',dp[i][1]+'a',dp[i][2]+'a');
for(R int i=len;i>0;i--)
for(R int j=i+1;j<=len;j++)
for(R int k=i;k<j;k++)
for(R int o=1;o<=n;o++)
{
// printf("i:%d j:%d\n",i,j);
if(f[i][k][dp[o][1]] and f[k+1][j][dp[o][2]])
{
// printf("i:%d j:%d %c\n",i,j,dp[o][0]+'a');
f[i][j][dp[o][0]]=1;
}
}
for(R int i=1;i<=len;i++)
for(R int j=i+1;j<=len;j++)
ans[i][j]=2147483647;
for(R int i=len;i>0;--i)
for(R int j=i;j<=len;++j)
{
R bool flg=false;
for(R int k=0;k<26;++k)
if(f[i][j][k])
ans[i][j]=1,flg=true;
if(!flg)
for(R int k=i;k<j;++k)
ans[i][j]=min(ans[i][j],ans[i][k]+ans[k+1][j]);
}
printf("%d",ans[1][len]);
fclose(stdin);
fclose(stdout);
return 0;
}Formula 1(f1)
Description
F1,中文全稱為一級方程式錦標賽,是最高階的方程式賽車比賽,現在你作為一名選 手參加了一場 F1 的比賽,比較特殊地,本次比賽是在一個 N 個點 M 條邊的無向圖上舉行 的。
起點是 S,終點是 T,每條邊長度為 1 公里,賽車每行駛 1 公里耗油 1 個單位,途中共 有 k 個加油站,每經過加油站時,可以把油加滿,但你的賽車設計顧問告訴你,油箱容量越 大,賽車跑的就越慢。為了追求最快的速度,在能順利到達終點,不會中途沒油的前提下, 你希望最小化油箱的容量(注意,雖然油箱變小可能導致路徑變長,但我們只關心最小化的 油箱)。
Input
輸入檔案 f1.in。
第一行一個正整數 T 表示測試資料組數,每組資料格式如下:
第一行三個整數,N,M,K,表示無向圖的點數,邊數,加油站數。
第二行 K 個正整數 i1,i2..ik 表示這些點上有加油站(可能重複,保證至少一個加油站在 S 點)。
接下來 M 行,每行兩個正整數 Bi,Ei 表示有一條連線(Bi,Ei)的雙向邊(可能有重邊和自 環)。
最後一行兩個正整數 S,T 表示起點、終點。
Output
輸出檔名為 f1.out。
對於每組資料,如果沒法到達終點,輸出-1,否則輸出最小化的油箱容量。
二分+\(Spfa\)題,表示第一眼沒看出是二分 emmm(可能是思想太過拘泥了 emm
直接二分油箱容量即可.
這裡\(dis[i]\)代表到達\(i\)的剩餘油量,到達一個加油站要加滿.如果一個點不是加油站且沒油了,直接\(continue\)
程式碼
#include<cstdio>
#include<cstdlib>
#include<cctype>
#include<queue>
#include<cstring>
#define clear(a,b) memset(a,b,sizeof a)
#define N 100008
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int T,n,m,k,dis[N],head[N],tot,s,t;
bool ok[N],vis[N];
struct cod{int u,v;}edge[N<<2];
inline void add(int x,int y)
{
edge[++tot].u=head[x];
edge[tot].v=y;
head[x]=tot;
}
inline bool spfa(int x)
{
for(R int i=1;i<=n;i++)dis[i]=-2147483647,vis[i]=false;
vis[s]=true;dis[s]=x;queue<int>q;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();vis[u]=false;
if(ok[u])dis[u]=x;
if(dis[u]==0)continue;
for(R int i=head[u];i;i=edge[i].u)
{
if(dis[edge[i].v]<dis[u]-1)
{
dis[edge[i].v]=dis[u]-1;
if(ok[edge[i].v])dis[edge[i].v]=x;
if(!vis[edge[i].v])
{
vis[edge[i].v]=true;
/ q.push(edge[i].v);
}
}
}
}
return dis[t]>=0;
}
int main()
{
//freopen("f1.in","r",stdin);
//freopen("f1.out","w",stdout);
in(T);
while(T--)
{
clear(ok,0);clear(head,0);tot=0;
int l=0,r=1e9,ans=214748364;
in(n),in(m),in(k);
for(R int i=1,x;i<=k;i++)in(x),ok[x]=true;
for(R int i=1,x,y;i<=m;i++)
{
in(x),in(y);
add(x,y);add(y,x);
}
in(s),in(t);
while(l<=r)
{
int mid=(l+r)>>1;
if(spfa(mid))r=mid-1,ans=mid;
else l=mid+1;
}
printf("%d\n",ans==214748364?-1:ans);
}
fclose(stdin);
fclose(stdout);
return 0;
}