機器學習基石 Lecture7: The VC Dimension
機器學習基石 Lecture7: The VC Dimension
Definition of VC Dimension
上節課所講的N個樣本分成的dichotomies數量,也就是假設函式種類的數量,的上限
,小於等於上限函式
。而
可以用一個
維的多項式來限制住。這個
叫做Break Point。即:
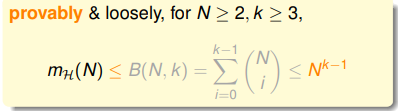
因此VC Bound可以進一步的寫為:

因此只要滿足三點:
- 有Break Point k (好的假設空間 )
- N 足夠大 probably (好的資料集 )
- 演算法 選擇一個錯誤率很小的假設函式作為 probably 能學到東西 (好的演算法 )
對於一個假設空間,
的最大的
叫做這個假設空間的VC 維(VC Dimension)。這個值等於k-1。
下面幾個問題的VC維如圖:

因此,如果VC維是有限大的,那麼就能夠得到一個結果
使得
。與演算法,資料集的取樣分佈以及目標函式都無關。也就保證了機器學習的泛化效能。

VC Dimension of Perceptrons
回顧一下之前的二位PLA演算法。經過了這麼多理論推導,我們終於可以相信演算法最終能夠得到一個比較好的結果。

對於感知機而言,一維形式的感知機的VC維
,二維感知機VC維
,因此假設
維感知機的VC維
。為了證明這一點需要證明兩個不等式:
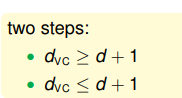
首先證明第一個。要證明VC維大於等於d+1,只需要證明存在任意一個數量為d+1的資料集,能夠被一個假設函式分成
種形式即可。因此我們來設定一個特殊的輸入,每個樣本
的第0位和第i-1位為1,組成輸入矩陣如下:
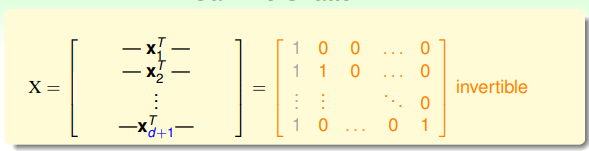
這個矩陣是可逆的。因此對於任意的輸出向量
,對應的係數
都是有解的。而y每一項只有+1和-1兩種選擇,因此存在
種對應的y,也就是存在
種對應的w,即假設函式h。於是得證。
下面證明第二個不等式。需要證明的是對於任意數量為d+2的資料集,都不能夠將對應的結果分類為
種形式。先看一個二維形式下對應的4個數據點的例子:

假設左上右下兩個為正,左下為負。圖中的例子裡不同的
有一個等式。這個等式決定了
對應的點不可能被分為-1。因此大致可以看出
時不同樣本
的線性相關性導致了不能得到
個分類方式。更一般的,對於d維形式的感知機,每個資料點
的維度為
(第一位均為1),因此我們有一個長
寬
的矩陣。根據線性代數的知識,這d+2個向量必然是線性相關的,即
可以寫為其它的
的線性組合的形式。

如果
對應的結果與其係數
的符號相同,這時
的結果必定是+1,也就是說必定缺少了一種結果的分配方式。因此得證。

兩個不等式都證明完畢,因此d維感知機的VC維
。
Physical Intuition of VC Dimension
那麼VC維代表的是什麼物理意義呢?對於每一個假設函式而言我們都有一個不同維度的係數
,改變這個係數向量中的每一維就表示對這個假設函式進行調整。因此這個係數向量表示了假設函式的自由度。而假設空間的數量
類似的表達了這個自由度的概念。而VC維就相當於這些自由度的維度,在多少個有效的維度上改變這些自由度才是有用的。而自由度的維度往往也表示了一個假設函式的擬合目標函式的能力大小。

舉個之前的例子:

很多時候VC維可以近似看成自由係數的個數,當然不完全是。
而在VC bound的不等式中使用了(2N)的VC維指數項代替了M,就會使其面臨與M相似的tradeoff的問題,因此選擇合適的VC維很重要:

Interpreting VC Dimension
VC維可以看成是一種對於模型複雜度的描述。而且在實際應用中會因為複雜度導致一定的penalty。在不等式中可以看到VC維的作用:

當固定了內部錯誤率和外部錯誤率之間的差別
時我們可以看出,越大的VC維就會導致越大的概率上限,有可能會導致這個概率上限大於1而沒有了意義,也就導致了內部錯誤率和外部錯誤率無法再近似相等。
而當我們固定了概率為
時,對應的差別
可以寫為VC維的函式:

因此內部錯誤率和外部錯誤率的差別是VC維的函式,當VC維很大時也會導致它們之間的差別過大不等式無法再起效果。

通常來說,當其它變數保持不變時,VC維與內部錯誤率,外部錯誤率的關係如下圖所示:

那麼我們究竟需要多少個樣本才能夠保證得到一個比較可信的結果呢?根據上限的公式算出來理論的數量是
,但實際使用中
