題目描述

在網友的國度中共有 nnn 種不同面額的貨幣，第 iii 種貨幣的面額為 a[i]a[i]a[i]，你可以假設每一種貨幣都有無窮多張。為了方便，我們把貨幣種數為 nnn、面額陣列為 a[1..n]a[1..n]a[1..n] 的貨幣系統記作 (n,a)(n,a)(n,a)。

在一個完善的貨幣系統中，每一個非負整數的金額 xxx 都應該可以被表示出，即對每一個非負整數 xxx，都存在 nnn 個非負整數 t[i]t[i]t[i] 滿足 a[i]×t[i]a[i] \times t[i]a[i]×t[i] 的和為 xxx。然而， 在網友的國度中，貨幣系統可能是不完善的，即可能存在金額 xxx 不能被該貨幣系統表示出。例如在貨幣系統 n=3n=3n=3, a=[2,5,9]a=[2,5,9]a=[2,5,9] 中，金額 1,31,31,3 就無法被表示出來。

兩個貨幣系統 (n,a)(n,a)(n,a) 和 (m,b)(m,b)(m,b) 是等價的，當且僅當對於任意非負整數 xxx，它要麼均可以被兩個貨幣系統表出，要麼不能被其中任何一個表出。

現在網友們打算簡化一下貨幣系統。他們希望找到一個貨幣系統 (m,b)(m,b)(m,b)，滿足 (m,b)(m,b)(m,b) 與原來的貨幣系統 (n,a)(n,a)(n,a) 等價，且 mmm 儘可能的小。他們希望你來協助完成這個艱鉅的任務：找到最小的 mmm。

輸入輸出格式

輸入檔案的第一行包含一個整數 TTT，表示資料的組數。

接下來按照如下格式分別給出 TTT 組資料。 每組資料的第一行包含一個正整數 nnn。接下來一行包含 nnn 個由空格隔開的正整數 a[i]a[i]a[i]。

輸出檔案共有 TTT 行，對於每組資料，輸出一行一個正整數，表示所有與 (n,a)(n,a)(n,a) 等價的貨幣系統 (m,b)(m,b)(m,b) 中，最小的 mmm。

輸入輸出樣例

2 
4 
3 19 10 6 
5 
11 29 13 19 17 

2   
5  

說明

在第一組資料中，貨幣系統 (2,[3,10])(2, [3,10])(2,[3,10]) 和給出的貨幣系統 (n,a)(n, a)(n,a) 等價，並可以驗證不存在 m<2m < 2m<2 的等價的貨幣系統，因此答案為 222。 在第二組資料中，可以驗證不存在 m<nm < nm<n 的等價的貨幣系統，因此答案為 555。

【資料範圍與約定】

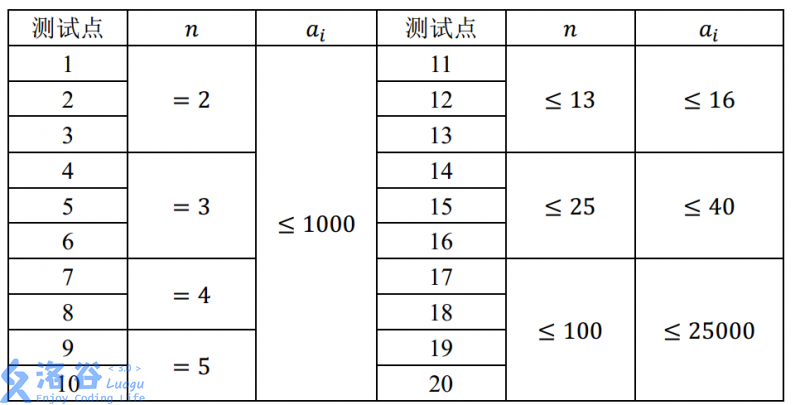
對於 100%100\%100% 的資料，滿足 1≤T≤20,n,a[i]≥11 ≤ T ≤ 20, n,a[i] ≥ 11≤T≤20,n,a[i]≥1。

貪心地排序，那麼問題就等價於如果大的數可以被小的數表示，那麼就可以標記；

我們就可以用完全揹包來做即可；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 400005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
    ll x = 0;
    char c = getchar();
    bool f = false;
    while (!isdigit(c)) {
        if (c == '-') f = true;
        c = getchar();
    }
    while (isdigit(c)) {
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }
    return f ? -x : x;
}

ll gcd(ll a, ll b) {
    return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (!b) {
        x = 1; y = 0; return a;
    }
    ans = exgcd(b, a%b, x, y);
    ll t = x; x = y; y = t - a / b * y;
    return ans;
}
*/



ll qpow(ll a, ll b, ll c) {
    ll ans = 1;
    a = a % c;
    while (b) {
        if (b % 2)ans = ans * a%c;
        b /= 2; a = a * a%c;
    }
    return ans;
}

int T;
int n;
int a[maxn];
int Hash[maxn];

int main()
{
    //ios::sync_with_stdio(0);
    rdint(T);
    while (T--) {
        int ans = 0;
        rdint(n); ms(a); ms(Hash);
        for (int i = 1; i <= n; i++)rdint(a[i]);
        sort(a + 1, a + 1 + n);
        Hash[0] = 1;
        for (int i = 1; i <= n; i++) {
            if (!Hash[a[i]])ans++;
            for (int j = a[i]; j <= 25000; j++)if (Hash[j - a[i]])Hash[j] = 1;
        }
        cout << ans << endl;
    }
    return 0;
}