前言

MRO（Method Resolution Order）：方法解析順序。

Python語言包含了很多優秀的特性，其中多重繼承就是其中之一，但是多重繼承會引發很多問題，比如二義性，Python中一切皆引用，這使得他不會像C++一樣使用虛基類處理基類物件重複的問題，但是如果父類存在同名函式的時候還是會產生二義性，Python中處理這種問題的方法就是MRO。

歷史中的MRO

如果不想了解歷史，只想知道現在的MRO可以直接看最後的C3演算法，不過C3所解決的問題都是歷史遺留問題，瞭解問題，才能解決問題，建議先看歷史中MRO的演化。

Python2.2以前的版本：金典類（classic class）時代

金典類是一種沒有繼承的類，例項型別都是type型別，如果經典類被作為父類，子類呼叫父類的建構函式時會出錯。

這時MRO的方法為DFS（深度優先搜尋（子節點順序：從左到右））。

Class A:   # 是沒有繼承任何父類的
    def __init__(self):
        print "這是金典類"

inspect.getmro（A）可以檢視金典類的MRO順序

import inspect
class D:
    pass

class C(D):
    pass

class B(D):
    pass

class A(B, C):
    
 
pass

if __name__ == '__main__':
    print inspect.getmro(A)
    
(<class __main__.A at 0x10e0e5530>, <class __main__.B at 0x10e0e54c8>, <class __main__.D at 0x10e0e53f8>, <class __main__.C at 0x10e0e5460>)

# 測試用3.6環境測試，
(<class '__main__.A'>, <class '__main__.B'>, <class
 
 '__main__.C'>, <class '__main__.D'>, <class 'object'>)

MRO的DFS順序

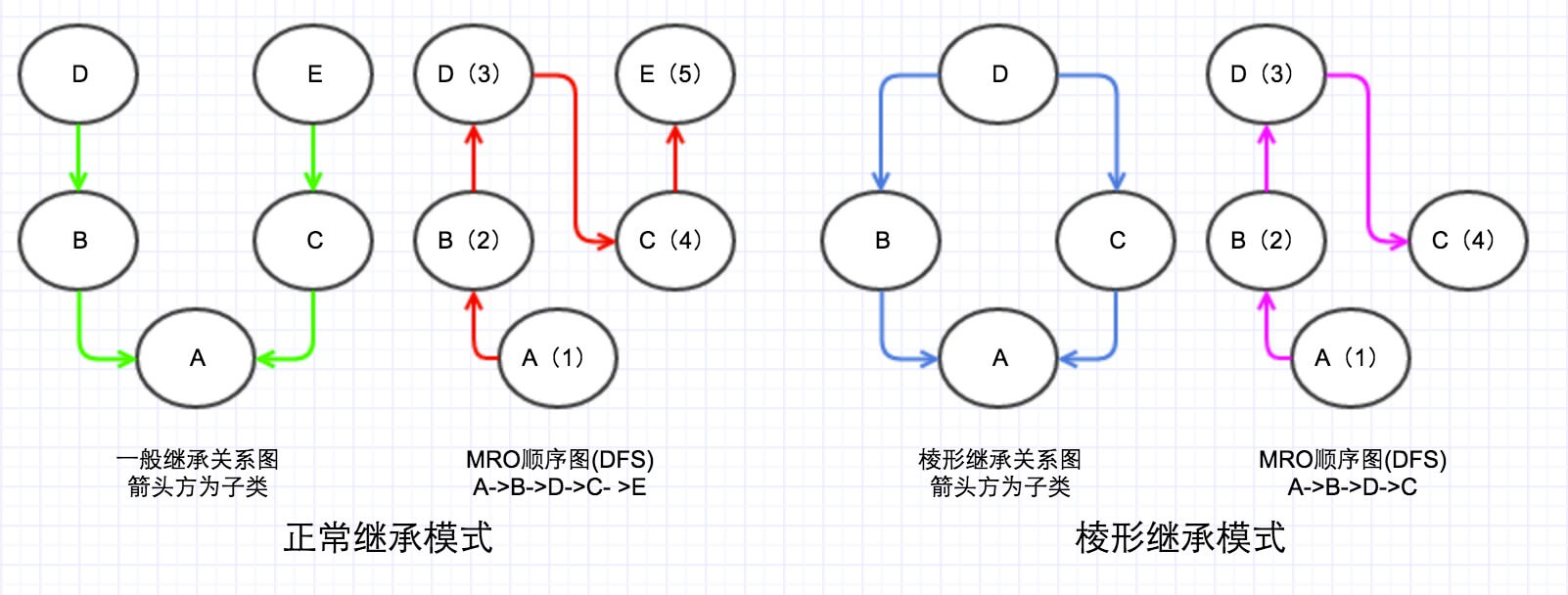
第一種

我稱為正常繼承模式，兩個互不相關的類的多繼承，這種情況DFS順序正常，不會引起任何問題；

第二種

稜形繼承模式，存在公共父類（D）的多繼承（有種D字一族的感覺），這種情況下DFS必定經過公共父類（D），這時候想想，如果這個公共父類（D）有一些初始化屬性或者方法，但是子類（C）又重寫了這些屬性或者方法，那麼按照DFS順序必定是會先找到D的屬性或方法，那麼C的屬性或者方法將永遠訪問不到，導致C只能繼承無法重寫（override）。這也就是為什麼新式類不使用DFS的原因，因為他們都有一個公共的祖先object。

Python2.2版本：新式類（new-style class）誕生

為了使類和內建型別更加統一，引入了新式類。新式類的每個類都繼承於一個基類，可以是自定義類或者其它類，預設承於object。子類可以呼叫父類的建構函式

這時有兩種MRO的方法

1. 如果是金典類MRO為DFS（深度優先搜尋（子節點順序：從左到右））。
2. 如果是新式類MRO為BFS（廣度優先搜尋（子節點順序：從左到右））。

Class A(object):   # 繼承於object
    def __init__(self):
        print ("這是新式類")


A.__mro__ 可以檢視新式類的順序

MRO的BFS順序如下圖：

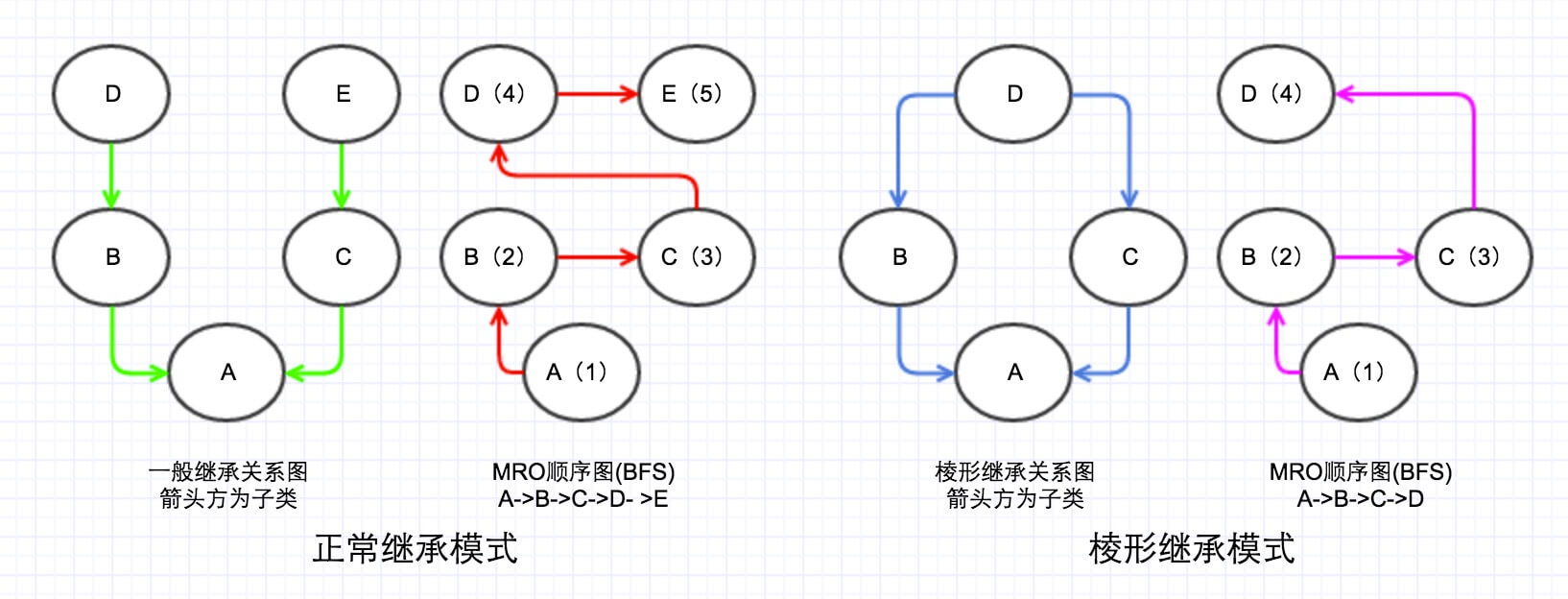
兩種繼承模式在BFS下的優缺點。

第一種

正常繼承模式，看起來正常，不過實際上感覺很彆扭，比如B明明繼承了D的某個屬性（假設為foo），C中也實現了這個屬性foo，那麼BFS明明先訪問B然後再去訪問C，但是為什麼foo這個屬性會是C？這種應該先從B和B的父類開始找的順序，我們稱之為單調性。

第二種

稜形繼承模式，這種模式下面，BFS的查詢順序雖然解了DFS順序下面的稜形問題，但是它也是違背了查詢的單調性。

因為違背了單調性，所以BFS方法只在Python2.2中出現了，在其後版本中用C3演算法取代了BFS。

Python2.3到Python2.7：經典類、新式類和平發展

因為之前的BFS存在較大的問題，所以從Python2.3開始新式類的MRO取而代之的是C3演算法，我們可以知道C3演算法肯定解決了單調性問題，和只能繼承無法重寫的問題。C3演算法具體實現稍後講解。

MRO的C3演算法順序如下圖：看起簡直是DFS和BFS的合體有木有。但是僅僅是看起來像而已。

Python3到至今：新式類一統江湖
Python3開始就只存在新式類了，採用的MRO也依舊是C3演算法。

神奇的演算法C3

C3演算法解決了單調性問題和只能繼承無法重寫問題，在很多技術文章包括官網中的C3演算法，都只有那個merge list的公式法，想看的話網上很多，自己可以查。但是從公式很難理解到解決這個問題的本質。我經過一番思考後，我講講我所理解的C3演算法的本質。如果錯了，希望有人指出來。

假設繼承關係如下(官網的例子)：

class D(object):
    pass
 
class E(object):
    pass
 
class F(object):
    pass
 
class C(D, F):
    pass
 
class B(E, D):
    pass
 
class A(B, C):
    pass
 
if __name__ == '__main__':
    print A.__mro__

首先假設繼承關係是一張圖（事實上也是），我們按類繼承是的順序（class A(B, C)括號裡面的順序B，C），子類指向父類，構一張圖。

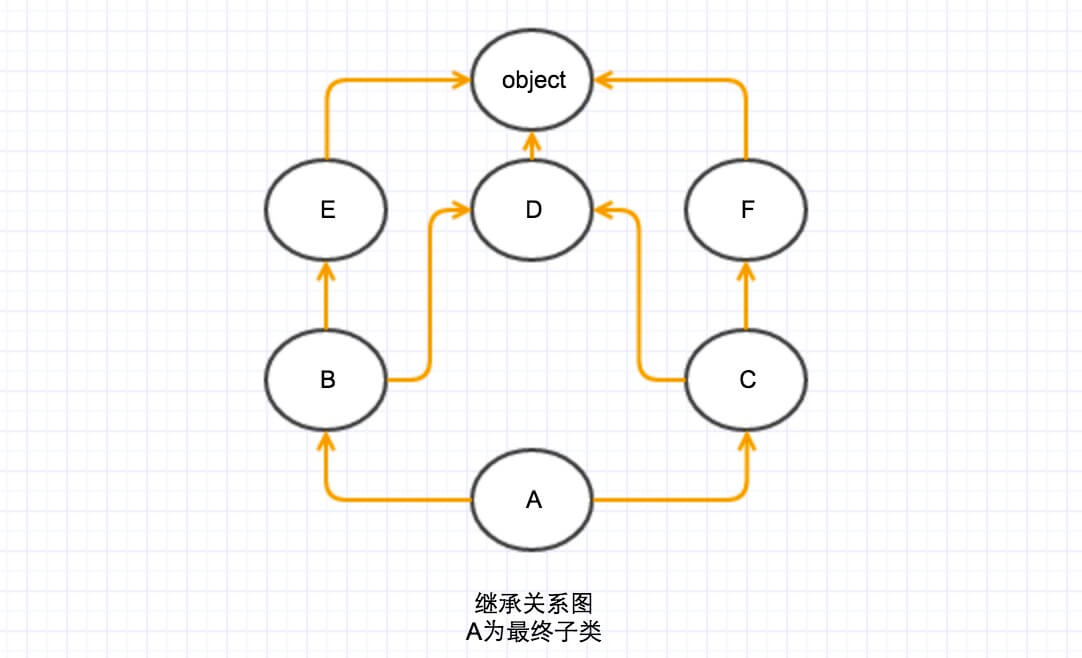
我們要解決兩個問題：單調性問題和不能重寫的問題。
很容易發現要解決單調性，只要保證從根(A)到葉(object)，從左到右的訪問順序即可。
那麼對於只能繼承，不能重寫的問題呢？先分析這個問題的本質原因，主要是因為先訪問了子類的父類導致的。那麼怎麼解決只能先訪問子類再訪問父類的問題呢？如果熟悉圖論的人應該能馬上想到拓撲排序，這裡引用一下百科的的定義:

對一個有向無環圖(Directed Acyclic Graph簡稱DAG)G進行拓撲排序，是將G中所有頂點排成一個線性序列，使得圖中任意一對頂點u和v，若邊(u,v)∈E(G)，則u線上性序列中出現在v之前。通常，這樣的線性序列稱為滿足拓撲次序(Topological Order)的序列，簡稱拓撲序列。簡單的說，由某個集合上的一個偏序得到該集合上的一個全序，這個操作稱之為拓撲排序。

因為拓撲排序肯定是根到葉（也不能說是葉了，因為已經不是樹了），所以只要滿足從左到右，得到的拓撲排序就是結果，關於拓撲排序演算法，大學的資料結構有教，這裡不做講解，不懂的可以自行谷歌或者翻一下書，建議瞭解完演算法再往下看。

那麼模擬一下例子的拓撲排序：首先找入度為0的點，只有一個A，把A拿出來，把A相關的邊剪掉，再找下一個入度為0的點，有兩個點（B,C）,取最左原則，拿B，這是排序是AB，然後剪B相關的邊，這時候入度為0的點有E和C，取最左。這時候排序為ABE，接著剪E相關的邊，這時只有一個點入度為0，那就是C，取C，順序為ABEC。剪C的邊得到兩個入度為0的點（DF），取最左D，順序為ABECD，然後剪D相關的邊，那麼下一個入度為0的就是F，然後是object。那麼最後的排序就為ABECDFobject。

對比一下 A.__mro__的結果

(<class '__main__.A'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <type 'object'>)