案例來自Ross Quinlan的書籍《C4.5：programs for machine learning》
資料集如下

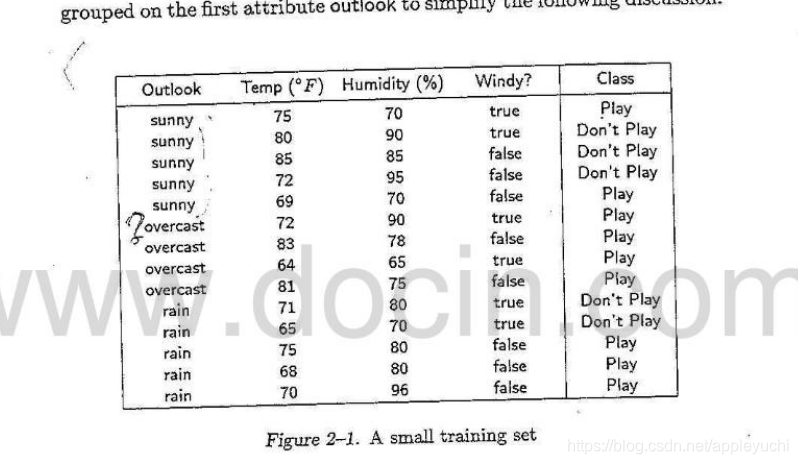
為了模仿缺失值的情況，現在把上面？處的地方改為缺失值。
那麼根據現有13條明確的資料集（不再是14條）
此時
？=sunny的概率是： $\frac{5}{13}$

書中的決策樹如下

上面這個結果是根據下面的原始碼跑出來的。
http://www.rulequest.com/Personal/c4.5r8.tar.gz
對應的決策樹結果是：

繪製上圖對應的程式碼是：
test.dot

digraph graphname {  

        "Outlook"->"Humidity"[label="sunny", fontcolor=darkgreen] // edge T->P  

        "Humidity"->"Play (2.0|0.0)"[label="≤75", fontcolor=darkgreen]
        "Humidity"->"Don't Play (3.4|0.4)"[label="＞75", fontcolor=darkgreen]

        "Outlook"->"Play (3.2|0.0)"[label="overcast", fontcolor=darkgreen]

        "Outlook"->"Windy"[label="rain", fontcolor=darkgreen]

        "Windy"->"Don't Play (2.4|0.4)"[label="true", fontcolor=darkgreen]

        "Windy"->"Play (3.0|0.0)"[label="false", fontcolor=darkgreen]

}
 

執行方法

dot -Tpng -o       decision.png ./test.dot

對於上面的小數解釋如下：

當？=sunny：
該條缺失資料滿足
Outlook=sunny
Humidity>75
也就是說到達了Don’t Play這個葉子節點，但是該資料是屬於Play這個類別的
所以加上原來的3條資料，總共是 $3\frac{5}{13}$條資料，由於類別與該類別不一致，所以該葉子節點的誤判條數為 $\frac{5}{13}$條
所以該葉子節點的最終結果是：（ $3\frac{5}{13}$| $\frac{5}{13}$）=(3.4|0.4)
表示到達該葉子節點的有 $3\frac{5}{13}$條，其中不滿足的有 $\frac{5}{13}$條

當？=overcast：由於13條資料中有3條資料是overcast，所以概率是 $\frac{3}{13}$
由於滿足Outlook=overcast的資料全部屬於Play，而該缺失資料也屬於Play，
所以不存在誤判
該葉子節點最終到達資料共計 $3\frac{3}{13}$條，誤判0.0條
所以該葉子節點的最終結果是：（ $3\frac{3}{13}$|0.0）=(3.2|0)